Кинематика и динамика материальной точки

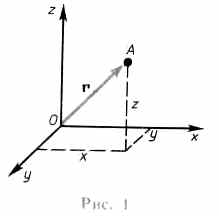
1. Положение материальной точки опре­деляется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета — совокупность системы координат и часов, связанных с телом отсчета. В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент вре­мени по отношению к этой системе характеризуется тремя координатами х, у и z или радиусом-вектором r, проведен­ным из начала системы координат в дан­ную точку. Число независимых координат, полно­стью определяющих положение точки в пространстве, называется числом степе­ней свободы. Если материальная точка свободно движется в пространстве, то она обладает тремя степенями свободы (х, у и z); если она движется по плоскости, то - двумя степенями свободы, ес­ли движется вдоль некоторой линии, то - одной степенью свободы.

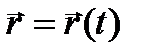При движении материальной точки ее координаты с течением времени изменяют­ся. В общем случае ее движение определя­ется скалярными уравнениями , эквивалентными векторному уравнению . Это - кинематические уравнения­ движения материальной точки. Траекто­рия движения материальной точки — ли­ния, описываемая этой точкой в простран­стве относительно выбранной системы отсчета. Вид траектории зависит от характера движения материальной точки и от системы отсчета.

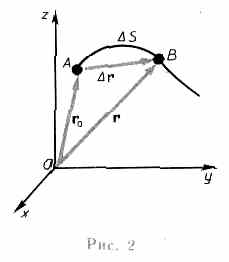
Длина участка траектории, прой­денного материальной точкой с момента начала отсчета времени, называется дли­ной пути s и является скалярной фун­кцией времени: Ds = Ds(t). Вектор 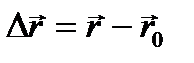, проведенный из начального положе­ния движущейся точки в положение ее в данный момент времени (приращение радиус-вектора точки за рассматривае­мый промежуток времени), называется пе­ремещением.При прямолинейном движении 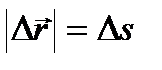Поступа­тельное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллель­ной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

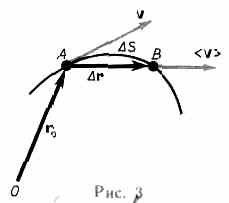
СКОРОСТЬ – векторная величина, которой определяется как быстрота движения, так и его направление в данный момент времени. Вектор средней скорости - отношение приращения радиуса-вектора точки к промежутку времени: . Направление вектора средней скоро­сти совпадает с направлением Dr. Мгновенная скорость - векторная величина, равная первой производной радиуса-вектора движущей­ся точки по времени. 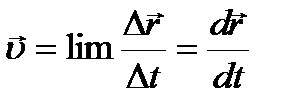Вектор мгновенной скорости направлен по касатель­ной к траектории в сторону движения. Модуль мгновенной скорости 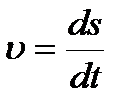равен первой производной пути по времени. Средняя ско­рость неравномерного движения 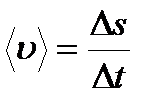Единица скорости – 1 метр в секунду – скорость прямолинейно и равномерно движущейся точки, при которой эта точка за 1 с перемещается на расстояние 1 м. 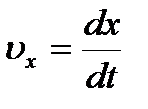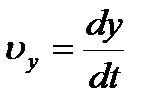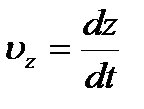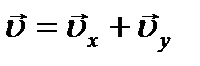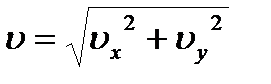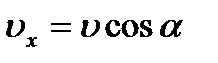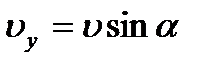Проекции вектора скорости на оси координат ; ; Движение в одной плоскости описывается уравнениями: 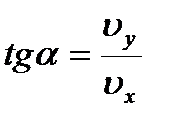, где 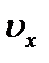, 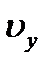- проекции вектора скорости на оси координат. Движение точки в пространстве

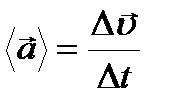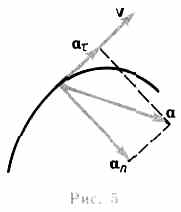
Ускорение - характеристика неравномерного движения, определяющая быстроту изменения скорости по модулю и направлению. Единица ускорения – метр на секунду в квадрате – ускорение прямолинейного ускоренного движения точки, при котором за 1 с скорость точки изменяется на 1м/с. Среднее ускорение - векторная величина, равная от­ношению изменения скорости к интер­валу времени Мгновенное ускорение - вектор­ная величина, равная первой производной скорости по времени 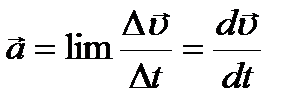Тангенциальная составляющая уско­рения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории). Она равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю 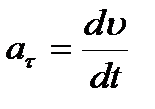. Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена по нормали к траектории, центру кривизны, поэтому называют центростремительным ускорением) 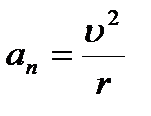. Полное ускорение - геометри­ческая сумма тангенциальной и нормальной: 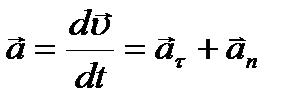. Модуль полного ускорения Вычисление пройденного пути 1. Путь, пройденный точкой за промежуток времени от t₁ до t₂ 2. Путь, пройденный точкой за время t при равномерном движении 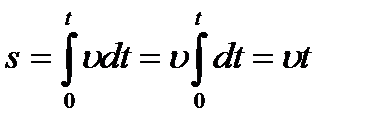3. Путь, пройденный точкой за время t при равноускоренном движении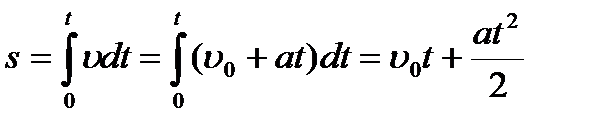

2. Элементы кинематики вращательного движения. Угловая скорость - вектор­ная величина, равная первой производной угла поворота тела по времени: 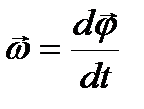. Вектор угловой скорости направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dj. Единица измерения угловой скорости - радиан в секунду (рад/с). Линейная скорость точки 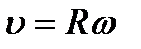. Эту же формулу можно записать как вектор­ное произведение: , при этом модуль вектора линейной скорости равен 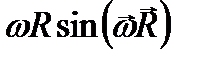, а направление вектора линейной скорости совпадает с направлением поступательного движения правого винта при его вращении от w к R. Перио­д- время, за которое точка поворачивается на угол 2p: 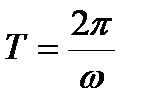Частота вращения - число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени: 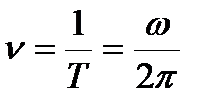Угловое ускорение - векторная величина, равная первой производ­ной угловой скорости по времени Направление вектора углового ускорения: при ускоренном движении вектор углового ускорения сонаправлен вектору угловой скорости, при замедленном - противонаправлен ему. Тангенциальная составляющая 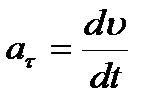или Нормальная составляющая ускорения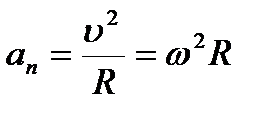

Для равнопеременного движения точки по окружност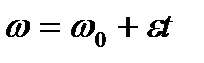и и

3. Динамика является основным разделом механики, в ее основе лежат три закона Ньютона, сформулированные им в 1687 г. Законы Ньютона играют исключительную роль в механике и являются обобщени­ем результатов огромного человеческого опыта. Их рассматривают как систему взаимосвязанных законов и опытной про­верке подвергают не каждый отдельный закон, а всю систему в целом.

Первый закон Ньютона: всякая мате­риальная точка (тело) сохраняет состоя­ние покоя или равномерного прямолиней­ного движения до тех пор, пока воздейст­вие со стороны других тел не заставит ее изменить это состояние.

Масса тела — физическая величина, являющаяся одной из основных характе­ристик материи, определяющая ее инерци­онные свойства. Масса обладает свойством аддитивности.

Сила — это векторная величина, являюща­яся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. Сила характеризуется: точкой приложения, модулем и направлением. Единица силы в СИ — ньютон (Н): 1 Н есть сила, которая массе 1 кг сообща­ет ускорение 1 м/с² в направлении дейст­вия силы: 1 Н = 1 кг•м/с²

Второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорцио­нально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точ­ки (тела).

,

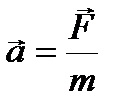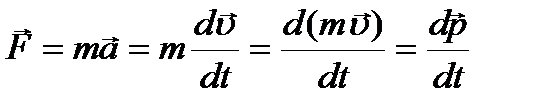
Векторная величина 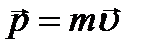, численно равная произведению массы ма­териальной точки на ее скорость и име­ющая направление скорости, называется импульсом этой материальной точки.

Более общая формули­ровка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе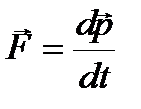

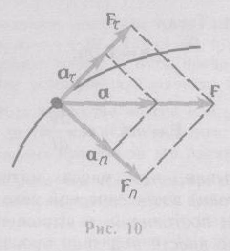
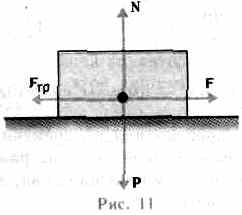
Принцип независимости действия сил: если на материальную точку действует одно­временно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускоре­ния можно разлагать на составляющие, использование которых приводит к су­щественному упрощению решения задач. Например, на рис. 10 действующая сила F = ma разложена на два компонента: тангенциальную силу F_t (направлена по касательной к траектории) и нормальную силу F_n (направлена по нормали к центру кривизны).

,

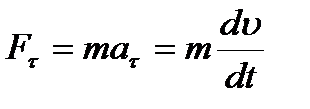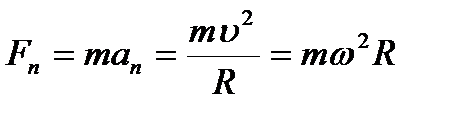
Третий закон Ньютона: силы, с которы­ми действуют друг на друга материальные точки, всегда равны по модулю, противо­положно направлены и действуют вдоль прямой, соединяющей эти точки: , где F₁₂ — сила, действующая на первую материальную точку со стороны второй; F₂₁ — сила, действующая на вторую мате­риальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

И.Ньютон, изучая дви­жение небесных тел, на основании законов Кеплера и основных законов динамики открыл всеобщий закон всемирного тя­готения: между любыми двумя материаль­ными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек и обратно пропорциональная квадрату расстояния между ними: 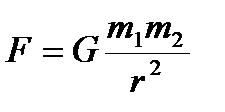Эта сила называется гравитационной (или силой всемирного тяготения). Силы тяго­тения всегда являются силами притяже­ния и направлены вдоль прямой, проходя­щей через взаимодействующие тела. Коэффициент пропорциональности G на­зывается гравитационной постоянной, G=6,67•10^-11Н•м²/кг². Закон всемирного тяготения установ­лен для тел, принимаемых за материальные точки.

Вес - сила, с которой тело вследствие тяготения к Земле действует на опору (или подвес). Вес тела проявляется только в том случае, если тело движется с ускорением, отличным от g, т. е. когда на тело, кроме силы тяжести, действуют другие силы. Состояние тела, при котором оно движется только под действием силы тяжести, на­зывается состоянием невесомости. Гравитационное взаимодействие меж­ду телами осуществляется с помощью поля тяготения, или гравитационного поля. Это поле порождается телами и является формой существования материи. Основное свойство поля тяготения заключается в том, что на всякое тело массой m, вне­сенное в это поле, действует сила тяготе­ния, т. е. 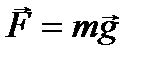. Вектор g не зависит от m и называется напряженностью поля тяготения. Напря­женность поля тяготения определяется си­лой, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действую­щей силой. Напряженность есть силовая характеристика поля тяготения.

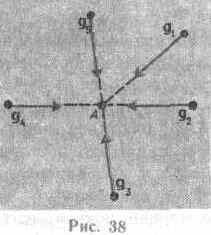
Поле тяготения называется однород­ным, если его напряженность во всех точ­ках одинакова, и центральным, если во всех точках поля векторы напряженности направлены вдоль прямых, которые пере­секаются в одной точке, неподвижной по отношению к какой-либо инерциальной системе отсчета (рис.38). Для графического изображения сило­вого поля используются силовые линии (линии напряженности). Потенциал поля тяготения j — ска­лярная величина, энергетическая характери­стика поля тяготения, определяемая потенци­альной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точ­ки поля в бесконечность .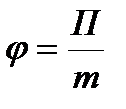

Внешнее трение - трение, возникающее в плоскости касания двух соприкасающих­ся тел при их относительном перемещении. Внешнее трение обусловлено шероховатостью соприкасающихся повер­хностей; в случае же очень гладких по­верхностей трение обусловлено силами межмолекулярного притяжения. Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения или качения. Внутреннее трение - тре­ние между частями одного и того же тела, например между различными слоями жид­кости или газа, скорости которых меняют­ся от слоя к слою. В отличие от внешнего трения здесь отсутствует трение покоя. Сила трения скольжения F_тр пропорциональна силе N нормального давления, с которой одно тело действует на другое 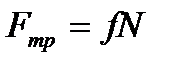, где f — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей. Он ра­вен тангенсу угла a₀, при котором на­чинается скольжение тела по наклонной плоскости. Закон трения скольжения 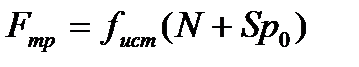, где p₀ — добавочное давление, обус­ловленное силами межмолекулярного при­тяжения, которые быстро уменьшаются с увеличением расстояния между частица­ми; S — площадь контакта между телами; f_ист — истинный коэффициент трения скольжения. Сила трения качения определяется по закону Кулона 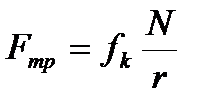, где r — радиус катящегося тела; f_k — коэффициент трения качения, измеряемый в метрах.