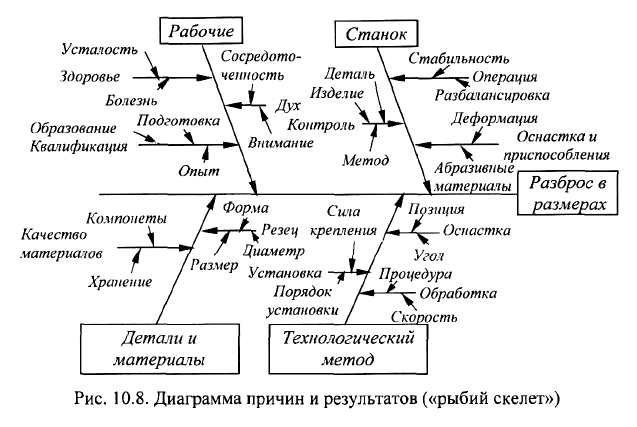
Диаграммы причин и результатов

Выявление дефекта изделия повышает качество конечной продукции, но не

исключает повторения брака на других деталях и изделиях. Для снижения

издержек производства важно исключить причины, приводящие к браку. Но

для этого сначала надо эти причины выявить. Диаграмма причин и результатов,

часто называемаядиаграммой Исикавы, позволяет выразить цепь причин и

результатов в простой и доступной форме. Японский профессор К.Исикава

первым в мировой практике применил диаграмму, показывающую отношение

между показателем качества и воздействующими на него факторами. Диаграмму

причин и результатов часто на практике называют диаграммой «рыбий скелет»

или диаграммой «речных притоков».

Как построить диаграмму причин и результатов? На первом этапе следует

выбрать показатель качества, причины снижения которого надо определить.

Допустим, что это какой-то контролируемый размер детали, часто выходящий за

пределы установленного допуска. Этап 2 - провести в середине чистого листа

бумаги горизонтальную линию и в конце ее записать анализируемый показатель

качества. Назовем горизонтальную линию «хребтом» диаграммы. Этап 3 -

провести под углом, близким к прямому, наклонные линии к «хребту» в виде

стрелок, на концах которых написать главные причины, которые, по вашему

мнению, могут влиять на изменение показателя качества (рис. 10.8). Назовем эти

стрелки «большими костями хребта». Этап 4 - провести к «большим костям»

горизонтальные линии («средние кости»), на которых написать причины

(вторичные), влияющие на главные причины. Этап 5 - если можно допустить

наличие причин (третичного порядка), которые влияют на вторичные причины, то

необходимо провести наклонные стрелки («мелкие кости») к «средним костям» и

надписать причины. Этап 6 - проранжировать причины по значимости и

выделить особо важные, которые предположительно оказывают наибольшее

влияние на показатель качества. Обвести названия этих причин двойными

линиями.

Анализ

Диаграммы.

После

построения

диаграммы

и

выделения

предполагаемых причин необходимо провести измерения показателя качества и

выделить группы данных по каждой рассматриваемой причине. Например, если

вы допустили, что виноваты или рабочий, или резец, или станок, то необходимо

провести проверки с этим (исследуемым) станком и другим (контрольным), с

этим резцом и контрольным, этим рабочим и контрольным.

Желательно провести проверки в течение определенного периода, за

который, например, может затупиться резец, или потеряет наладку станок, или

устанет рабочий и т.д. Очень важно проанализировать, какие изменения на этом

рабочем месте произошли в последнее время. Например, отремонтировали станок,

сменили материал резцов, приняли нового рабочего для заточки резцов, поменяли

техпроцесс изготовления детали и т.д. Исследуя отношения между показателем

качества и «большими костями», между «большими» и «средними», а также

между «средними» и «мелкими костями», можно логическим путем построить

полезную диаграмму причин и результатов. С накоплением опыта анализа процесс

отыскания истинных причин значительно сокращается. В процесс анализа

целесообразно

вовлечь

как

можно

больше

работников,

занятых

в

производственном процессе или обслуживающих его. Этот мозговой штурм

может значительно приблизить исследователей к обнаружению и проверке ис-

тинной причины разброса показателя качества. При длительных безуспешных

поисках причины разброса целесообразно вернуться к диаграмме и снова опре-

делить, все ли возможные причины нашли отражение на диаграмме.

После выявления и устранения причин желательно повторить построение

диаграммы Парето и сравнить ее с первоначальной. Процесс поиска можно

считать законченным, если издержки производства по данному показателю ка-

чества снизились в 2 - 5 раз.

Гистограммы

Рассеяние,

Генеральные

Совокупности

и

Выборки.

Параметры

технологического процесса, на которые действуют множество факторов (человек,

оборудование, режущий инструмент, материал, температура окружающей среды и

т.д.), не могут быть все время одинаковы и изменяются в пределах, влияющих на

них погрешностей действующих факторов. Так что неизбежно, что в любом

заданном множестве значений параметра будетрассеивание. Но, хотя сами

значения параметра все время меняются, они подчиняются определенной

закономерности, которую называютраспределением.

При контроле качества изделий необходимо на основе собранных данных

выявить реальное состояние показателей качества изделия, по которым, сравнивая

их с требуемыми показателями, принимается окончательное решение о годности

данного изделия. Если проверяются все изделия, то вся их совокупность называется

генеральной популяцией илигенеральной совокупностью. Одно или несколько

изделий, взятых из генеральной совокупности, называетсявыборкой. Так как

выборка

используется

для

оценивания

характеристик

всей

генеральной

совокупности, ее необходимо выбирать таким образом, чтобы она отражала именно

эти характеристики. А для этого выборка должна быть случайной. Данные,

полученные на выборках, служат основой для решения о генеральной совокупности.

Очевидно, что чем больше объем выборки, тем больше информации об этой

совокупности можно получить, тем точнее она будет характеризовать всю

генеральную совокупность. Для оценки совокупности изделий по случайной

выборке

применяют

метод,

основанный

на

построении

Гистограммы

Распределения.

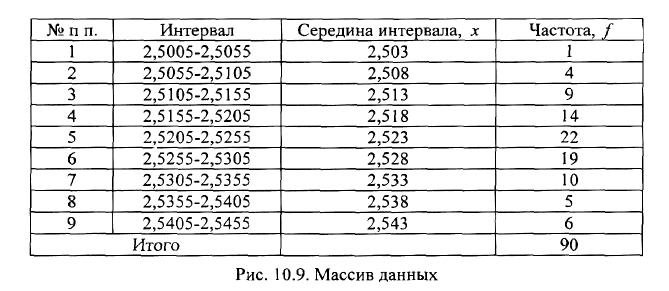
Подготовка данных для построения гистограммы. Допустим, что надо

исследовать вероятность достижения заданной точности диаметра наружной

поверхности оси, обрабатываемой на токарном станке в размер 32,50 ±0,025. Для

этого из большого количества осей взята выборка в количестве 90 штук. Имеется

банк измеренных диаметров осей, при этом максимальный измеренный диаметр

равен 32,5455 мм, а минимальный-32,5005 мм. Построим гистограмму по данным

измерений диаметров осей. Рассмотрим последовательно этапы подготовки

данных для построения. Этап 1- вычислить размах выборки (R). Размах выборки

равен разности наибольшего и наименьшего значения измерений диаметров:

R=0,045 мм. Этап 2 - определить количество и размеры одного интервала размаха

выборки. Для наглядности гистограммы рекомендуется выбирать при ее

построении от 5 до 20 интервалов равной ширины. Для нашего случая можно

принять количество интервалов равным 9 при ширине одного интервала 0,005 мм.

Этап 3 - подготовить бланк таблицы со следующими графами: номер интервала,

границы интервала, среднее значение интервала, количество измерений в каждом

интервале (рис. 10.9). Этап 4 - определить границы интервалов. Нижняя граница

первого интервала равна минимальному значению измерения в выборке, а верхняя

граница равна сумме значения нижней границы и величины интервала. Нижняя

граница второго интервала равна верхней границе первого. И так далее до девятого

интервала, у которого верхняя граница равна максимальному значению

измеренного диаметра. Этап 5 -вычислить значение середины каждого интервала.

Очевидно, что средняя точка каждого интервала имеет среднее значение границ

интервала. Этап 6 - заполнить таблицу на рис. 10.9.

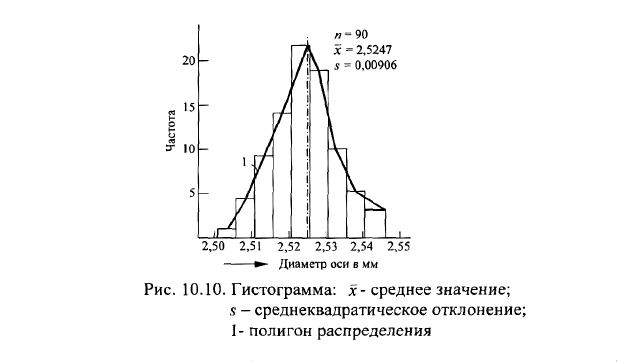
Как строить гистограмму? Этап 1 - взять лист бумаги (лучше в клеточку)

и нанести на него горизонтальную линию, на которой будем откладывать

значения измерений диаметров осей. Масштаб по оси выбирается из соотношения

размера листа и среднего значения размаха выборки. Например, каждые 10 мм

листа соответствуют ширине одного интервала 0,005 мм. Нанести на

горизонтальной оси весь размах с разметкой каждого интервала. Оставить при

этом слева и справа свободные места, равные ширине одного интервала.

Обозначить точками середины каждого интервала. Этап 2 - нанести на бумагу

вертикальную ось. Место пересечения с горизонтальной осью - крайняя левая

точка добавочного (нулевого) интервала. Масштаб по оси выбирается из

соотношения размера листа и максимального количества измерений в одном

интервале. Например, на каждые 25 мм листа-5 измерений. Этап 3 - построить в

каждом интервале прямоугольники, высота которых соответствует количеству

измерений в интервале (рис. 10.10). Построенная столбчатая диаграмма и есть

гистограмма распределения. Нанесем на гистограмму линию, состоящую из

отрезков, соединяющих точки середин интервалов на верхних полках

прямоугольников. Непрерывная линия, соединяющая середины интервалов по

верхним полкам, называетсяполигоном распределения. При увеличении

количества интервалов и уменьшении их ширины полигон распределения

превращается впрактическую кривую распределения. Расстояние между

крайними точками перво-го и последнего интервала называетсяразмахом или

Полем рассеивания.

Сравнение гистограммы с границами допуска. При сравнении и анализе

величин и взаимного положения полей допуска и рассеивания можно выделить 5

типичных вариантов.

Первый вариант. Поле рассеивания значительно меньше поля допуска, ω < Т

(рис.10.11, а). Технологический процесс протекает нормально, требуется только

поддерживать существующее состояние.

Второй вариант. Поле рассеивания равно или немного меньше поля допуска,

ω = Т (рис. 10.11, б). Технологический процесс протекает нормально, но нет запаса

надежности. Можно провести мероприятия по уменьшению поля рассеивания,

если затраты на эти мероприятия будут меньше, чем потери от возможного

брака.

Третий вариант. Поле рассеивания меньше поля допуска, но смещено влево

(или вправо) от границы поля допуска (рис.10.11, в). Процесс ненормальный.

Необходимо добиться смещения середины поля рассеивания к центру поля

допуска.

Четвертый вариант. Поле рассеивания больше поля допуска (ω > Т) и

размещено симметрично относительно центра поля допуска (рис. 10.11, г). Процесс

ненормальный. Необходимо провести мероприятия по уменьшению поля

рассеивания.

Пятый вариант. Поле рассеивания больше поля допуска и смещено

относительно центра допуска (ри с.10.11, д). Процесс ненормальный. Это

худший вариант взаимного положения полей, при котором количество

забракованных изделий возрастает. Необходимо прежде всего добиться

симметричного расположения полей, посчитать затраты от брака и принять (или

не принять) дополнительные мероприятия по уменьшению поля рассеивания.

Для нашего конкретного примера допуск на диаметр составляет 0,05 мм, а

поле рассеивания 0,045 мм. Таким образом, поле рассеивания меньше величины

поля допуска. Одновременно минимальное и максимальное измеренные значения

диаметров меньше соответствующих минимальной и максимальной гра-

ниц поля допуска. Можно сделать заключение, что операция точения обеспечивает

необходимую точность диаметра наружной поверхности оси. Однако разница

между величинами полей невелика, что при малейшей неточности в настройке

технологической системы может привести к появлению брака.