Диаграммы рассеивания

При анализе и регулировании технологических процессов часто возникает

необходимость выявления зависимостей между отдельными показателями

процесса. Например, при обработке резанием очень важно знать зависимость сил

резания от величины подачи или оценить зависимость обрабатываемости

материалов от их механических свойств. Для изучения зависимостей между

двумя переменными на практике применяют так называемыедиаграммы

рассеивания. Эти переменные могут быть как зависимы, так и независимы друг

от друга. Для выявления связи между ними, прежде всего, надо построить

диаграмму рассеивания.

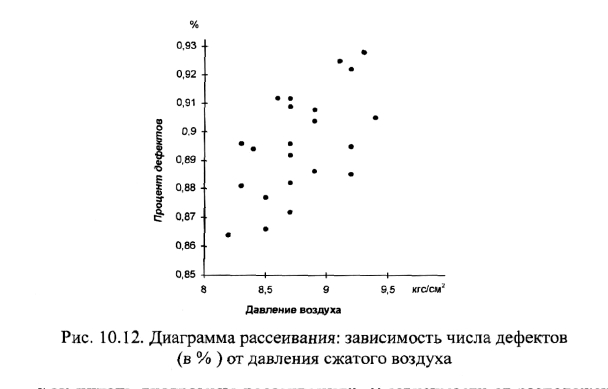
Как построить диаграмму рассеивания? Этап 1 - собрать парные данные

(х, у), между которыми необходимо исследовать зависимость. Рекомендуется не

менее 30 пар данных. Этап 2 - найти максимальное и минимальное значения для х

и у. Выбрать шкалы на горизонтальной и вертикальной оси так,

чтобы обе длины рабочих частей шкал были приблизительно одинаковы. Если

одна переменная - фактор, а другая - характеристика качества, то выбрать для

фактора горизонтальную ось, а для характеристики - вертикальную. Этап 3 —

начертить на листе бумаги график и нанести на него данные измерений. Если

встречаются одинаковые значения пар, то нанести вторую точку рядом с пер-

вой. Этап 4 - нанести на графике обозначения координат (х, у) или названия

переменных, а также численные значения величин (рис. 10.12).

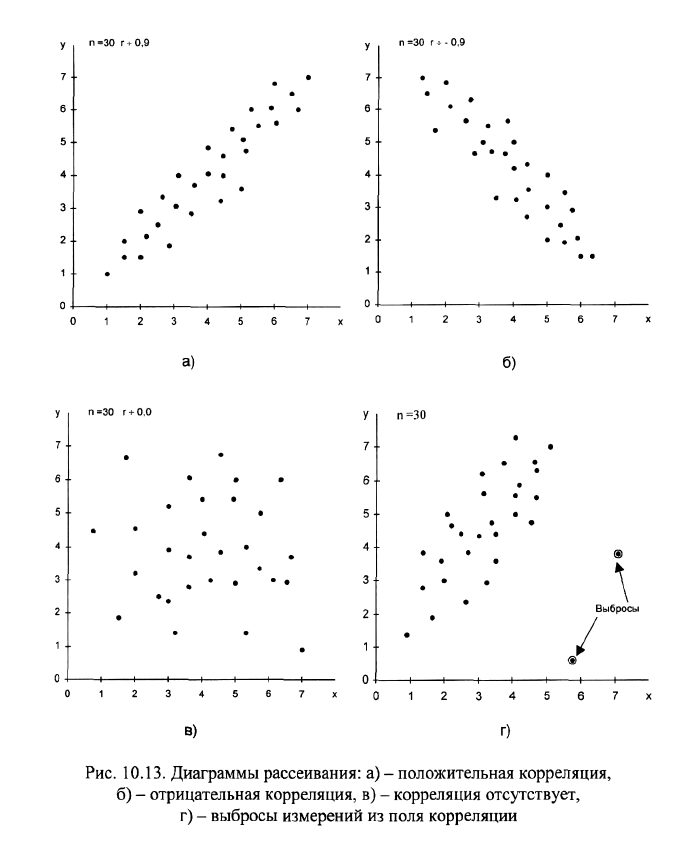
Как читать диаграммы рассеивания? В зависимости от расположения

точек в поле рассеивания можно предварительно проанализировать характер

зависимости между переменными. Если точки выстраиваются на условной на-

клонной линии снизу вверх, то можно сказать, что имеется положительная (рис.

10.13, а) зависимость (корреляция), если точки выстраиваются по линии сверху

вниз, то говорят об отрицательной (рис. 10.13, б) корреляции. Если на глаз не-

возможно определить корреляцию (рис. 10.13, в), то зависимость между двумя

переменными, скорее всего, отсутствует. Возможно наличие на графике точек,

стоящих в стороне от основного массива данных (рис.10.13, г). Это может быть

вызвано как ошибками измерения или описками в записи, так и случайными

выбросами, которые можно не учитывать в анализе корреляции.

Наглядная оценка диаграммы носит, как было сказано, предварительный

характер. Для более точной оценки зависимости проводится математическая

обработка массива парных данных, которая дает численное значениекоэффи-

циента корреляции г. Этот математический метод определения корреляции

между анализируемыми параметрами называетсякорреляционным анализом.

Математическое определение уравнения зависимости между переменными

параметрами

называется

Регрессионным

Анализом.

Рассмотрение

математических методов анализа зависимости не входит в содержание настоящего

пособия. Вместе с этим следует отметить, что коэффициент корреляции

принимает значения в диапазоне -1 < г < 1.

При г, близком к 1(0,8-0,95), имеет место сильная корреляция. При г, близком

к 0 (0,05-0,2), корреляция отсутствует. Можно уверенно считать, что корреляция

существует при коэффициенте корреляции г больше 0,6. Если у исследователя

есть уверенность в наличии корреляции, а диаграмма рассеивания это не

показывает, то целесообразно дополнительно проанализировать собранную

информацию на возможность расслоения данных измерения. Возможно, при

сборе

информации

одна

из

переменных

имеет

дополнительный

стратифицирующий фактор. Например, при определении зависимости силы

резания от величины подачи не учли, что обрабатываемые заготовки были

изготовлены не из одного материала, а из нескольких.

Для оценки эффективности затрат на повышение качества можно так же

использовать математический аппарат корреляционного анализа. Исследуя за-

висимость цены (или рентабельности) от величины издержек, можно по значе-

нию коэффициента корреляции этой зависимости оценить целесообразность

дополнительных расходов на качество.

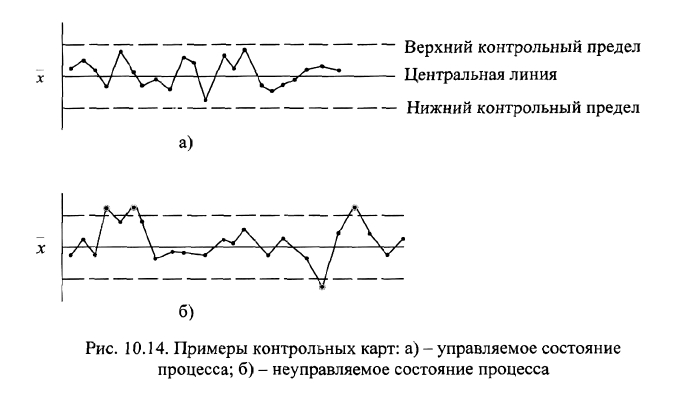
Контрольные карты

Что такое контрольные карты? Впервые контрольные карты были

предложены в 1924 году У.Шухартом (США) с намерением отделить вариации

параметров технологического процесса, которые обусловлены определенными

причинами, от тех, которые вызваны случайными причинами. Контрольная

карта состоит из центральной линии, пары контрольных пределов, по одному

над и под центральной линией, и значений параметров (показателей качества),

нанесенных на карту для представления состояния технологического процесса.

Если все значения параметров оказываются внутри контрольных пределов, не

проявляя каких-то особенностей в расположении, то процесс считается

контролируемым (рис. 10.14, а). Если же, напротив, они попадут за

контрольные пределы или проявят какие-то особенности в расположении, то

процесс считается вышедшим из-под контроля (рис. 10.14, б). Под вариациями

(отклонениями), вызванными определенными причинами, понимаются вариации

в пределах требования стандарта или в пределах обоснованных отклонений.

Например, мы ожидаем от каждой заготовки, выполненной из стали 20, значений

механических

свойств в определенном диапазоне, регламентированном

стандартом или гарантированном в сертификате на материал. Если измеренные

механические свойства оказываются за пределами ожиданий (перепутали марку

стали, брак отливки, погрешности измерений), то мы считаем такое отклонение

случайным. Оно бывает достаточно редко, но от него нельзя избавиться, и оно

приводит к несоответствию требуемого качества изделия. В зависимости от вида

показателя качества и от цели проверки существуют различные типы

контрольных карт.

Типы контрольных карт. Существует два типа контрольных карт: для

непрерывных значений параметров и для дискретных. В свою очередь карты

для непрерывных значений делятся на: (х - И)карты (среднее значение и

размах), х - карты (измеряемые значения). Карты для дискретных значений

делятся на: рп- карты (число дефектных изделий), р- карты (доля дефектов), с-

карты (число дефектов), и- карты (число дефектов на единицу). Рассмотрим

некоторые из них более подробно.

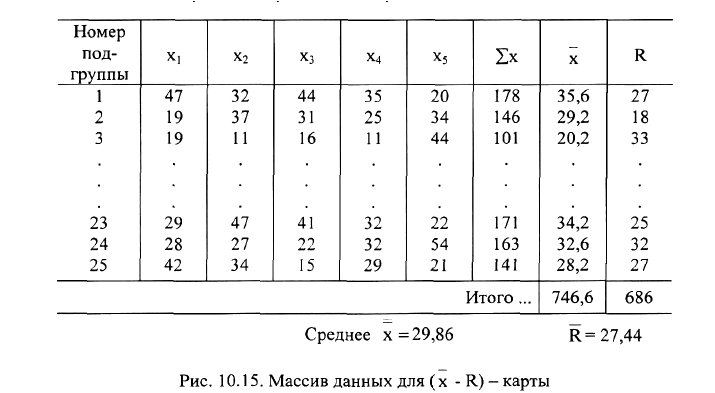
Построение (х -R) карты. Эта карта используется для анализа и управления

процессом, показатели качества которого представляют собой непрерывные

величины (длина, вес, концентрация) и несут наибольшее количество

информации о процессе. Величина x- есть среднее значение для подгруппы

данных, a R - выборочный размах для той же подгруппы. Рассмотрим порядок

построения карты. Этап 1 - собрать данные. Общее количество данных об

исследуемом показателе качества не должно быть меньше 100. Данные

необходимо разделить на 20-25 подгрупп объемом 4-5 каждая. Заполнить

приготовленную таблицу (рис. 10.15). Этап 2 - вычислить в каждой подгруппе

среднее значение параметра х и размах R. Записать в таблицу. Этап 3 -

вычислить среднее значение всей группы данных х как среднее арифметическое

средних значений х подгрупп. Этап 4 - вычислить среднее значение размаха R

группы как среднее арифметическое размахов R подгрупп. Записать в таблицу.

Этап 5 - вычислить значение контрольных линий по нижеприведенным

формулам, отдельно для х - карты и R- карты:

x - карта. Центральная линия: CL = x .

Верхний контрольный предел: UCL = x + α R .

Нижний контрольный предел: LCL = x - α R ,

карта. Центральная линия: CL = R .

Верхний контрольный предел: UCL = β1 R .

Нижний контрольный предел: LCL = β2 R .

Нижний предел не рассчитывается, когда объем подгруппы меньше 6. Для

нашего примера (объем подгруппы равен 5) имеем следующие коэффициенты

для расчета контрольных линий α = 0,577; β1= 2,115; β2= 2,326.

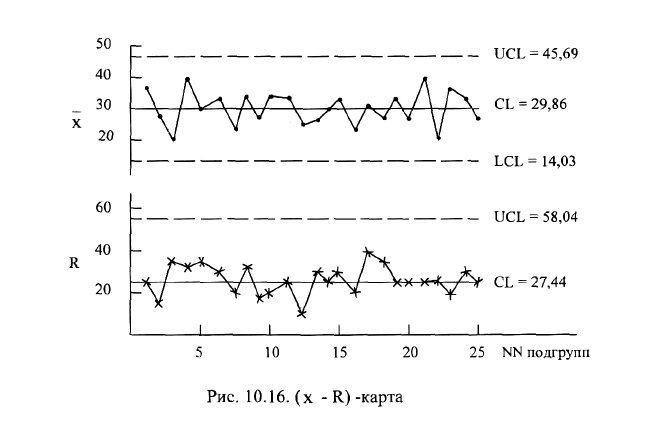
Этап 6 - построить контрольные карты. Приготовить лист бумаги (лучше в

клеточку), затем нанести отдельно для x и R горизонтальные оси с номерами

подгрупп. Центральную линию нанесите сплошной линией, а контрольные пре-

делы - пунктирными линиями. Нанести вертикальные оси, разметить на них

величины контрольных пределов. Нанести на графики точки средних значений x

и значений размахов R каждой подгруппы (рис.10.16).Чтобы легче различать x и

R, выбирают для x знак · (точка), для R - х (крестик), а для тех значени й

параметров, которые выходят за пределы - кружочки.

Этап 7- записать необходимую информацию. Обычно в верхнем левом углу x -

карты пишется объём подгруппы (n), а также другие необходимые сведения,

имеющие отношение к изучаемому процессу, такие как название процесса и

продукта, период времени, метод измерения, условия работы, смена, участок и т.д.

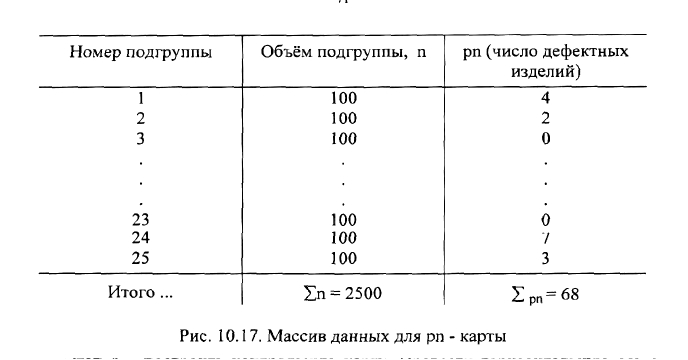
Построение рп- карты. Эта карта применяется в тех случаях, когда пока-

затель качества представлен целым числом дефектных изделий. Рассмотрим

порядок построения карты. Этап 1 - взять выборку исследуемых изделий такого

объема, чтобы в среднем в каждую подгруппу попадало от одного до шести

негодных изделий, и собрать 20-25 таких подгрупп. Для наглядности изложения

приведем банк данных (рис. 10.17). Этап 2 - вычислить среднюю долю дефектов

в выборке р, деля общее число дефектов в каждой подгруппе Zpn на общее

число изделий в подгруппах kn.

p =

¦ pn

kn

В нашем примере р = 0,0272.

Этап 3 - вычислить значения контрольных линий.

Центральная линия: CL = рn.

Верхний контрольный предел: UCL = рn + 3 pn(1 − p)

Нижний контрольный предел: LCL = рn - 3 pn(1 − p) .

Нижний предел не рассматривается, если его значение - отрицательное

число. В нашем примере CL = 2,72; UCL = 7,60; LCL = отрицательное число.

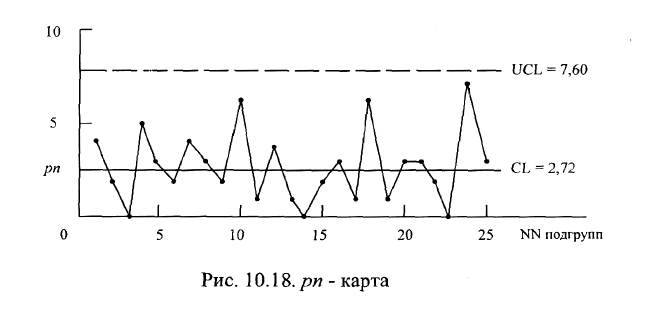
Этап 4 - построить контрольную карту. Провести горизонтальную ось с

номерами подгрупп k и вертикальную ось с числами дефектов рп. Сплошной

линией начертить центральную линию CL, а пунктирными линиями - верхний и

нижний пределы UCL и LCL (рис. 10.18).

Как читать контрольные карты? В зависимости от расположения точек

значений параметров на графике можно судить о состоянии технологического

процесса. Отметим, что контролируемое состояние процесса - это такое

состояние, когда процесс стабилен, а его среднее и разброс не меняются.

Рассмотрим различные состояния процесса.

Выход за контрольные пределы. Такое состояние, при котором точки

значений параметров лежат вне контрольных пределов.

Серии. Состояние процесса, при котором точки неизменно оказываются

по одну сторону от центральной линии. Число таких точек называетсядлин-

ной серией. Серия длиной всемь точек рассматривается как ненормальная. Со-

стоянием является ненормальным и тогда, когда число последовательных точек

меньше семи, но не менее 10 из 11(или 12 из 14, или 16 из 20) точек оказыва-

ются по одну сторону от центральной линии.

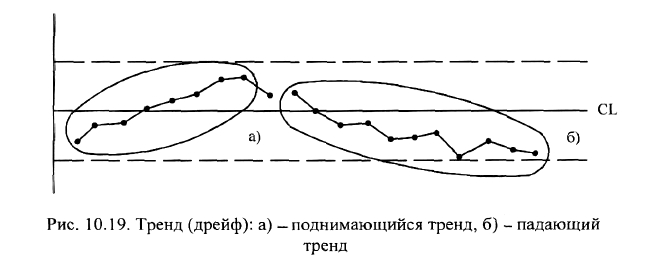
Тренд (дрейф). Тренд- это проявление такого (ненормального) состояния

процесса, когда точки (не менее семи подряд) образуют непрерывно повы-

шающую или понижающую кривую (рис. 10.19).

Приближение к контрольным пределам. Провести ниже от верхнего

контрольного предела и выше от нижнего 2- сигмовые контрольные пределы

(не забыть, что контрольные пределы - 3- сигмовые). Если достаточно часто две

из трех последовательных точек оказываются в зонах между 2- и 3- сигмо-выми

пределами, то рассматривать такой процесс ненормальным.

Приближение к центральной линии. Когда большинство точек концен-

трируется в пределах 1,5- сигмовой зоне выше и ниже центральной линии, не-

обходимо рассматривать такой процесс ненормальным, что обусловлено не-

подходящим способом разбиения данных измерений на подгруппы. Приближение

к центральной линии вовсе не означает, что достигнуто контролируемое

состояние, напротив, это значит, что в подгруппах смешиваются данные из

различных распределений, что делает размах контрольных пределов слишком

широким. Надо менять способ разделения на подгруппы.

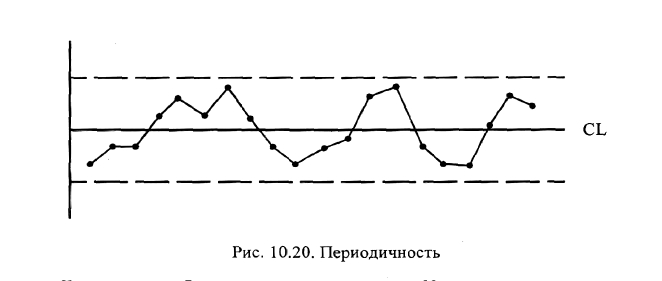
Периодичность. Состояние, когда точки располагаются по кривой, напо-

минающей синусоиду (рис. 10.20) с примерно одинаковыми интервалами вре-

мени, называется периодичностью. Такой процесс считается ненормальным.

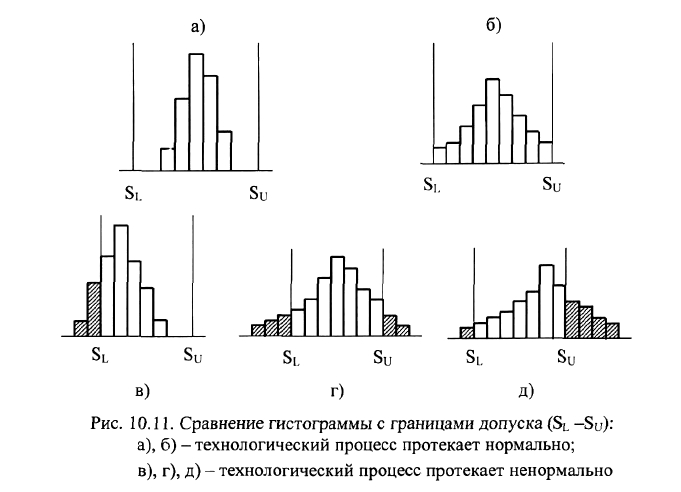
Сравнение разброса с границами допуска. Управление процессом только

на основании анализа одних контрольных карт может привести к неправильным

выводам о качестве его состояния. Для полной картины нужно сравнивать данные

о процессе с границами поля допуска на контролируемый параметр (показатель

качества). Если гистограмма распределения, построенная на основе значений

контролируемого параметра, укладывается в пределы допуска вместе с крайними

значениями, это свидетельствует, что процесс удовлетворяет установленным

стандартам или требованиям. С другой стороны, если гистограмма выходит за

верхнюю и нижнюю границы допуска, то это означает, что процесс

неудовлетворителен. Но, даже если процесс находится в контролируемом

состоянии, все равно может производиться некондиционная продукция. Почему?

Контрольные пределы устанавливаются для того, чтобы можно было

определить, находится ли процесс в контролируемом состоянии или нет, границы

поля допуска необходимы для того, чтобы можно было узнать, дефектно ли

каждое отдельное изделие или нет. Границы поля рассеивания (контрольные

пределы) определяются вариацией параметра от случайных причин. То есть не

зависят от желания конструктора, в то время как границы поля допуска

выбираются в за-висимости от требований потребителя (через конструктора).

Разберем на при-мере наиболее часто встречающиеся варианты течения процесса

(рис.10.21):

а - процесс в неконтролируемом состоянии, имеет место брак,

б - процесс в контролируемом состоянии, но, тем не менее, брак есть,

в - процесс в неконтролируемом состоянии, но брака нет,

г- процесс в контролируемом состоянии, брака нет.

Варианты а) и г) не требуют комментариев, но варианты б) и в) нуждаются в

объяснении. В варианте б) все точки лежат в поле рассеивания (между

контрольными пределами), но величина их размаха больше поля допуска. Идет

брак. В варианте в) поле рассеивания укладывается в поле допуска, но к браку

могут привести случайные выбросы значений параметров. Необходимо

снижать величины факторов рассеивания, то есть улучшать качество процесса.