Задача доказательства нормальности распределения значений исследуемого признака

Нормальный характер распределения является необходимым условием для применения параметрических критериев. В частности t-критерия Стьюдента и коэффициента корреляции Пирсона (r_xy).

Наиболее простым способом доказательства является расчет коэффициентов ассиметрии (А) и эксцесса (Е).

Расчет производится по формулам:

Асимметрия

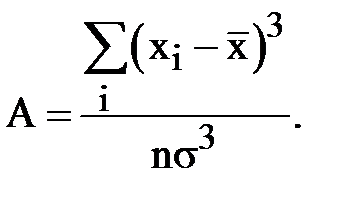
Если А< 0, то эмпирическое распределение несимметрично и сдвинуто вправо. При 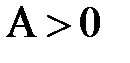распределение имеет сдвиг влево. При 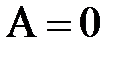распределение симметрично.

Эксцесс.Показатель, характеризующий выпуклость или вогнутость эмпирических распределений:

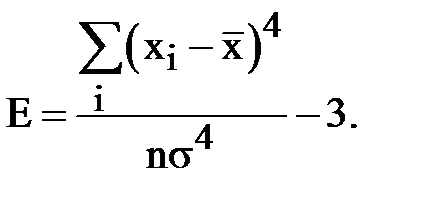
Если 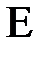больше или равно нулю, распределение выпукло, в других случаях – вогнуто. В идеальном нормальном распределении значения эксцесса и асимметрии равны нулю. Однако, в зависимости от объема выборки, можно считать эти значения незначимыми. Интервал незначимости определеятся от нуля до критического значения эксцесса и асимметрии, которые расчитываются по формулам:

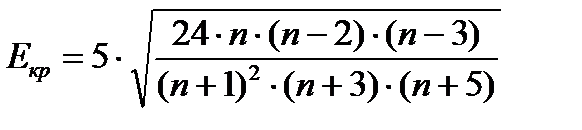
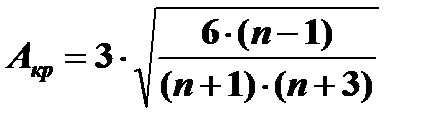
где n – объем выборки испытуемых.

Распределение значений исследуемого признака можно считать нормальным только в том случае, если одновременно и значения эксцесса, и значения ассимметрии меньше критических (без учета знаков). Эмпирические значения эксцесса и асимметрии «вручную» расчитываются очень трудоемко, поэтому рекомендуется воспользоваться программой Excel (Приложение 3).