Статистическая совокупность. Статистические величины
Объектом любого статистического исследования является статистическая совокупность — группа или множество относительно однородных элементов, т. е. единиц, взятых вместе в конкретных границах времени и пространства и обладающих признаками сходства и различия.
Различают два вида статистической совокупности: генеральную, состоящую из всех единиц наблюдения, которые могут быть к ней отнесены в зависимости от цели исследования, и выборочную – часть генеральной совокупности, отобранную специальным выборочным методом. Каждую статистическую совокупность можно рассматривать как генеральную и как выборочную.
Целью изучения любой статистической совокупности является выявление общих свойств, общих закономерностей различных явлений, так как эти свойства не могут быть обнаружены при анализе единичных явлений.
Признаки сходства служат основанием для объединения единиц в совокупность, признаки различия, называемые учетными признаками, являются предметом их особого анализа. По своему характеру учетные признаки могут быть качественными (например, пол, профессия). Они могут быть также количественными, выраженными числом (например, возраст).
Одним из типов распределения признака в статистической совокупности является вариационный ряд - ряд числовых значений какого-то определенного признака, отличающихся друг от друга по своей величине и расположенных в ранговом порядке.
Характеристиками вариационного ряда являются:
w числовое значение изучаемого признака (Х);
w частота, с которой встречается каждый признак (р);
w общее число наблюдений (N).
Вариационный ряд может быть простым, где значение каждого признака обозначается отдельно, или сгруппированным, где значение признака объединяются в группы с указанием частоты встречаемости признака, входящего в данную группу.
Простой вариационный ряд составляется обычно при малом числе наблюдений (N ≤ 30), а сгруппированный – при большом числе наблюдений (N >30).
Для оценки изучаемых явлений, составляющих статистическую совокупность, используют следующие статистические средние величины:
мода (Мо) — величина признака, чаще других встречающегося в совокупности;
медиана (Ме) — величина, которая делит распределение пополам: половина значений больше медианы, половина меньше.
среднее по совокупности(М) – величина, равная отношению суммы всех значений признака к их общему числу членов совокупности:
 , (13.1)
, (13.1)
где: М – среднее по совокупности;
X i – значение признака одного члена совокупности;
N – число членов совокупности.
Разнообразие признака в вариационном ряду. Имеются следующие критерии разнообразия признака:
1. Характеризующие границы совокупности.
2. Характеризующие внутреннюю структуру совокупности - стандартное отклонение (σ)– это показатель разброса значений относительно среднего.
Для того чтобы охарактеризовать разброс значений относительно среднего введем показатель разброса, который носит название дисперсиии обозначается σ2 . Ясно, что для характеристики разброса признака все равно в какую сторону отклоняется значение – в большую или в меньшую. Иными словами, отрицательные и положительные отклонения должны вносить равный вклад в характеристику разброса. Воспользуемся тем, что квадраты двух равных по абсолютной величине чисел равны между собой, и вычислим средний квадрат отклонения от среднего, т.е. σ2. Чем больше разброс значений, тем больше дисперсия.
 (13.2)
(13.2)
Дисперсия измеряется в единицах, равных квадрату единицы измерения соответствующей величины. Поэтому чаще используется квадратный корень из дисперсии - стандартное отклонение:
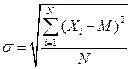 (13.3)
(13.3)
3. Коэффициент вариации (Сх), который характеризует разнообразие признака в вариационном ряду и вычисляется по формуле:
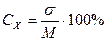 (13.4)
(13.4)
Если Сх < 10% – слабое разнообразие признака,
Сх = 10 - 20 % – среднее разнообразие признака,
Сх > 20 % – сильное разнообразие признака.
| ? | Пример выполнения работы |
Цель работы:Определение среднегоуровня изучаемого признака - средней величины, использующихся для анализа медицинских данных, заключенных в вариационном ряду.
Необходимо:
1. В Excel набрать заданный вариационный ряд статистических данных.
2. Расположить значения признака в ранговом порядке (отсортировать по возрастанию).
3. Вычислить следующие статистические величины с помощью встроенных статистических функций Microsoft Excel: среднее по совокупности, стандартное отклонение, моду, медиану.
4. Коэффициент вариации вычислить по формуле (4).
5. По полученному значению коэффициента вариации определить характер разнообразия признака.
Данные: В результате измерения длины тела у 32 мальчиков при рождении были получены следующие данные (в см): 49, 52, 54, 49, 52, 54, 50, 49, 53, 52, 54, 50, 50, 54, 49, 51, 51, 53, 51, 52, 53, 48, 48, 55, 56, 55, 49, 53, 52, 52, 50, 51.
Введем исходные данные в таблицу Excel и отсортируем их в ранговом порядке
 |  |
Используя встроенные функции Excel, вычислим значения статистических величин, характеризующих статистическую совокупность и по полученному значению коэффициента вариации определим характер разнообразия признака.
 |  |
| è | Порядок выполнения работы |
1. Изучение теоретического материала.
2. Выполнение вариантов заданий с помощью рассмотренных инструментов, средств, приемов и технологий
3. Составление отчета о проделанной работе. Отчет должен содержать следующие разделы:
наименование работы;
цель работы;
пошаговое последовательное описание процесса выполнения варианта задания по видам выполняемых действий.
4. Результат выполнения варианта задания должен быть сохранен под именем ФИО_Работа№_Вариант№ (например, «ИвановНН_Работа1 _Вариант1.xls») на жесткий диск в папку «Мои документы\ИТ в медицине» и на дискету – в двух копиях (две копии одной и той же информации в разных папках на дискете).
5. Представление результатов выполнения работы (отчета и файлов на дискете) для проверки преподавателю.
6. Защита выполненной работы: ответ на контрольные вопросы к теоретическому материалу занятия и ответ на замечания преподавателя по выполненной работе.
7. Оценка преподавателем выполненной работы.
| s | Контрольные вопросы |
1. Перечислите этапы медико-статистического исследования.
2. Дайте краткую характеристику первого этапа исследования.
3. Какие задачи решаются на втором этапе исследования.
4. Опишите общие правила уточнения и формулирования признаков на третьем этапе исследования.
5. Охарактеризуйте задачи четвертого этапа исследования.
6. Дайте определение статистической совокупности. Какие бывают виды статистической совокупности.
7. Что является целью изучения статистической совокупности.
8. Дайте определение вариационного ряда.
9. Перечислите характеристики вариационного ряда.
10. Что представляют собой простой и сгруппированный вариационный ряд?
11. Какие статистические величины используются для оценки изучаемых явлений?
12. Каковы критерии разнообразия признака?
13. Что такое дисперсия?
14. Дать определение стандартного отклонения.
15. Что характеризует коэффициент вариации?
| Ä | Варианты заданий |
| Вариант 1 | 15 - 20 мин. |
Содержание жира в материнском молоке у 7 женщин (в граммах): 3,8; 4,2; 5,0; 4,8; 3,6; 4,2; 4,5. Найдите среднее, стандартное отклонение, моду, медиану и определите коэффициент вариации.
| Вариант 2 | 15 - 20 мин. |
Результаты измерения длины тела у 47 девочек (в см): 48, 51, 53, 49, 51, 53, 51, 48, 52, 51, 53, 49, 50, 53, 48, 52, 50, 52, 50, 52, 50, 51, 52, 53, 47, 52, 48, 48, 52, 50, 46, 46, 54, 55, 56, 48, 52, 52, 51, 53, 53, 48, 50, 54, 48, 50, 50. Найдите среднее стандартное отклонение, моду, медиану и определите коэффициент вариации.
| Вариант 3 | 15 - 20 мин. |
Число обращений за первые сутки в течение 12 месяцев календарного года в скорую медицинскую помощь города составляет: 165, 161, 167, 165, 164, 163, 142, 143, 137, 156, 151, 147. Найдите среднее, стандартное отклонение, моду, медиану и определите коэффициент вариации.
| Вариант 4 | 15 - 20 мин. |
На 15 лекциях по социальной гигиене и организации здравоохранения в весеннем семестре на одном из потоков 5-го курса присутствовало студентов: 174, 183, 190, 168, 175, 158, 172, 180, 174, 170, 171, 155, 169, 174, 168. Найдите среднее, стандартное отклонение, моду, медиану и определите коэффициент вариации.
| Занятие №14 | Графический анализ данных. Изучение распределения случайных величин, подчиняющихся нормальному закону распределения Гаусса |
| Цель работы |
Развить и закрепить навыки изучения нормального распределения, подчиняющегося закону Гаусса, и построения графиков распределения.
| & | Теоретический материал |
Цели, которые преследуются при построении графиков, следующие:
1. Представить наглядно сущность и характер изучаемых явлений.
2. Популяризовать результаты статистических исследований.
3. Оказать помощь при анализе изучаемых явлений.
Графики позволяют наглядно представить статистические показатели, полученные при анализе результатов проведенного исследования. Они облегчают сравнение показателей, дают представление о характере связи между явлениями и указывают на тенденции их изменения во времени. Графическое изображение статистических данных в сравнении с табличным позволяет быстро и легко заметить существующие закономерности- Эти последние ярче выражены и подчеркнуты, усваиваются легче и быстрее запоминаются. Вместе с этим связь между статистическими показателями заметна полнее и нагляднее, а скрытые закономерности становятся явственнее. Это создает условия для углубленного исследования и способствует аналитическому мышлению.
В научно-исследовательской работе необходимо хорошо владеть методами графического анализа.
При составлении графиков исследователь должен придерживаться некоторых основных правил. Он должен предварительно внимательно изучить данные, которые следует представить графически. Во-вторых, исследователь должен хорошо знать статистические методы анализа, с помощью которых получены данные. Комбинируя эти два требования, он сможет выбрать наиболее подходящее для данного случая графическое изображение. При таком выборе исследователь принимает во внимание также следующее:
1. Характер данных. Нужно отметить, что некоторые данные не поддаются графическому изображению. Для других подходят графики только определенного типа. Так, например, если ставится задача изобразить структуру данного явления, то наиболее подходящими будут секторные диаграммы; для изображения динамики явлений во времени наиболее подходят линейные диаграммы; если изображается сезонность, то наиболее подходят линейно-круговые диаграммы и т. д.
2. Назначение графиков. Они могут быть использованы для различных целей (для репродукций в книгах, для лекций, выставок, диапозитивов, кино или телевидения). В зависимости от того, для чего предназначен график, подбирают его величину, характер линий, используемые штрихи и краски, шрифт, величину букв и т. д.
3. Цель графиков. Очень часто цель графических изображений – наглядно представить результаты проведенного исследования. В других случаях – подчеркнуть известные закономерности, иллюстрировать новые открытые факты, выдвинуть и обосновать новые гипотезы.
4. Аудитория, для которой предназначены графические изображения. Нужно учитывать уровень знаний аудитории, ее практические и научные интересы и пр. Так, например, графики, предназначенные для широкой аудитории, не должны быть сложными в техническом отношении. Для такой аудитории можно использовать фигурные диаграммы. Графики же, предназначенные для высококвалифицированных специалистов, могут быть технически сложнее.
Графики можно условно разделить на следующие группы.
1. Линейные диаграммы.
2. Плоскостные диаграммы.
3. Фигурные диаграммы.
4. Объемные диаграммы.
5. Картограммы.
6. Картодиаграммы.
Если значения интересующего нас признака у большинства объектов близки к их среднему и с равной вероятностью отклоняются от него в большую или в меньшую сторону, то есть на изменение признака оказывают незначительное влияние внешние факторы, то такое распределение учетного признака называется нормальным (гауссовым), описывается формулой:
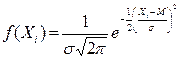 (14.1)
(14.1)
и полностью определяется следующими статистическими параметрами:
w среднее значение;
w стандартное отклонение 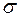 (см. занятие 13, формула 13.3).
(см. занятие 13, формула 13.3).
Если значения признака распределены несимметрично относительно среднего, то распределение не является нормальным и совокупность лучше описать с помощью:
w медианы МЕ;
w процентилей.
Займемся исследованием количественного признака, например роста.
Проведем исследование на планетах Марс и Венера. Отметим, что все жители одной планеты образуют генеральную статистическую совокупность. Для исследования отберем 200 марсиан и 150 венерианцев, где каждая из двух групп инопланетян является выборочной статистической совокупностью, а каждый инопланетянин – единицей наблюдения. Измерим рост каждой единицы наблюдения и запишем в простой вариационный ряд.
В результате получили два простых вариационных ряда: рост марсиан и рост венерианцев. В Microsoft Excel следует набрать получившиеся вариационные ряды. Для наглядности картины распределения роста преобразуем простые вариационные ряды в сгруппированные и расположим значение исследуемого признака (роста) по возрастанию (в ранговом порядке). Сгруппированные ряды представлены ниже::
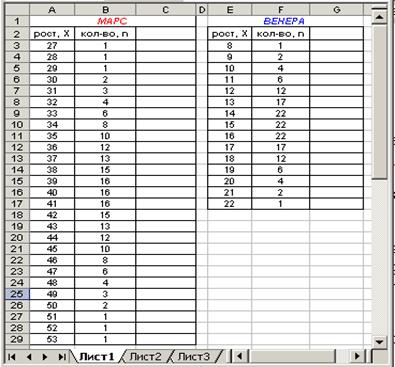
Используя встроенные функции Excel (см. Раздел 2, Занятие 2), вычислим среднее по совокупности и стандартное отклонение, как показано на следующем рисунке:

Получим средний рост марсиан 40 см, а венерианцев – 15 см. Стандартное отклонение роста у марсиан составляет 4,8 см, у венерианцев – 2,6 см.
Для наглядности картины распределения роста у марсиан и венерианцев воспользуемся графическим изображением в виде графика. С помощью мастера диаграмм построим графики распределения роста у марсиан и венерианцев.

На графике «Распределение роста марсиан» мы видим, что Марсиан среднего роста больше всего, высокорослых столько же, сколько коротышек (распределение симметрично). А на графике «Распределение роста венерианцев» – венерианцы ниже марсиан, разброс значений меньше. Однако по форме распределения венерианцы и марсиане схожи друг с другом.
Составим таблицу (см. ниже), которая сжато представляет то, что мы узнали о марсианах и венерианцах. Из нее можно узнать об объеме совокупности, о среднем росте, и о том, на сколько велик разброс относительно среднего.
Дата добавления: 2016-03-05; просмотров: 2383;
