Наибольшее и наименьшее значения функции в замкнутой области

Пусть функция 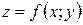определена и непрерывна в ограниченной замкнутой области 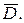Тогда она достигает в некоторых точках 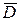своего наибольшего 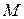и наименьшего 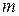значений (т.н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области 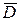, или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значений дифференцируемой в области 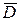функции 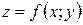состоит в следующем:

1. Найти все критические точки функции, вычислить значение функции в них.

2. Найти наибольшее и наименьшее значение функции на границах области.

3. Сравнить все найденные значения функции и выбрать из них наименьшее и наибольшее.

Пример.

Найти наибольшее и наименьшее значения функции 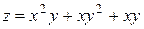в замкнутой области, ограниченной линиями: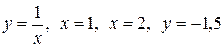

Решение.

1. Находим все критические точки: 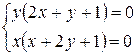решением системы являются точки 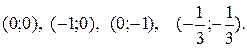ни одна из точек не принадлежит области

2. 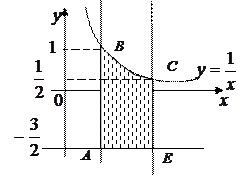Исследуем функцию 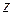на границе области, состоящей из участков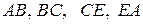

На участке 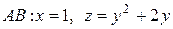, где ,

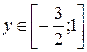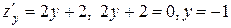. Значения функции ,

.

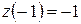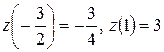На участк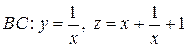е , где 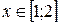. Значения функции .

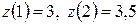На участке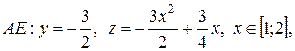

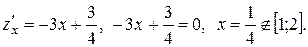
Значения функции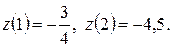

3. Сравнивая полученные результаты, имеем:

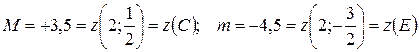
Правило:

1) 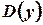Найти частные производные первого порядка и критические точки

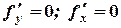
2) Найти частные производные второго порядка и вычислить их значения в критической точке .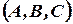

3) Используя достаточное условие (Т.2.2) определить знак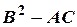и и 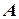и сделать вывод о существовании экстремума.