Необходимые и достаточные условия экстремума

Экстремум функции двух переменных

Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной.

Пусть функция 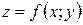определена в некоторой области 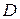, точка .

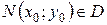Точка 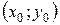называется точкой максимума функции 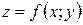, если существует такая 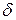- окрестность точки 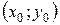, что для каждой точки 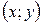, отличной от 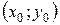, из этой окрестности выполняется неравенство .

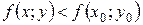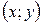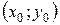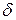Аналогично определяется точка минимума функции: для всех точек , отличных от , из - окрестности точки 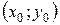выполняется неравенство: 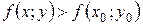. На рис. 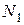- точка максимума, а 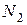- точка минимума функции .

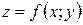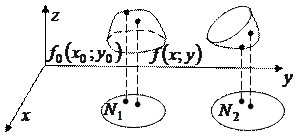Необходимые и достаточные условия экстремума

Теорема(необходимые условия экстремума).

Если в точке 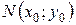дифференцируемая функция 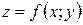имеет экстремум, то ее частные производные в этой точке равны нулю: .

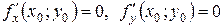Точка, в которой частные производные первого порядка функции 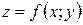равны нулю, т.е. 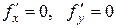, называется стационарной точкойфункции .

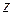Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.

В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума.

Теорема(достаточное условие экстремума).

Пусть в стационарной точке 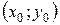и некоторой ее окрестности функции 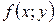имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке 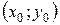значения 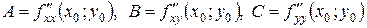. Обозначим .

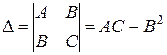Тогда:

1. если 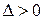, то функция 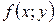в точке 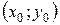имеет экстремум: максимум, если 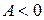; минимум, если ;

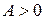2. если 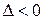, то функция 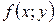в точке 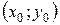экстремума не имеет;

В случае 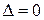экстремум в точке 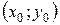может быть, может не быть. Необходимы дополнительные исследования.

Пример.

Найти экстремум функции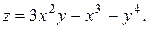

Решение.

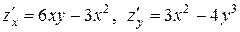. Точки, в которых частные производные не существуют, отсутствуют.

Найдем стационарные точки, решая систему уравнений:

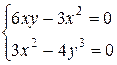
Отсюда получаем точк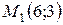и и .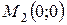

Находим частные производные второго порядка данной функции: .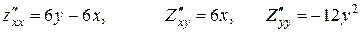

В точке 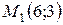имеем: 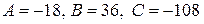, отсюда 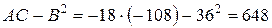, т.е. .

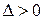Т. к. 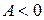, то в точке 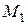функция имеет локальный максимум:

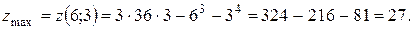
В точке 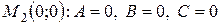и, значит, 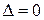. Проведем дополнительное исследование. Значит, в окрестности точки 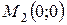функция 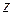принимает как отрицательные, так и положительные значения. Следовательно, в точке 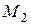функция экстремума не имеет.