Виды средств измерений

Меры воспроизводят физическую величину заданного значения. Они бывают однозначные (например, резистор с сопротивлением 10 Ом) и многозначные (линейка, магазин сопротивлений, магазин емкостей).

Измерительные преобразователи преобразуют сигналы измерительной информации в форму, более удобную для дальнейшего использования.

Примеры:

1) Термопара преобразует температуру в термо-э.д.с.;

2) Измерительный усилитель преобразует меньшее напряжение в большее;

3) Измерительный трансформатор тока преобразует больший переменный ток в меньший.

Измерительные приборы преобразуют сигналы измерительной информации в форму, доступную для восприятия человеком.

Остановимся подробнее на измерительных приборах.

Виды измерительных приборов.

а) По измеряемой величине:

– измерители напряжения U – вольтметры V;

милливольтметры mV;

микровольтметры μV;

киловольтметры kV;

– измерители тока I – амперметры А;

• • •

• • •

•

•

•

б) По форме представления результата:

– аналоговые (шкала и указатель);

– цифровые.

в) По выполняемым функциям:

– показывающие;

– регистрирующие;

– показывающие и регистрирующие.

г) По элементной базе:

· электромеханические; вот символы измерительных механизмов:

· электронные:

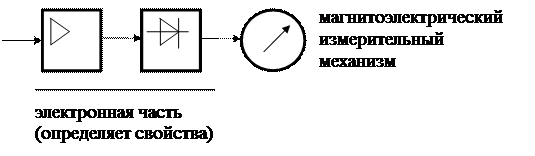
д) По условиям применения:

Меры, измерительные преобразователи и измерительные приборы – это элементарные средства измерения. С добавлением средств вычислений образуются более сложные: измерительно-вычислительные системы и комплексы.

1.3.3. Точность

Количественная характеристика точности – погрешность. Чем меньше погрешность, тем выше точность.

Прежде всего, существуют два понятия:

· погрешность измерения;

· погрешность измерительного прибора.

Это не одно и то же. Можно взять дорогой, очень точный прибор, но получить при неграмотном использовании очень плохой результат. Попробуйте сами привести пример такой ситуации.

Существует три формы выражения погрешностей:

· абсолютная Δ;

· относительная δ:

· приведённая γ.

Погрешность измерения может быть выражена в форме Δ или δ, а погрешность измерительного прибора – в любой из трёх форм.

Абсолютная погрешность измерительного прибора:

Δ = Х – Х_ист ≈ Х – Х_д, (6)

где Х – показание прибора; Х_ист – истинное значение измеряемой величины;

Х_д – её действительное значение.

Относительная погрешность измерительного прибора:

δ = 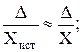δ (%) = 100 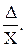(7)

Приведённая погрешность измерительного прибора:

γ = 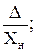γ (%) = 100· 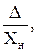(8)

где Х_н – нормирующее значение измеряемой величины.

Что значит «нормирующее значение? Покажу на примерах:

1) У вольтметра с диапазоном измерения от 0 до 15 В нормирующее значение

Х_н = U_н = 15 В.

2) У миллиамперметра с двусторонней шкалой – 5 мА ÷ 0 ÷ 5 мА нормирующее значение

Х_н = I_н = 5 мА (или 10 мА).

3) Частотомер с узким диапазоном измерения 49 Гц ÷ 50 Гц ÷ 51 Гц нормирующее значение

Х_н = f_н = 50 Гц.

Связь относительной погрешности с приведённой:

δ = γ· 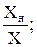δ = γ при Х = Х_н ; δ > γ при Х < Х_н !

Основная погрешность и дополнительные погрешности.

Погрешность Δ зависит от влияющих величин ξ:

Δ = f(ξ₁; ξ₂;… ξ_n).

Влияющие величины – это:

а) внешние факторы – температура, напряжение питания (если оно есть у прибора) и др.;

б) неинформативные параметры входного сигнала.

Пример: u(t) = U_msinωt = 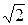Usin2πft

– вольтметром измеряют среднее квадратическое значение U синусоидального напряжения u(t); в этом случае частота f этого напряжения – неинформативный параметр входного сигнала, т.е. такой параметр, который не несёт полезной информации о значении U, но влияет на результат измерения U;

– частотомером измеряют частоту f синусоидального напряжения u(t); в этом случае U – неинформативный параметр входного сигнала.

Нормальные условия применения прибора – это такие условия, когда все влияющие величины ξ_i либо имеют нормальные значения

ξ_i = ξ_i,норм,

либо находятся в пределах нормальных областей значений

ξ_{i,норм,min} ≤ ξ_i ≤ ξ_{i,норм,max}.

ОСНОВНАЯ погрешность Δ_о –это погрешность в нормальных условиях.

Рабочие условия применения прибора – это такие условия, когда влияющие величины ξ_i находятся в пределах рабочих областей значений

ξ_i,раб,min ≤ ξ_i ≤ ξ_i,раб,max.

ДОПОЛНИТЕЛЬНАЯ погрешность Δ_д – это изменение погрешности, вызванное отклонением одной из влияющих величин ξ_i от её нормального значения ξ_i,норм или выходом за пределы нормальной области значений ξ_{i,норм,min} ÷ ξ_{i,норм,max}.

Систематическая и случайная погрешности.

СистематическаяпогрешностьΔ_состаётся постоянной или закономерно изменяется в зависимости от времени (или другого аргумента).

Случайная погрешность изменяется случайным образом.

Пусть Х = const. Производятся повторные измерения Х. Если Х₁; Х₂;…Х_n отличаются друг от друга – значит, проявляет себя случайная погрешность. Что при этом принять за результат измерения? Ответ известен: среднее значение:

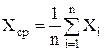. (9)

В вероятностном смысле Х_ср ближе к истинному значению Х_ист, чем любое Х_i. Это объясняется тем, что одни Х_i отличаются от Х_ср в одну сторону, другие – в другую. Чем больше n, тем меньше влияние случайной погрешности, но тем дольше процесс измерения.

Такое измерение с повторами и усреднением называют измерением с многократными наблюдениями: Х_i – это наблюдения, а Х_ср – результат измерения.

Таким образом, простой приём – многократные наблюдения – позволяет обнаружить присутствие случайной погрешности, а их усреднение – снизить её влияние.

Заметим, что этот приём не обнаруживает систематическую погрешность и не снижает её.

Для нахождения Δ_с нужен более точный прибор, показание которого можно считать действительным значением Х_д, и тогда

Δ_с = Х – Х_д (10)

или

Δ_с = Х_ср – Х_д, (11)

если выявлено присутствие случайной погрешности и произведены многократные наблюдения.

Если Δ_с найдена, её можно исключить, введя поправку:

η = – Δ_с. (12)

Тогда Х + η – это будет исправленный результат измерения.

Получается, что если погрешность найдена – это уже не погрешность. Погрешность остаётся погрешностью лишь до тех пор, пока в ней есть неопределённость, случайность. После внесения поправки остаются не исключённые остатки Δ_с, но они уже случайны.

Итак, погрешность – в принципе случайная величина.

Случайные величины можно изучать, у них есть определённые законы. Этим занимается одна из отраслей математики – теория вероятностей. Мы будем её использовать.

Мы рассмотрели случай, когда с помощью более точного прибора находят Δ_с и вводят поправку η. Может возникнуть вопрос: если у нас есть этот более точный прибор, почему бы им и не измерять? Дело в том, что поправка вносится в результаты многих измерений, а определяется редко. Для её нахождения используются эталонные средства измерения. Они служат не для измерений, а для поверки и аттестации рабочих средств измерения. Если бы эталонные средства использовались для измерений, они быстро бы перестали быть эталонными.

Но вообще внесение поправки – довольно редкий случай в практике измерений: это точные лабораторные измерения, научные исследования. Большей частью Δ_с есть, но её не выявляют для каждого данного экземпляра средств измерений. На множестве экземпляров данного типа средств измерений она проявляет себя, как случайная величина.

Таким образом, 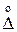проявляет себя, как случайная величина на множестве многократных наблюдений, если таковые производятся, а Δ_с проявляет себя, как случайная величина даже при одном измерении – на множестве экземпляров приборов данного типа.