Нормирование погрешностей

Нормируют предельно допускаемые значения погрешностей средств измерений, в первую очередь для основной погрешности. Существуют разные формы нормирования:

1) Нормируют предельно допускаемые значения основной приведённой погрешности, например, γ_о,п = ± 0,5 %. Так нормируют погрешности аналоговых вольтметров, амперметров и т.п. Это означает, что – 0,5 % ≤ γ_о ≤ 0,5 %.

Возможно, нам попался экземпляр прибора, у которого γ_о = 0, но мы этого не знаем. Мы знаем, что гарантируется – 0,5 % ≤ γ_о ≤ 0,5 %.

2) Гораздо реже гарантируется предельно допускаемые значения основной относительной погрешности, например, δ_о,п = ± 0,02 %. Так, например, нормируют погрешность измерительных мостов.

3) Нормируют предельно допускаемые значения основной относительной погрешности, но не в виде числа со знаками ±, а в виде формулы:

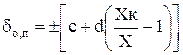. (13)

Так нормируют погрешность для цифровых измерительных приборов, например:

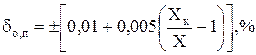
Дополнительные погрешности.

Классы точности

Класс точности – комплексная характеристика, которая говорит нам и об основной и о дополнительных погрешностях [9].

Обозначение классов точности:

· На циферблате аналогового прибора проставлено число, например, 0,5. Что оно означает? В первую очередь, что γ_о,п = ± 0,5 %.

· На лицевой панели прибора проставлено число внутри окружности, например,

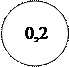
Это значит, что δ_о,п = ± 0,2 %.

· В документации цифрового измерительного прибора его класс точности обозначен 0,01/0,005. Это значит, что

.

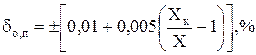Все числа, фигурирующие в обозначениях классов, выбираются из ряда

(1; 1,5; 2; 2,5; 4; 5; 6)·10^а,

где а = 1; 0; – 1; – 2; …

Кроме основной погрешности класс точности даёт информацию о дополнительных погрешностях, например, так, как это было показано в приведённых выше примерах, но как именно, в частности, «…не более половины основной…» или «…не более основной…» – это надо уточнять по документации на прибор.

Меры.

Первая характеристика меры – её номинальное значение Y_ном, для многозначной меры – множество номинальных значений.

Абсолютная погрешность меры: Δ = Y_ном – Y_ист ≈ Y_ном – Y_д, где Y_ист и Y_д - истинное и действительное значения меры.

Для однозначных мер относительная погрешность δ и приведённая погрешность γ – одно и то же, для многозначных соотношение между ними такое же, как у измерительных приборов.

Для тех и других сохраняются понятия систематической Δ_с и случайной 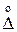составляющих.