Математическое моделирование и вычислительный эксперимент. Анализ ошибок. Устойчивость алгоритмов

История развития дисциплины «Методы вычислений»

Дисциплина "Методы вычислений" аккумулировала в себе алгоритмы построения приближенных решений различных математических задач современной математики: алгебры, математического анализа, дифференциальных и интегральных уравнений и др. Эти приближенные решения получают, как правило, в виде определенных числовых массивов, или в определенном численно-аналитическом виде. Конечно, возникают существенные вопросы качества приближенных решений: насколько они отличаются от искомых точных решений, какие факторы влияют на улучшение (ухудшение) ожидаемого приближенного результата и, в конце концов, как выполнять вычисления непосредственно.

Методы вычислений имеют долгую историю, которую можно условно разбить на три этапа. Первый этап – до Эпохи Возрождения – связан с необходимостью вычисления характеристик простых геометрических объектов (расстояние, углы, плошади, объемы и т.д.), расчетов простых механических устройств и систем, вычисления в астрономии. На этом этапе особенно отличился Архимед (287-212 гг. до н.э.). Известно, что именно он нашел отрезок числовой оси, в котором содержится число π, предоставил ему простые в практическом использовании пределы – ( 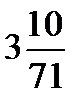; 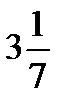) Относительная погрешность предложенного Архимедом приближенного значения числа π с этого отрезка составляет всего 0.04%. Поражает своей точностью достижения древнегреческого философа Гиппарх: 365 дней 5 часов 55 минут – такая по его вычислениям длина года на Земле. Это отличается от современных данных на 0.001%! Среди известных алгоритмов – алгоритм Евклида нахождения наибольшего общего делителя натуральных чисел: отнимать от большего меньше двух цифр пока они не сравняются.

Второй этап существенно меньше по размеру: от эпохи Возрождения до середины ХХ века. Но за каждым именем математиков того периода - шлейф выдающихся достижений! Ньютон, Эйлер, Лагранж, Гаусс, Леверье, Адамс, Бубнов, Галеркина, Крылов и другие. И этот список выдающихся имен далеко не полный. Их исследования стали весомым вкладом в вычислительную математику. Именно во втором периоде появился математический анализ, дифференциальные уравнения, что привело к возможности внедрения новых инженерных проектов из-за расчетов с высокой точностью.

Третий этап – с середины ХХ века до наших дней. Это этап постановки и решения нелинейных задач, отвечающих сложным математическим моделям процессов природы и технологий.

Объединяет все этапы так называемый главный метод приближенных вычислений, который можно описать на примере решения некоторого операторного уравнения

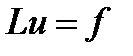(1)

где u - искомый элемент множества U, f - элемент множества F, оператор L: U →F. Предположим, что уравнение (1) имеет единственное решение u^*. Рассмотрим некоторое операторной уравнения

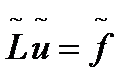(2)

для которого известно точное и единственное решение ^*, Причем 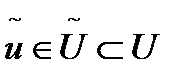, , 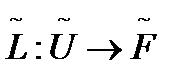. Будем считать, что уравнение (2) в каком-то смысле похоже на уравнение (1) (например, в уравнении (2) отсутствуют такие члены уравнения (1), от которых решение u мало зависит). Главный метод приближенных вычислений заключается в построении и решении такого уравнения (2), чтобы 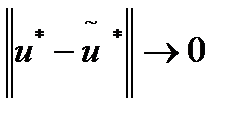. В этом случае в качестве решения уравнения (1) выбирают его приближенное решение – решение уравнения (2).