Погрешности вычислений

Понятие погрешностей вычислений изложены во многих пособиях по методам вычислений. Прежде всего известны понятия абсолютной и относительной погрешности числа. Абсолютной погрешностью 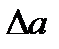числа a называется абсолютное значение разницы между данным числом и его приближенным значением 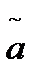, то есть 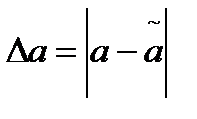. Относительной погрешностью δa числа a ≠0 называется отношение абсолютной погрешности 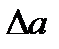к абсолютному значению числа a, то есть: .

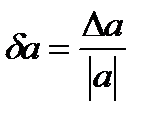При использовании приближенных чисел важно осознавать о конечной записи числа, что связано с понятием значимых и верных цифр. Значимой цифрой приближенного числа называется каждая цифра в его десятичной картинке включая нули между ненулевыми цифрами и нули справа от ненулевых цифр, но исключая нули перед первым ненулевым символом. Например, приближенная запись числа π ≅ 3.14159 содержит 6 значащих цифр, число 34000 содержит 5 значимых цифр, число 0.0034 содержит 2 значимые цифры. Такие же правила определения значимых цифр и для чисел, записанных в экспоненциальному виде. Цифра приближенного числа называется верной, если абсолютная погрешность этого числа не превышает половины единицы разряда, соответствующего этой цифре. Например, пусть дано точное число a =19.0547 и его приближенное значение 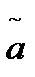= 19.0500. Здесь в записи приближенного значения числа 6 значащих цифр, из которых четыре – верные, так как | 19.0547-19.0500 | = 0.0047 <½0.01.

Методами дифференциального исчисления можно сформулировать основные правила вычисления погрешностей при осуществлении арифметических операций и элементарных функций над приближенными числами.

Погрешности вычислений по типу их происхождения можно представить тремя группами:

1. Неустранимые ошибки. Неустранимая погрешность является следствием: а) неточности исходных данных, входящих в математического описания задачи, б) несоответствия математической модели реальной задачи (иногда эту погрешность называют погрешностью математической модели).

2. Погрешности метода. Этот тип ошибок порожденный выбранным методом приближенного решения поставленной задачи, так как получение точного решения неограниченной или неприемлемо большого количества арифметических операций, а во многих случаях и просто невозможно.

3. Погрешности округления. Какой бы устройство-исполнитель вычислений не использовать – не избежать, вообще говоря, ошибок, связанных с ограничениями количества десятичных разрядов числа. Именно такое ограничение приводит к необходимости закругления чисел и, как результат, к соответствующим погрешностей.

В теории приближенных вычислений выделяют две задачи, которые соответственно называются прямой и обратной задачами теории погрешностей.

Прямая задача. Суть задачи: указано действия, которые следует выполнить над приближенными числами, и задано предельные погрешности входных данных. Нужно оценить погрешность результата.

Обратная задача. Суть задачи: указано действия, которые следует выполнить над приближенными числами, и задано максимально допустимую погрешность результата. Нужно установить, какими должны быть погрешности входных данных, чтобы полученный результат имел заданную степень точности.

Заметим, что эта задача, вообще говоря, имеет множество решений и поэтому является математически неопределенной. Для однозначности необходимо задать некоторые дополнительные условия.