Канонический анализ как метод исследования межгрупповой вариации
8.8 Канонический анализ имеет одно важное свойство, которое предоставляет значительные возможности для проведения антропологических исследований. Речь идет о его способности выявлять и описывать основные направления межгрупповой вариации наборов признаков.
Основное назначение этого метода заключается в решении задачи дискриминации и многие его свойства направлены на получение наилучшего разделения многомерных корреляционных эллипсоидов, включающих индивидуальные случаи, и обеспечение оптимальной работоспособности дискриминантных решающих правил. Вместе с тем, канонический анализ может применяться как метод решения классификационных задач. Действительно, способности канонических переменных наилучшим образом разделять сово-купности наблюдений могут также быть истолкованы как свойства этих переменных находить такие направления межгрупповой вариации, вдоль которых различия центральных точек выборок будут максимальными.
Иными словами, каждая каноническая переменная выявляет определенную ось, вдоль которой центральные точки некоторых выборок будут отстоять друг от друга так далеко, как это только возможно. Любая такая ось может считаться переменной, описывающей некоторое информативное направление межгрупповой вариации именно центральных точек выборок. При этом вариация индивидуальных наблюдений нас может специально и не интересовать. Таким образом, канонический анализ может считаться инструментом изучения межгрупповой вариации примерно так же как компонентный анализ позволяет рассматривать внутригрупповую изменчивость. Коэффициенты исходных признаков у канонических переменных позволяют интерпретировать морфологический смысл этих переменных и выяснять какие комплексы значений исходных признаков характерны для тех или иных групп выборок, локализованных на полюсах осей этих новых признаков.
Вторым важным свойством канонического анализа, которое позволяет его расценивать как метод решения задач классификации, является возможность наглядно представлять расположение центральных точек выборок в координатах канонических переменных. Такой график приведен на рисунке 8.3. Однако, на этой картине можно размещать только центральные точки выборок, не интересуясь при этом индивидуальными наблюдениями. Взаимное расположение одних только центральных точек позволит наглядно представить их пространственные взаимоотношения, наличие определенной структуры и т.д.
- 199 -
В третьих, канонический анализ позволяет выделить набор информативных признаков, выявляющих различия данного набора выборок наиболее отчетливо. Такое суждение можно сделать по значениям стандартизованных коэффициентов признаков у канони-ческих переменных. Очевидно, вклад каждого j-го признака в вариацию i-й канони-ческой переменной будет соответствовать его стандартизованному коэффициенту bij Аналогичный вклад этого признака в вариацию всех n канонических переменных может быть определен как сумма n его стандартизованных коэффициентов у всех этих переменных
gj = (b1j2 + b2j2 + b3j2 + ... + bnj2)1/2 . (8.23)
Суммирование квадратов значений bij необходимо для того, чтобы на величину gj не влияли различия в их знаках. С учетом равенства (8.17), связывающего стандартизованные bij и нестандартизованные cij коэффициенты bij = cijsj, величина gj может быть записана также в виде
gj = sj(c1j2 + c2j2 + c3j2 + ... + cnj2)1/2 . (8.24)
Очевидно, "ценные" исходные признаки будут характеризоваться большими значениями показателя gj.
8.9 Проведение канонического анализа может быть основано на решении уравнения
(SB - liSw)ci= 0.
Межгрупповую ковариационную матрицу можно получить из векторов средних Mi для разных выборок и Ni - объемов этих выборок. Эти данные всегда имеются в распо-ряжении исследователя. К тому же такая информация всегда содержится в научных публикациях. Все это позволяет включать в рассмотрение большие наборы групп наблю-дений, включающие десятки, сотни и даже тысячи выборок.
Вместе с тем, информация по внутригрупповым ковариационным матрицам Sw для большинства выборок обычно отсутствует. Аналогично, довольно редко и только в краниологических исследованиях публикуются индивидуальные наблюдения, по которым можно получить эти матрицы. Ситуация значительно облегчается тем обстоятельством, что для многих реальных случаев, возникающих в антропологической практике, внутригрупповые корреляционные матрицы оказываются весьма сходными, а некоторые наблюдаемые для них различия не обнаруживают конкретной антропологической специфики. Это, в частности, было показано для краниологических (Ефимова, 1991) и для соматологических признаков, используемых в расоведческих исследованиях (Дерябин, 1997). Значения внутригрупповых средних квадратических отклонений многих антропологических признаков также обнаруживают небольшие межгрупповые различия. Для краниологических показателей имеются даже стандартные их значения (Алексеев, Дебец, 1964), которые широко используются на практике.
Все это позволяет в качестве внутригрупповой ковариационной матрицы Sw пользоваться ее стандартными оценками для разных наборов признаков. Такие стандартные матрицы могут быть получены по нескольким (h) достаточно крупным выборкам. В каждой из них можно получить свою матрицу Swi с последующим их усреднением
N1Sw1 + N2Sw2 + N3Sw3 + ... + NhSwh
 Sw* = . (8.25)
Sw* = . (8.25)
N1 + N2 + N3 + ... + Nh
- 200 -
Разумеется, каждая из этих выборок должна быть заведомо однородной, и суммарный их объем должен составлять не менее 100-200 наблюдений.
Применение в уравнении (SB - liSw)ci= 0. стандартной внутригрупповой ковариационной матрицы Sw* позволит получить векторы ci для определения значений канонических переменных и корней li, являющихся межгрупповыми дисперсиями этих переменных. По векторам ci можно получить значение средней величины любой i-й канонической переменной Myij для каждой j-й выборки
Myij = ci'Mj, (8.26)
где Mj - вектор средних исходных признаков в j-й выборке. Эти средние Myij могут наноситься на различные графики, географические карты и т.д.
Вместе с тем, применение стандартной внутригрупповой ковариационной матрицы Sw* в уравнении канонического анализа, по-видимому, делает весьма приближенным применение статистического критерия проверки неслучайности величин корней li, что, впрочем, не слишком важно, так как основным свойством результатов такого анализа оказывается наглядность и интерпретируемость.
8.10 При использовании канонического анализа для решения некоторых антропологических задач может возникнуть проблема использования смешанного набора признаков, измеренных в разных шкалах. Такие шкалы сводимы к трем их классам: количественным, порядковым и номинальным. Шкалы первого типа характеризуются наличием бесконеч-но большого количества упорядоченных вариантов внутри области допустимых значений. В этих шкалах выражаются измерительные признаки. Шкалы второго типа имеют некоторое конечное (а для антропологических признаков - небольшое) количество дискретных вариантов, упорядоченных по степени проявления некоторого свойства. К этому типу признаков относятся многие антропоскопические балловые показатели, описывающие, например, рост бороды, положение кончика носа, и т.д., а также - цвет волос и глаз, если варианты пигментации сгруппированы в небольшое число градаций (3 или 5). Класс номинальных признаков предполагает существование некоторого количества дискретных и неупорядоченных вариантов. Примерами таких признаков могут являться форма нижнего края грушевидного отверстия или форма спинки носа, где последний вариант (изви-листая форма) не может считаться крайним проявлением некоторого качества, выраже-ние которого последовательно усиливается от первого к последнему состоянию.
При проведении канонического анализа, например, вариации расовых антропологических признаков современного населения возникает необходимость наряду с обычными измерительными показателями головы и лица использовать также важные антропоскопические свойства, описывающие пигментацию, характер волосяного покрова, строение мягких частей лица. Последняя группа признаков измеряется в порядковых и номинальных шкалах, что на первый взгляд затрудняет их одновременный анализ совместно с измерительными показателями.
Вместе с тем, три типа шкал измерения признаков имеют некоторые общие свойства. Во-первых, количественные признаки как измеряемые некоторыми инструментам могут одновременно считаться как непрерывно, так и дискретно варьирующими. Первым свойством они обладают, так как цена деления инструмента, теоретически говоря, может беспредельно уменьшаться. Однако, на практике используются приборы, проградуирован-
201 -
ные с точностью обычно до 1 мм, и варианты количественного признака оказываются по существу дискретными. Таким образом, для всех трех шкал признаков мы имеем дело с дискретными вариантами.
Во-вторых, номинальные признаки, имеющие неупорядоченные варианты, могут быть трансформированы в форму, которой свойственна их упорядоченность. Основой для этого является существование так называемых бинарных (дихотомических) признаков, обладающих только двумя вариантами, означающими наличие или отсутствие некоторого свойства. Если закодировать эти варианты баллами 0 и 1 или 1 и 2, или какими-либо иными несовпадающими количественными ярлыками, то бинарные признаки окажутся выраженными в порядковой шкале. Одновременно, номинальный признак, имеющий k неупорядоченных вариантов, легко может быть представлен в виде k - 1 бинарного признака (Бартлетт, 1968), каждый из которых будет иметь уже упорядоченные варианты. Такой перевод для k = 4 ниже показан в таблице, где неупорядоченные варианты обозначены через A, B, C и D, а получающиеся бинарные признаки - через X1, X2 и X3:
| A | B | C | D | |
| X1 | ||||
| X2 | ||||
| X3 |
Здесь первый бинарный признак X1 имеет два варианта: A, закодированный через 1 и объединение вариантов B, C и D, закодированное через 0. Аналогично, X2 выделяет вариант B с кодом 1 и объединение A, C, и D с кодом 0, X3 выделяет C, противопоставляя его группе вариантов A, B и D.
Например, для профиля спинки носа, имеющего четыре состояния, можно иметь три бинарных признака, описывающих встречаемость вогнутой, выпуклой и прямой форм. Каждый из этих новых признаков будет иметь по два состояния, соответственно оцифрованных баллом 0 (отсутствие встречаемости данного варианта профиля) и - 1 (присутствие этого варианта).
Следовательно, для всех трех шкал признаков существуют единые свойства - фактическая дискретность вариантов и либо естественная их упорядоченность, либо простые способы достижения этого. Поэтому, для любой переменной возможна форма представления вариации в виде таблицы стандартного вида:
| qi | q1 | q2 | q3 | ... | qk |
| ni | n1 | n2 | n3 | ... | nk |
совпадающей для количественных признаков с так называемым вариационным рядом. Здесь qi - код варианта признака, ni - количество наблюдений, имеющих этот вариант. Код варианта может быть либо выражен в естественных единицах измерения признака, либо являться принятым стандартным баллом. Если со значениями кодов для разных при-знаков работать как с обычными значениями количественных переменных, то для любого показателя по стандартным формулам можно получить среднюю арифметическую величину и среднее квадратическое отклонение. Для количественных признаков это будут
- 202 -
обычные статистические характеристики, для порядковых (балловых) переменных мы получим так называемый средний балл и балловое среднее квадратическое отклонение. Для бинарных признаков средняя арифметическая величина совпадет со значением доли варианта, закодированного баллом 1, то есть - с P = n1/N, а дисперсия, полученная по формуле, применяемой для количественных признаков, окажется той же самой, что и найденная по известной специальной формуле P(1-P). Средние арифметические величины Mi, найденные по единому способу вычислений для признаков с разной формой вариации, могут быть сведены в единый вектор средних M = [M1 M2 M3 ... Mn].
Аналогичным образом, для любой пары признаков по стандартной формуле можно найти коэффициент корреляции. Если оба признака - количественные, то эта формула даст обычный коэффициент прямолинейной корреляции, если обе переменные - бинарные, то мы автоматически получим величину четырехклеточного показателя связи, специально применяемого для этой ситуации. В том случае, когда один признак будет количественный, а другой бинарный, по стандартной формуле, применяемой к значениям кодов вариантов признаков, мы получим величину бисериального коэффициента корреляции. При сочетаниях двух балловых признаков или баллового показателя с количественной или бинарной переменной мы не придем к какой-то известной из теории статистики мере тесноты связей. Однако, и в этих случаях логический смысл и свойства коэффициента корреляции окажутся сохраненными. В этом последнем случае невозможно будет лишь проверять различные статистические гипотезы о существовании и величине связи. В результате мы сможем получить внутригрупповую корреляционную матрицу для признаков, измеренных в разных шкалах, но сведенных к единой форме варьирования с диск-ретными упорядоченными вариантами.
Пример 8.3 Рассмотрим проведение канонического анализа к решению классической антропологической задачи – исследованию расового состава населения некоторого региона. В качестве такого региона выберем зону Кавказа. Для нее имеются представительные результаты, полученные в ходе многолетних исследований антропологов: Г.Ф.Дебеца (1956), М.Г.Абдушелишвили (1964), А.Г.Гаджиева (1971), Р.М.Касимовой, (1975). Серия данных этих авторов включает 221 выборку. Рассматривались 22 признака, из которых 10 - измерительные, 12 антропоскопические.
При проведении канонического анализа было выделено несколько канонических переменных, первые две из которых, отражающие наиболее важные направления таксономической вариации, суммарно описывают 48% межгрупповой изменчивости исходных показателей (табл.8.5). Значения коэффициентов у исходных признаков для этих двух канонических переменных, позволяют оценить их морфологический смысл - то есть определить антропологические комплексы, соответствующие полюсам межгрупповой вариации. При подобном истолковании результатов канонического анализа следует обращать внимание только на те коэффициенты у признаков, которые имеют абсолютную величину, превышающую некотрый уровень (например - 0.2. Признаки с меньшими коэффициентами условно полагались малоценными и вносящими относительно небольшой вклад в значения соответствующей канонической переменной.
Первая каноническая переменная (табл.8.5) зависит, главным образом, от соотношения продольного и поперечного диаметров головы, которые имеют разные знаки для приве-
- 203 -
денных коэффициентов, а также - от встречаемости прямой формы волос, от цвета глаз и горизонтальной профилировки лица. В области своих малых величин первая каноническая переменная описывает комбинацию относительно длинной головы, уменьшения присутствия прямых волос, потемнения глаз и ослабления горизонтального профиля лица. Напротив, большие значения первой канонической переменной соответствуют комплексу брахикефалии, посветления глаз, увеличения частоты прямых волос и усиления горизонтальной профилировки лица.
На рисунке 8.4 представлено расположение центральных точек 221 выборки в осях первых двух дискриминаторов. На нем для обозначений точек, представляющих выборки, была использована их принадлежность к разным языковым семьям. Малым значениям первой канонической переменной соответствует компактный кластер, включающий ос-новную массу групп азербайджанцев, выборки курдов, татов-мусульман и будугцев, а также - лазаревских адыгейцев-шапсугов. Этому кластеру противостоит крупное объединение, включающее остальные группы народов Кавказа для которых характерны относи-
Таблица 8.5.Коэффициенты у исходных признаков для первых двух канонических переменных, найденных при анализе 221 выборки народов Кавказа
| Признаки | ||
| 1.Длина тела | 0.093 | -0.036 |
| 2.Продольный диаметр головы | -0.686 | 0.511 |
| 3.Поперечный диаметр головы | 0.650 | -0.400 |
| 4.Наименьшая ширина лба | 0.055 | -0.028 |
| 5.Морфологическ.высота лица | 0.061 | 0.114 |
| 6.Скуловой диаметр | 0.089 | 0.086 |
| 7.Нижнечелюстной диаметр | 0.073 | 0.182 |
| 8.Высота носа (от бровей) | -0.105 | -0.132 |
| 9.Ширина носа | 0.061 | 0.103 |
| 10.Высота верхней губы | -0.110 | -0.247 |
| 11.Цвет глаз | -0.269 | -0.289 |
| 12.Цвет волос | -0.024 | 0.167 |
| 13.Доля прямых волос | 0.347 | 0.419 |
| 14.Рост бороды | -0.036 | -0.110 |
| 15.Горизонтальный профиль лица | 0.223 | 0.383 |
| 16.Высота переносья | -0.162 | -0.153 |
| 17.Доля вогнутых спинок носа | 0.052 | 0.093 |
| 18.Доля выпуклых спинок носа | 0.096 | 0.102 |
| 19.Кончик носа | -0.024 | -0.183 |
| 20.Профиль верхней губы | 0.130 | 0.243 |
| 21.Наклон лба | 0.069 | 0.380 |
| 22.Развитие надбровья | 0.047 | 0.039 |
| Процент учитываемой вариации | 31.7 | 16.3 |
- 204 -
тельно большие величины первой канонической переменной. В области средних значений этого дискриминатора и больших величин второй канонической переменной без труда можно увидеть объединение групп адыгейцев: шапсугов тахтамукайских, бжедугов, чемгуев и абадзехов. Большим величинам второго дискриминатора (табл. 8.5) и этому кластеру соответствует комбинация увеличения относительной длины головы, уменьшения высоты более ортохейличной верхней губы, посветления цвета глаз, увеличения встречаемости прямых волос, усиления горизонтального профиля лица и ослабления наклона лба.
Таким образом, по результатам канонического анализа выявляются три морфологически достаточно отчетливо разделенных друг от друга антропологических варианта. Первый из выделенных вариантов соответствует хорошо известному каспийскому антропологическому типу индо-средиземноморской (или индо-афганской - в других классификациях) южной европеоидной расы. Второй кластер объединяет брахикефальные кавказские группы и соответствует местному варианту балкано-кавказской расы. Наконец, каноническим анализом объективно выявляется объединение четырех групп адыгейцев, к которому можно добавить и группу лазаревских адыгейцев-шапсугов, расположенную на графике (рис.8.4) поблизости от них и географически локализованную весьма далеко от ареала распространения каспийского антропологического типа, к зоне которого на рисунке 8.4 она близка. Этот третий кластер хорошо соответствует так называемому среднекубанскому антропологическому типу понтийской расы.
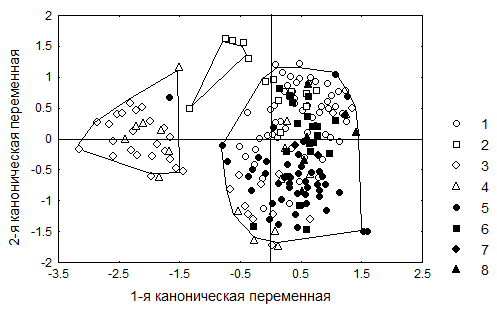 |
Рисунок 8.4. График средних значений первых двух канонических переменных в 221 выборке народов Кавказа Обозначения: 1 - картвельцы, 2 - абхазо-адыги, 3 - тюрки, 4 - иранцы, 5 - нахско-дагестанцы, 6 - армяне, 7 - греки, 8 - семиты
- 205 -
8.11 Канонический анализ может использоваться также и для решения классификационных задач в ситуации, когда выделение в имеющихся данных однородных групп индивидов - неочевидно. Это возникает, например, в случае рассмотрения механически смешанных данных, а также - в исследованиях в области эволюционной антропологии, когда рассматриваются отдельные палеоантропологические находки и установление таксономических взаимоотношений между нами являются целью проводимого анализа.
В таких ситуациях определение межгрупповой ковариационной матрицы SB невозможно, так как выделение относительно однородных совокупностей наблюдений, соответствующих таксонам, является целью исследования. Однако, в соответствии с разделом 2.6 в таких случаях по формуле (2.12) может быть получена так называемая общая матрица T, измеряющая суммарную изменчивость, проявляющуюся в материале. Для нее характерно то, что она в соответствии с формулой (2.15) может быть представлена в виде суммы T = B + W, где B - матрица, описывающая межгрупповую вариацию, W - аналогичная матрица внутригрупповой вариации. По W и B могут быть получены соответствующие ковариационные матрицы Sw= W/ (N - k) и SB = B / (k - 1). Аналогичным образом, и по T можно найти общую ковариационную матрицу
T
 ST = . (8.27)
ST = . (8.27)
N – 1
В ситуации изначальной неопределенности состава групп наблюдений матрицы T и ST всегда могут быть получены. Общая матрица ST неявно содержит в себе информацию о межгрупповой и внутригрупповой вариации. Первый компонент может быть выявлен при проведении канонического анализа, уравнением которого будет
(ST - li SW ) ci = 0 . (8.28)
Иными словами, в таком каноническом анализе рассматривается не межгрупповая вариация средних арифметических величин, которые можно получить только по результатам исследования, а изучается общая изменчивость всех индивидуальных данных. Для такого анализа внутригрупповая ковариацонная матрица SW может быть получена как некоторая стандартная оценка (8.25), опирающаяся на несколько заведомо однородных выборок. Она привнесет в канонический анализ информацию о величине и закономерностях внутригрупповой изменчивости, с которой будет сравниваться вариация в исследуемой совокупности индивидуальных наблюдений.
В результате решения уравнения (8.28) будут получены канонические переменные Yi, внутригрупповая вариация которых будет иметь простейшую форму: единичные дисперсии и нулевые взаимные корреляции. В общей вариации индивидуальных значений этих канонических переменных должны проявиться закономерности межгрупповой изменчивости. График оценок Yi для всех индивидуальных случаев может наглядно представить возможную межгрупповую структуру, существующую в общей вариации отдельных наблюдений.
Пример 8.4 Рассмотрим использование варианта канонического анализа для рассмотрения межгрупповых закономерностей вариации, проявляющихся в индивидуальной изменчивости отдельных наблюдений. Материалом послужили данные по размерам нейрокраниума ископаемых гоминид, принадлежащих видам: Homo erectus, Homo nean-
- 206 -
derthalensis и Homo sapiens (Алексеев, 1978). Рассматривались 10 признаков (табл.8.6) у 40 индивидуальных находок ископаемых гоминид, для которых можно было определить всю батарею показателей.
При проведении канонического анализа было выделено три канонических переменных, совместно описывающих соответственно 82,3% суммарной межгрупповой вариации признаков, что кажется вполне достаточным. Из таблицы 8.6 можно видеть, что первая каноническая переменная на полюсах своей вариации в области больших значений выделяет следующий комплекс признаков: большое значение диаметра gl-in, при относительном уменьшении продольного диаметра от op, уменьшение поперечного диаметра и высоты черепа при сильном развитии надбровья (разности диаметров gl-op и ophr-op), и относительно этих признаков повышенной емкости черепа. Малые значения канонической переменной характеризуются обратной комбинацией значений признаков. Иными словами, эта каноническая переменная учитывает определенный набор соотношений размеров мозговой части черепа.
Вторая каноническая переменная описывает соотношения двух групп признаков, первую из которых составляют емкость черепа и диаметра gl-in, вторую - продольный и поперечный диаметры черепа. Ее морфологический смысл не слишком ясен .
На рис.8.5 приведен такой график для сочетания первых двух канонических переменных, который отражает более 76% закономерностей рассматриваемой вариации. На нем видно, что вся совокупность точек графика легко может быть разделена двумя граничными линиями на три зоны. Первая из них включает неоантропов верхнего пале-олита. Нетрудно видеть, что Кафзех VI размещается в этой же зоне, что может соответствовать его оценке как одного из древнейших представителей Homo sapiens. Противоположная зона графика включает типичных представителей Homo erectus (Питекантроп I, Синантропы III, X, XII). Здесь же размещаются явантропы (Нгандонг V, XI) и так называемые пренеандертальцы (Брокен-Хилл, Салданья и Петралона). Последние по комплексу соотношений основных размеров нейрокраниума оказываются достаточно отделенными от палеоантропов, в группу которых они иногда включаются.
Таблица 8.6.Коэффициенты у признаков нейрокраниума гоминид для канонических переменных
| Признаки | |||
| 1.Емкость черепа | 0.96 | -1.43 | 0.18 |
| 2.Продольный диаметр | -1.72 | 1.46 | 0.25 |
| 3.Развитие надбровья | 0.68 | 0.11 | 0.34 |
| 4.Диаметр gl-in | 2.37 | -1.22 | -0.35 |
| 5.Поперечный диаметр | -1.66 | 1.46 | 0.46 |
| 6.Высота 22а | -1.08 | 0.18 | 0.23 |
| 7.Наименьший лобный диаметр | 0.33 | 0.12 | 0.65 |
| 8.Наибольший лобный диаметр | 0.37 | -0.72 | -0.09 |
| 9.Лобная дуга | -0.30 | 0.13 | -0.10 |
| 10.Теменная дуга | -0.30 | -0.05 | -0.17 |
| Доля изменчивости (%) | 56.5 | 19.7 | 6.1 |
- 207 -
В средней зоне графика размещаются палеоантропы - представители Homo neander-thalensis. Классические европейские формы (Монте-Чирчео, Ля-Шапелль-о-Сен, Ля-Ферраси, Спи I, Неандерталь, Ле-Мустье) располагаются ближе к линии, отделяющей палеоантропов от архантропов и пренеандертальцев. Лишь ювенильная форма Ле-Мустье, возможно, в силу незавершенности процессов матуризации, несколько сдвинута в направлении неоантропов. Палеоантропы Палестины и Передней Азии (особенно Схул IV и V, Шанидар I) размещены несколько ближе к линии, разделяющей палеоантропов и неоантропов.
Следует отметить, что размах значений канонических переменных - исключительно велик. Для первой такой переменной он составляет более 23, а для второй - более 16 значений внутригрупповых средних квадратических отклонений. Можно, вспомнить, что внутригрупповой размах значений любого признака обычно составляет 5 - 6 внутригрупповых "сигм". Для межгруппового внутривидового размаха (например, в рамках H.sapiens) точные значения такого размаха оценить трудно, но возможно, что они составляют аналогичные величины.
Тогда, представленная картина может соответствовать существованию 2 - 3 таксонов видового уровня. На рис.8.5 нетрудно также видеть, что по строению нейрокраниума известная точка зрения на возможность объединения палеоантропов и неоантропов в один вид Homo sapiens - слабо соответствует полученным результатам. Во всяком случае
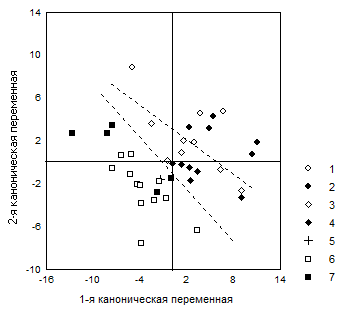 |
Рисунок 8.5. Расположение в осях первых двух канонических переменных вариантов нейрокраниума ископаемых гоминид. Обозначения: 1 - Homo erectus, 2 - пренеандертальцы, 3 - классические неандертальцы Европы, 4 – неандертальцы Передней Азии и Северной Африки, 5 - Кафзех VI, 6 - верхний палеолит Европы, 7 – верхний палеолит Азии и Африки
- 208 -
зоны графика, вмещающие представителей Homo erectus и пренеандертальцев с одной стороны, разные группы палеоантропов - с другой, и неоантропов с третьей - обнаруживают примерно одинаковую величину изменчивости.
8.12 Рассмотрение канонических переменных может считаться комбинацией методов компонентного и обычного дискриминантного анализов. Как в дискриминантном анализе здесь находятся новые переменные, имеющие предельно высокую степень межгруппового варьирования по отношению к внутригрупповой изменчивости. Способ нахождения этих признаков весьма похож на тот, который используется в анализе главных компонент, с той лишь разницей, что одновременно анализируются не одна, а - две ковариационные матрицы SB и Sw.
Сходство канонического и компонентного анализов может привести к тому, что возможность использования главных компонент, найденных для межгрупповой корреляционной матрицы, полученной по SB, будет расцениваться как дающая приемлемые резуль-таты. Этот прием широко использовался и используется в практике антропологических исследований. Рассмотрим правомочность такого подхода.
Каковы свойства межгрупповых дисперсий и корреляций? Основой одномерного однофакторного дисперсионного анализа является сравнение межгрупповой sB2 и внутригрупповой sw2 дисперсии с применением F-критерия Фишера. Здесь возможны две ситуации. Так, значения этих дисперсий могут быть очень близкими, так что sB2 » sw2. В этом случае можно сказать, что вариация средних арифметических величин - случайна. В ситуации, когда sB2 > sw2, можно сказать, что средние величины признака варьируют неслучайно. Таким образом, в общем случае можно считать, что межгрупповая дисперсия включает два компонента. Первый из них, неслучайный - определится "чистой" межгрупповой вариацией средних величин, второй - случайный, численно выражается внутригрупповой дисперсией. Когда неслучайный компонент изменчивости отсутствует, наблюдается sB2 » sw2. Таким образом, в составе межгрупповой дисперсии любого признака всегда в неявном виде присутствует внутригрупповой компонент вариации. Устранить его можно, только рассматривая одновременно обе дисперсии sB2 и sw2.
Примерно то же самое характерно и для межгрупповых корреляций. Известно, что, если изменчивость средних величин двух признаков в k выборках - случайна, то межгрупповой коэффициент корреляции совпадет по величине - с внутригрупповым. И только, когда эта вариация средних величин будет неслучайной, в составе межгруппового коэффициента корреляции появится дополнительная часть, которая будет определяться "чистыми" межвыборочными связями. Таким образом, и в составе межгрупповых коэффициентов корреляции всегда присутствует внутригрупповой компонент. Учесть его присутствие можно только рассматривая одновременно с межгрупповыми связями также и - внутригрупповые. По существу, на учете этого явлении основана известная рекомендация Е.М.Чепурковского (Tschepourkowsky,1905) одновременно рассматривать и межгрупповые и внутригрупповые корреляции с целью установления ценных для расоводиагностических целей признаков.
Из сказанного ясно, что рассмотрение одной лишь межгрупповой изменчивости, описываемой дисперсиями или коэффициентами корреляции, найденными на основе средних арифметических величин - недостаточно, так как в ней всегда неявно будет присут-
- 209 -
ствовать определенный внутригрупповой компонент, который по смыслу любого таксономического анализа следует устранить. Канонический анализ как раз и позволяет сделать это, так как в нем одновременно рассматриваются два уровня вариации: межгрупповой, описываемый межвыборочными дисперсиями и ковариациями признаков, и внутригрупповой, где используются аналогичные внутривыборочные характеристики.
На иных посылках основан компонентный анализ. Здесь предполагается существование только одного уровня изменчивости, для которого следует найти закономерности коррелированности признаков. Уравнение этого анализа имеет вид (R - liI) ai = 0, где R - рассматриваемая корреляционная матрица. По существу, здесь реальные коэффициенты корреляции, входящие в матрицу R, сравниваются с так называемой единичной матрицей I, которая является моделью ситуации, когда все признаки не скоррелированы друг с другом. Использование компонентного анализа для изучения межгрупповой вариации, когда наборы средних величин для разных признаков считаются как бы соответствующими наборам величин признаков у индивидов, по существу означает, что исследователь сознательно закрывает глаза на факт внутригрупповой вариации, допуская тем самым недопустимый произвол.
Метод главных компонент в соответствии с своими свойствами предназначен для рассмотрения внутригрупповой вариации, изучаемой в однородных группах населения. При этом единицей исследования оказывается индивид. Но можно ли представить себе ситуацию, когда компонентный анализ межгрупповой корреляционной матрицы, найденной по средним величинам, даст совершенно те же самые результаты, что и канонический анализ? Для ответа на этот вопрос достаточно немного преобразовать формулу канонического анализа к следующему виду
(KRBK- liRw) ci = 0, (8.29)
где RBи Rw - межгрупповая и внутригрупповая корреляционные матрицы, а матрица
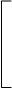
 sB1/sw1 0 0 ... 0
sB1/sw1 0 0 ... 0
0 sB2/sw2 0 ... 0
K = 0 0 sB3/sw3 ... 0 (8.30)
... ... ... ... ...
0 0 0 ... sBm/swm
включает отношения межгрупповых и внутригрупповых средних квадратических отклонений всех признаков. Таким образом, для того, чтобы формулы компонентного и канонического анализа совпали бы, и оба этих анализа дали бы одни и те же результаты, требуется одновременное соблюдение двух условий. Во-первых, внутригрупповые корреляции все признаков должны быть нулевыми, и тогда внутригрупповая корреляционная матрица Rw будет равна единичной матрице I. Во-вторых, должно соблюдаться K = I, то есть - на главной диагонали матрицы K должны стоять единицы, что будет означать равенство межгрупповых и внутригрупповых дисперсий для всех признаков. Но последнее условие означает полное отсутствие неслучайной межгрупповой вариации. Иными словами, два метода анализа дадут одинаковые результаты лишь в ситуации, когда никакой межгрупповой вариации наблюдаться не будет, а рассмотрению будет подвергаться только внутригрупповая вариабельность.
В реальных ситуациях компонентный анализ межгрупповой корреляционной матрицы выявит закономерности вариации, в которых одновременно будут присутствовать два
- 210 -
различных компонента: "чистый" межгрупповой и случайностный внутригрупповой. Первый из них - содержательно интересен, второй можно считать своего рода "статистическим шумом". Обе этих части вариации будут представлены в смешанном виде, и истолкование межгрупповых главных компонент как отражающих "чистые" межгрупповые закономерности связей признаков не всегда может быть обоснованным.
Вместе в тем, в ряде случаев использования межгрупповых главных компонент соотношение "чистой" межгрупповой и внутригрупповой частей в исследуемой вариации может сложиться таким, что первая окажется преобладающей. Тогда можно будет надеяться на то, что результаты компонентного анализа опишут преимущественно межгрупповые закономерности вариации и дадут картину, очень сходную с получаемой на основе канонических переменных. Однако, в реальных ситуациях никогда невозможно сказать насколько результаты компонентного анализа близки к тем, которые можно было бы ожидать от использования канонических переменных.
Пример 8.5 Рассмотрим данные примера 8.4 с использованием главных компонент. Здесь будут исследоваться отдельные индивидуальные наблюдения, и без учета сказанного в предыдущем разделе может показаться, что компонентный анализ является подходящим инструментом их рассмотрения. В примере 8.4 эти материалы подверглись каноническому анализу. Насколько иначе главные компоненты опишут рассматриваемую таксономическую вариацию?
Нагрузки признаков нейрокраниума ископаемых гоминид на главные компоненты приведены в таблице 8.7. Можно видеть, что для первой из них наблюдаются положительные связи практически со всеми размерами, за исключением развития надбровья. Таким образом, первая главная компонента описывает обычно получаемый при проведении компонентного анализа внутригрупповой вариабельности индивидуальных наблюдений результат. Она является характеристикой общей величины нейрокраниума. Лишь развитие надбровья в вариации этого показателя участвует слабо. Если сравнить нагрузки на первую главную компоненту, полученную в этом примере (табл.8.7), с аналогичными нагрузками на первый главный фактор, найденными в примере 6.6 (табл.6.7), можно видеть очевидное сходство их структуры. Однако, во втором случае изучалась именно внутригрупповая вариация признаков черепа. Поэтому, можно сказать, что компонентный анализ признаков нейрокраниума у ископаемых гоминид в качестве наиболее важного направления вариации выявил нечто очень похожее на обычно находимую закономерность внутригрупповой вариации общей величины мозговой части черепа. На ее полюсах выделяются просто крупные и просто небольшие по своим размерам черепа. Этот результат не вызывает удивления, так как присутствие внутригрупповой вариации в рассматриваемых данных - несомненно и устранить ее можно только одновременным рассмотрением общей и внутригрупповой изменчивости. Канонический же анализ, который позволяет сделать это, в качестве наиболее важной закономерности вариации выделил вовсе не изменчивость общей величины признаков, а - вариацию определенных соотношений размеров нейрокраниума (табл.8.6).
График сочетаний значений первых двух главных компонент (рис.8.6) обнаруживает определенное сходство с аналогичной картиной, полученной для двух канонических переменных (рис. 8.5). Здесь также можно обнаружить те же самые три зоны, включа-
- 211 -
Таблица 8.7. Нагрузки у признаков нейрокраниума гоминид для главных компонент
| Признаки | |||
| 1.Емкость черепа | 0.89 | -0.17 | 0.01 |
| 2.Продольный диаметр | 0.57 | 0.71 | 0.32 |
| 3.Развитие надбровья | -0.35 | 0.85 | 0.12 |
| 4.Диаметр gl-in | 0.38 | 0.78 | 0.40 |
| 5.Поперечный диаметр | 0.54 | 0.55 | -0.49 |
| 6.Высота 22а | 0.79 | -0.55 | 0.07 |
| 7.Наим.лобный диам. | 0.74 | 0.33 | -0.40 |
| 8.Наиб.лобный диам. | 0.88 | 0.07 | -0.21 |
| 9.Лобная дуга | 0.68 | -0.17 | 0.25 |
| 10.Теменная дуга | 0.70 | -0.45 | 0.32 |
| Описываемая доля изменчивости (%) | 45.8 | 28.0 | 8.8 |
ющие неоантропов, палеоантропов и архантропов с пренеандертальцами. Правда, линия, разделяющая архантропов и пренеандертальцев от неандертальцев носит криволинейный, и поэтому, несколько искусственный характер. Однако, на этом графике можно отметить возможность разделения представителей Homo erectus от пренеандертальцев. Последние оказываются заметно ближе к неандертальцам чем архантропы.
Таким образом, график первых двух главных компонент, несколько отличаясь от аналогичной картины, полученной при помощи канонического анализа, может, на первый взгляд, считаться также достаточно логичным. Правда, следует заметить, что величина таксономических различий на этом графике не может быть оценена из-за свойств компонентного анализа. Размахи значений первых двух главных компонент составляют около 5 значений средних квадратических отклонений, вычисленных для всех рассмотренных наблюдений. Эти "сигмы" не могут быть истолкованы ни как внутригрупповые, ни как межгрупповые. По существу, они описывают стандартную величину изменчивости, которую можно найти для любой группы наблюдений, в том числе и для сборной выборки, включающей гоминид разного таксономического уровня.
Сравнивая результаты, полученные с применением канонического и компонентного анализа можно также отметить следующее. Канонические переменные четко выявляют существование трех морфологических таксонов: неоантропов, палеоантропов и архантропов с пренеандертальцами. Картина, выявляемая компонентным анализом, дает менее отчетливые результаты. Но и здесь можно говорить о существовании трех морфологических вариантов.
График первых двух главных компонент демонстрирует практически трехполюсное взаимоотношение выделенных вариантов. По существу, здесь можно видеть, что архантропы отличаются от неоантропов примерно в той же степени, как последние отстоят от основной массы палеоантропов и пренеандертальцев. По результатам же канонического анализа палеоантропы были морфологически промежуточными между архантропами и неоантропами.
Какая картина более точно выявляет реальные взаимоотношения индивидуальных вариантов в соответствии с выделенными направлениями таксономической вариации? Ес-
- 212 -
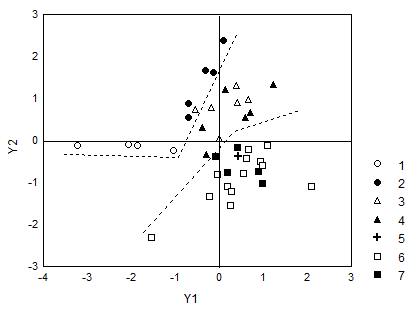 |
Рисунок 8.6. Расположение в осях первых двух главных компонент вариантов нейрокраниума ископаемых гоминид. Обозначения: 1 - Homo erectus, 2 - пренеандертальцы, 3 - классические неандертальцы Европы, 4 – неандертальцы Передней Азии и Северной Африки, 5 - Кафзех VI, 6 - верхний палеолит Европы, 7 – верхний палеолит Азии и Африки
ли даже не учитывать соображений о методической корректности канонического анализа и о слабой обоснованности использования здесь главных компонент, и о выявлении первой главной компонентой по существу внутригруппового направления изменчивости, дополнительное основание для выбора может дать рассмотрение этих же данных с применением некоего третьего способа анализа. В примере 10.2 (глава 10) данные по размерам нейрокраниума ископаемых гоминид рассмотрены с использованием метода многомерного шкалирования, который основан на совершенно иных математических соображениях по сравнению с каноническим и компонентным анализами. Результаты шкалирования (рис. 10.4) практически идентичны тем, которые были получены в каноническом анализе и заметно отличаются от картины для главных компонент. Поэтому, можно сделать вывод о том, что на рисунке 8.6 представлена картина, где таксономические взаимоотношения вариантов искажены неадекватно использованным методом анализа.
8.13 Доступная литература по каноническому анализу - невелика. Простое изложение содержится в статье М.С.Бартлетта (1968), и соответствующий раздел в книге В.Ю.Урбаха (1972). Дискриминантные возможности этого метода описаны в книге Дж.Кима и др.(1989). Результаты применения канонического анализа для решения задач классификации можно найти, например, в работах В.Е.Дерябина (1997, 1998, 1998а, 1999).
Дата добавления: 2016-02-13; просмотров: 3440;
