Канонические дискриминантные функции
Канонический дискриминантный анализ
8.1 В дискриминантном анализе k рассматриваемых совокупностей решающие правила основывались на применении k функций, каждая из которых позволяла определить возможность отнесения некоторого наблюдения к каждой из этих совокупностей. Возможен иной ход анализа, когда пытаются построить дискриминантные функции, которые смогут разделять сразу несколько совокупностей друг от друга. Пусть, например, имеется три совокупности наблюдений - w1, w2 и w3, корреляционные эллипсы которых расположены в осях двух исходных признаков X1 и X2 так, как это показано на рисунке 8.1. Можно видеть, что нетрудно провести ось нового признака Y1, которая разделит зону вариации w1 от аналогичной зоны w2. Этот новый признак может считаться дискриминантной функцией, разделяющей первые две совокупности наблюдений. Однако, он никак не позволяет отделить w1 и w2 от w3. Чтобы это можно было осуществить, следует провести ось другого нового признака Y2, по значениям которой корреляционный эллипс для w3 достаточно надежно отделяется от аналогичных эллипсов для w1 и w2. Ось второго нового признака, который также является дискриминантной функцией, можно провести так чтобы координаты Y1 и Y2 были взаимно перпендикулярными. Рассмотренный гипотетический пример иллюстрирует основную идею так называемого канонического дискриминантного анализа.
Канонические дискриминантные функции
8.2 Итак, пусть мы имеем k совокупностей w1, w2, ... , wk, в каждой из которых опреде-лен вектор средних Mi и ковариационная матрица Si. Пусть также ковариационные матрицы во всех этих совокупностях не различаются S1 = S2 = S3 = ... =Sk = Sw. Необходимо построить набор n дискриминантных функций (n < k), которые должны разделить все эти совокупности максимально хорошо.
Эти дискриминантные функции могут быть найдены как линейные комбинации набора исходных признаков X
Y1 = c1'X
Y2 = c2'X
Y3 = c3'X
... …
Yn = cn'X
Для того, чтобы они обладали дискриминантными возможностями, для каждой из них должно соблюдаться условие (7.12), согласно которому отношение
(Величина межгрупповой изменчивости)
 L = = max .
L = = max .
(Величина внутригрупповой изменчивости)
Величина внутригрупповой вариации каждого из n новых признаков может быть измерена его дисперсией
swyi2 = ci' Sw ci . (8.1)
Так же как внутригрупповая вариабельность набора исходных признаков описывается внутригрупповой ковариационной матрицей, межгрупповую изменчивость можно
- 188 -
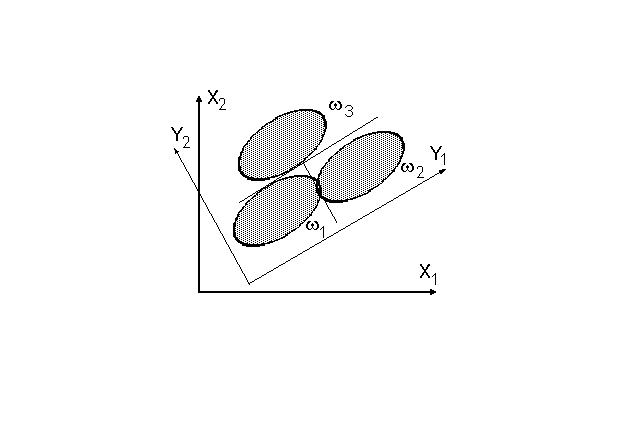
Рисунок 8.1.Построение двух дискриминантных функций Y1 и Y2, разделяющих три совокупности наблюдений w1, w2 и w3
охарактеризовать межгрупповой ковариационной матрицей, зависящей от вариации векторов средних Mi. Эта матрица была описана в разделе 2.6 и имеет вид
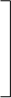
 sB11 sB12 sB13 ... sB1m
sB11 sB12 sB13 ... sB1m
sB12 sB22 sB23 ... sB2m
SB = sB13 sB23 sB33 ... sB3m ,
... ... ... ... ...
sB1 m sB1 m sB1 m ... sB m m
где диагональные элементы оказываются межгрупповыми дисперсиями одномерного дисперсионного анализа
1 k
 sBff = S Ni(Mif - Mof)2 ,
sBff = S Ni(Mif - Mof)2 ,
k - 1 i = 1
а внедиагональные элементы являются межгрупповыми ковариациями
1 k
 sBfh = S Ni(Mif - Mof) (Mih - Moh),
sBfh = S Ni(Mif - Mof) (Mih - Moh),
k - 1 i = 1
Мерой межгрупповой изменчивости каждого i-го нового признака Yi служит его межгрупповая дисперсия
- 189 -
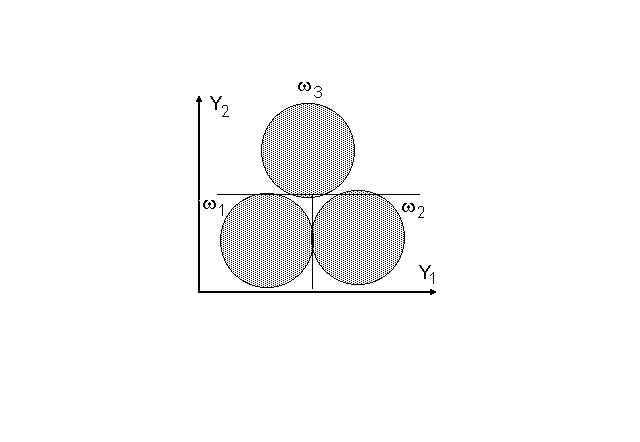
Рисунок 8.2. Расположение корреляционных эллипсов трех совокупностей наблюдений w1, w2 и w3 в осях двух дискриминантных функций Y1 и Y2
sByi2 = ci' SB ci. (8.2)
Тогда условие того, чтобы каждая переменная Yi являлась бы дискриминантной функцией, можно выписать в виде
sByi2 ci' SB ci

 L = = = max . (8.3)
L = = = max . (8.3)
sWyi2 ci' SW ci
Кроме этого, было бы желательным, чтобы в межгрупповом плане все новые при-знаки Y1, Y2, ..., Yn были бы взаимно нескоррелированными. Это означает, что диск-риминантные функции должны иметь межгрупповую ковариационную матрицу диагонального вида

 sBy12 0 0 ... 0
sBy12 0 0 ... 0
0 sBy22 0 ... 0
SBy = 0 0 sBy32 ... 0 . (8.4)
... ... ... ... ...
0 0 0 ... sByn2
Весьма удобно также, чтобы во внутригрупповом плане новые признаки имели бы простейшую форму варьирования, т.е. - были бы взаимно некоррелированными и имели бы внутригрупповые дисперсии равные 1. Для этого должно выполняться условие
- 190 -
Swy = C' Sw C= I ,
где Swy - внутригрупповая ковариационная матрица новых признаков, матрица C включает все векторы c1, c12, ..., cn, а I - единичная матрица.
Простая форма варьирования означает, что в системе координат новых переменных Yi корреляционные эллипсоиды превратятся в многомерные сферы. Эта ситуация для гипотетического примера, изображенного на рисунке 8.1, приведена на рисунке 8.2.
Таким образом, искомые дискриминантные функции должны обладать тремя свойствами: максимизировать отношение (8.3), иметь нулевые межгрупповые корреляции и простейшую форму внутригрупповой изменчивости. Такие новые переменные называются каноническими дискриминантными функциями или просто - каноническими переменными. Способ их получения называется каноническим дискриминантным анализом или просто – каноническим анализом.
8.3 В многомерной статистике доказывается, что перечисленные желательные свойства новых признаков Yi будут характерными, если векторы c1, c12, ..., cn для их получения в виде Yi = ci' X, будут найдены из уравнения
SB ci = li Sw ci , (8.5)
которое также можно переписать в виде
(SB - li Sw) ci = 0 . (8.6)
Это уравнение будет иметь решение, если определитель
½SB - li Sw ½ = 0 (8.7)
Этот определитель в своем развернутом виде преобразуется к уравнению n-й степени относительно неизвестных чисел l. Его решением является n корней l1, l2, l3, ..., ln. Подставляя в уравнение (8.6) каждый из этих корней, можно последовательно получить векторы c1, c12, ..., cn .
Уравнение (8.7) имеет n корней. Если число исходных признаков Xj (m) оказывается меньше числа рассматриваемых групп наблюдений без одного (k - 1), то n = m. Эта ситуация понятна по аналогии с методом главных компонент, где решается сходное уравнение ½S - lI½ = 0, и число новых переменных было равно числу исходных признаков. Однако, если m > k - 1, то количество корней и соответствующих им канонических переменных определяется уже количеством групп наблюдений без одной, т.е. - n = k - 1. Эта ситуация требует объяснения.
Действительно, если мы имеем только две группы (k = 2), то их центральные точки могут быть расположены на прямой линии, которой соответствует только одна функция, необходимая для их дискриминации. В случае трех групп наблюдений ( k = 3) их центральные точки можно расположить на плоскости, задаваемой осями двух канонических переменных (рис.8.2). Для размещения же центров четырех совокупностей наблюдений, понадобится трехмерное дискриминантное пространство и т.д. В общем случае k групп понадобится пространство k - 1 измерения, которому будут соответствовать k - 1 канони-ческая дискриминантная ось.
Из уравнения (8.6) в соответствии с разделом А.28 Приложения А, следует, в частности, выполнение
C'SBC= L , (8.8)
где матрица L включает корни уравнения (8.7)
- 191 -

 l1 0 0 ... 0
l1 0 0 ... 0
0 l2 0 ... 0
L = 0 0 l3 ... 0 .
... ... ... ... ...
0 0 0 ... ln
С другой стороны, эта формула в соответствии с разделом 1.13, означает получение межгрупповой ковариационной матрицы набора новых признаков (8.4). Иными словами,
L = SBy . (8.9)
Таким образом, числа li, являющиеся корнями уравнения (8.7), оказываются значениями межгрупповых дисперсий канонических переменных, так что l1 = sBy12, l2 = sBy22, l3 = sBy32, ..., ln = sByn2.
Решение уравнений (8.6) и (8.7) может быть осуществлено несколькими способами, один из которых описан в разделе В.6 Приложения В.
8.4 В практике проведения канонического дискриминантного анализа вычисления часто проводятся не для ковариационных матриц SB и SW, а - для лежащих в их основе матриц сумм
B = (k - 1)SB (8.10)
W = (N - k)SW ,
где N = SNi - суммарное количество наблюдений в k выборках. Матрицы B и W были подробно нами описаны в разделе 2.6. Это те же самые матрицы, которые используются в критерии Уилкса (см.раздел 2.7).
Уравнения (8.6) и (8.7) в этом случае приобретают вид
(B - fi W) vi = 0 .
½B - fi W½= 0 (8.11)
Корни последнего из них достаточно просто соотносятся с числами li, получаемыми из уравнения (8.7)
k - 1
 fi = li , (8.12)
fi = li , (8.12)
N - k
а векторы vi и ci связаны простым равенством
ci = vi (N - k)1/2 . (8.13)
При проведении вычислений корни fi (или li) обычно находятся в упорядоченном виде, так что соблюдается неравенство f1 > f2 > f3 > ... > fn или l1 > l2 > l3> ... > ln. Это означает, что первая каноническая переменная Y1 имеет наибольшую межгрупповую дисперсию и описывает тем самым наиболее важное направление межгрупповой вариации. Вторая каноническая переменная Y2 имеет вторую по величине межгрупповую дисперсию и опи-сывает, таким образом, вторую по степени важности закономерность межвыборочной изменчивости и т.д. Здесь наблюдается аналогия с тем, что мы имели в компонентном анализе, с той лишь разницей, что главные компоненты описывали не межгрупповые закономерности изменчивости признаков, а - внутригрупповые.
По корням fi в каноническом анализе часто вычисляются так называемые канонические корреляции
- 192 -

 fi 1/2
fi 1/2
 Ri = . (8.14)
Ri = . (8.14)
1 + fi
Каждая из них измеряет коррелированность набора исходных признаков с группами наблюдений. Смысл этой корреляции можно представить себе как связь набора показателей X c некоторым качественным признаком g, вариантами которого являются номера выборок 1, 2, 3, ..., n. Коэффициенты канонической корреляции также упорядочены по их значениям, так что выполняется неравенство R1 > R2 > R3> ... > Rn. Таким образом, первой и самой важной канонической переменной соответствует наибольшая каноническая корреляция, второй такой переменной - вторая по величине каноническая связь и т.д.
Кроме значений векторов ci, при помощи которых можно получать индивидуальные оценки дискриминантных функций Yi = ci' X, где X включает обычные (ненормированные) значения признаков, часто вычисляются также стандартизованные величины этих векторов bi, позволяющие делать то же самое по нормированным величинам zi = (Xi - Mi)/si, имеющим нулевую среднюю и единичную дисперсию. Стандартизованные значения векторов, получаются в виде
bi = ciV, (8.15)
где матрица
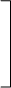
 s1 0 0 ... 0
s1 0 0 ... 0
0 s2 0 ... 0
V = 0 0 s3 ... 0 . (8.16)
... ... ... ... ...
0 0 0 ... sn
включает внутригрупповые средние квадратические отклонения исходных признаков sj. Каждый j-й элемент i-го стандартизованного вектора bi, соответствующий j-му исходному признаку, может быть найден из формулы
bij = cij sj . (8.17)
Стандартизованные векторы позволяют по величине составляющих их элементов определять относительный вклад каждого признака в ту или иную каноническую переменную, описывающую определенную закономерность межгрупповой изменчивости признаков.
Значения канонических переменных Yi = сi' X часто вычисляются в центрированном виде, так чтобы для каждой из них общая средняя величина, найденная по всем N1 + N2 + +... + Nk наблюдениям, была бы равна нулю. Для достижения этого для каждой такой переменной находится константа Yoi = ci' Mo, где Mo - вектор общих средних исходных признаков, найденных суммарно для всех наблюдений по векторам средних Mi в отдельных выборках
N1M1 + N2M2 + N3M3 + ... + NkMk
 Mo = .
Mo = .
N1 + N2 + N3 + ... + Nk
Центрированные значения дискриминантных функций у j-го наблюдения находятся в виде
yij = Yij - Yoi.
Кроме этого в каноническом анализе часто вычисляются нагрузки исходных признаков на канонические переменные, являющиеся коэффициентами корреляции признаков и этих переменных. Вектор таких нагрузок rki может быть получен по формуле
- 193 -
rki = Rw bi , (8.18)
где Rw - внутригрупповая корреляционная матрица, полученная для аналогичной ковариационной матрицы Sw. Наборы нагрузок могут использоваться для интерпретации смысла канонических переменных примерно таким же образом, как это можно было сделать для главных компонент или факторов.
8.5 Аналогично тому, как это было характерно для главных компонент, для каждой канонической переменной можно определить долю межгрупповой вариации исходных признаков, которая учитывается этой переменной. Такой показатель легко получить в виде
li fi

 Pi = = . (8.19)
Pi = = . (8.19)
l1 + l2 + ... + ln f1 + f2 + ... + fn
Кроме этого на основе величин корней l1 , l2 , ... , ln был построен статистический критерий, позволяющий проверить предположение о случайности их значений. Пусть по k выборкам с суммарным объемом N = N1 + N2 + ... + Nk при проведении канонического анализа были получены n корней f1, f2, f3, ..., fn. Так как соблюдается неравенство f1> f2 > >f3 > ... > fn, несколько последних чисел могут оказаться настолько малыми, чтобы возникли сомнения в их неслучайности. Иными словами, следует проверить предположение о том, что соответствующая им межгрупповая дисперсия неотлична от нуля. Проверка этого предположения осуществляется пошаговым образом.
Сначала проверяется наличие в составе выделенных корней хотя бы одного из них, величина которого отличается от нуля. Для этой цели применяется критерий Бартлетта

 m + k n
m + k n
 M = (N - 1) - ln P (1 + fi) , (8.20)
M = (N - 1) - ln P (1 + fi) , (8.20)
2 i = 1
Он очень похож на критерий значимости (4.22), применявшийся к каноническим корреляциям. Распределение M критерия в ситуации, когда заведомо все n корней не отличаются от нуля, близко к распределению c2 с числом степеней свободы n = m (k - 1). Если M > > cо2, где cо2 - табличная его величина, то по меньшей мере один, самый крупный по своей величине корень fi, может считаться неслучайным и описывающим какой-то действи-тельно объективно имеющийся компонент межгрупповой вариации. Если M < cо2 проверка показывает отсутствие какой-либо неслучайной межгрупповой вариации. Компьютерные программы выводят P вероятность ошибки 1-го рода, соответствующую найденному значению критерия M. Если P < a (0.05, 0.01, 0.001), нулевая гипотеза отвергается, и тем самым признается, что по крайней мере первая каноническая корреляция неслучайно отличается от нуля. Если P > a, нулевая гипотеза сохраняется, и проверка прекращается.
При обнаружении с использованием критерия (8.20) неслучайности величины первого корня f1 проверка продолжается, и проверяется предположение о равенстве нулю остальных корней f2, f3, ..., fn. Для этой цели применяется критерий

 m + k n
m + k n
 M = (N - 1) - ln P (1 + fi) , (8.21)
M = (N - 1) - ln P (1 + fi) , (8.21)
2 i = 2
- 194 -
который имеет распределение c2 с числом степеней свободы n = (m - 1) (k - 2). Если M > > cо2, где cо2 - табличная его величина, то неслучайность значений и второго корня f2 считается доказанной и проверка продолжается. Последовательно проверяются предположения о равенстве нулю наборов корней f3, f4, ..., fn; затем - f4, f5, ..., fn и т.д. Критерий для такой проверки в общем случае имеет вид

 m + k n
m + k n
 M = (N - 1) - ln P (1 + fi) , (8.22)
M = (N - 1) - ln P (1 + fi) , (8.22)
2 i = q+1
где q - количество корней, для которых уже доказана неслучайность их величины. Критерий имеет распределение c2 с числом степеней свободы n = (m - q) (k - q - 1).
8.6 С использованием значений n дискриминантных функций Yi = ci' X можно постро-ить дискриминантные решающие правила, соответствующие им классификационные таблицы и др. Это можно осуществить стандартным образом, описанным в предыдущей главе, с той лишь разницей, что вместо рассмотрения индивидуальных наборов m исходных признаков X1, X2, X3, ..., Xm в k выборках, дискриминантному анализу подвергаются индивидуальные батареи n значений канонических переменных Y1, Y2, Y3, ..., Yn.
Работоспособность решающих дискриминантных правил, основанных на канонических переменных, часто бывает несколько худшей по сравнению с аналогичными правилами, разработанными для исходных переменных. Причина этого заключается в том, что часто несколько последних канонических переменных исключаются из рассмотрения вследствие того, что статистическая проверка не позволила установить неслучайность их межгрупповой вариации, т.е. неслучайность соответствующих им чисел fi. Из-за этого может иметь место потеря информации о межгрупповой вариации, присутствующей в k выборках.
Вместе с тем, канонический анализ обладает важным преимуществом по сравнению с обычным получением дискриминантных решающих правил для исходных признаков. Это преимущество заключается в том, что в осях канонических переменных можно наглядно представить основные закономерности межгрупповой вариации. Для этого можно построить графики, в которых на плоскостях, образованных осями разных пар канонических переменных Y1 и Y2, Y1 и Y3, Y2 и Y3, будут нанесены точки, соответствующие их индивидуальным значениям. В результате на этих графиках можно будет увидеть взаимное расположение "облаков" этих точек, соответствующих разным выборкам, степень трансгрессии этих "облаков" и т.д.
Поэтому, проведение канонического анализа обычно бывает направлено на выявление основных закономерностей межвыборочной вариации и наглядное их представление в графическом виде. При этом дополнительно обычным способом, описанным в главе 7, находятся системы дискриминантных функций для исходных признаков.
Пример 8.1 Проведем канонический анализ для трех краниологических серий, относящихся к средневековым восточным славянам-вятичам. Первая из них характеризует группы вятичей, расселенные в верхнем течении р.Москвы и ее притока - Истры, вторая - относится к вятичам среднего течения этой реки, третья - характеризует племена нижнего течения Москвы и бассейн р.Пахры. Эти данные мы использовали в примере
- 195 -
Таблица 8.1. Значения корней дискриминантных функций, соответствующих им канонических корреляций и проверка их случайности
| Корни | Каноничес-кие корреляции | Критерий Бартлетта | n | P |
| 0.529 | 0.588 | 30.323 | 0.016 | |
| 0.409 | 0.538 | 13.545 | 0.059 |
7.1, где были найдены дискриминантные функции по исходным признакам. В таблице 8.1 приведены значения корней уравнения (8.12) и соответствующих им канонических корреляций. Так как рассматриваются три выборки (k = 3), выделены только две канонические переменные (n = k - 1). Можно сказать, что первая закономерность межгруппо-вой вариации набора рассматриваемых признаков скоррелирована с рассматриваемыми выборками вятичей с коэффициентом 0.59. Аналогичная каноническая связь для второй закономерности межгрупповой вариации имеет лишь немного меньшую тесноту, численно выражаемую коэффициентом корреляции 0.54.
Применение критерия Бартлетта для проверки случайности величин корней (табл. 8.1) позволяет обнаружить неслучайный характер первой из них (P = 0.016 < 0.05) и констатировать недоказанность второй закономерности вариации (P = 0.059 > 0.05). Правда, вероятность ошибки 1-го рода для второго корня лишь немного превышает критический уровень (0.05), и вряд ли на основе этого следует формально отвергать возможность существования второго направления межгрупповой вариации.
В таблице 8.2 приведены нестандартизованные и стандартизованные коэффициенты для определения значений двух канонических переменных. Таблица 8.3 содержит также нагрузки исходных признаков на канонические переменные, по которым можно определить смысл выделенных канонических переменных. Первая из этих переменных заметно и
Таблица 8.2. Нестандартизованные и стандартизованные коэффициенты канонических переменных
| Признаки | Нестандартизованные значения | Стандартизованные значения | ||
| 1 Продольный диаметр черепа | 0.003 | 0.068 | 0.031 | 0.535 |
| 8 Поперечный диаметр черепа | -0.182 | -0.128 | -0.803 | -0.566 |
| 45 Скуловой диаметр | 0.173 | -0.109 | 0.840 | -0.531 |
| 48 Верхняя высота лица | -0.076 | 0.068 | -0.335 | 0.298 |
| 54 Ширина грушевидного отверстия | 0.275 | 0.352 | 0.448 | 0.573 |
| 751 Угол выступания носа | 0.028 | -0.099 | 0.165 | -0.578 |
| 77 Назомалярный угол | 0.031 | 0.109 | 0.169 | 0.592 |
| ZM Зигомаксиллярный угол | -0.042 | -0.001 | -0.213 | -0.038 |
- 196 -
положительно скоррелирована с продольным диаметром черепа, скуловым диаметром и шириной грушевидного отверстия. Отрицательные корреляции у этого нового признака можно найти для поперечного диаметра черепа и назомалярного угла. Таким образом, большие значения первой канонической переменной можно обнаружить для сочетания уменьшения черепного указателя и назомалярного угла, увеличения скулового диаметра и ширины грушевидного отверстия. Обратная комбинация большей величины черепного указателя и назомаляного угла, узколицести и узконосости будет характеризоваться малыми значениями первой канонической переменной.
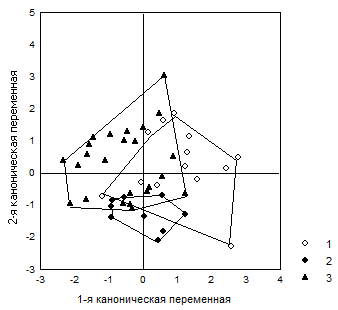
По графику индивидуальных значений двух канонических переменных (рис.8.3) можно видеть, что комплекс признаков, свойственный большим величинам первой из них, характерен для вятичей верховий р.Москвы и ее притока - Истры. Напротив, малые зна-чения первой канонической переменной проявляются у вятичей нижнего течения р.Мос-квы и бассейна р.Пахры.
Таблица 8.3. Нагрузки исходных признаков на канонические переменные
| Признаки | ||
| 1 Продольный диаметр черепа | 0.376 | 0.257 |
| 8 Поперечный диаметр черепа | -0.389 | -0.303 |
| 45 Скуловой диаметр | 0.633 | -0.283 |
| 48 Верхняя высота лица | -0.192 | 0.165 |
| 54 Ширина грушевидного отверстия | 0.476 | 0.265 |
| 751 Угол выступания носа | 0.179 | -0.557 |
| 77 Назомалярный угол | -0.318 | 0.253 |
| ZM Зигомаксиллярный угол | -0.246 | 0.086 |
На этом графике также можно видеть, что группа вятичей среднего течения р.Москвы выделяется малыми значениями второй канонической переменной, для которых (табл. 8.3) характерна комбинация увеличения черепного указателя при относительном (не абсолютном) увеличении угла выступания носа и уменьшении назомалярного угла.
8.7 Канонический дискриминантный анализ может использоваться также в качестве метода изучения множественных связей между набором количественных переменных X1, X2 , X3, ..., Xm и некоторым качественным признаком Q, имеющим k упорядоченных или неупорядоченных градаций. Действительно, пусть для 1-го, 2-го, ... , k-го варианта признака Q характерно присутствие у N1, N2, ..., Nk наблюдений. Тогда можно считать, что мы имеем дело с k выборками, имеющими эти численности. В ходе канонического анализа этих k выборок можно будет получить канонические корреляции, каждая из которых может рассматриваться как описывающая некоторый аспект связей между набором количественных признаков Xi и качественным признаком Q. Рассмотрение нагрузок на полученные канонические переменные позволит выяснить какие из количественных признаков наиболее тесно связаны с показателем Q.
 |
- 197 -
Рисунок 8.3. График индивидуальных значений первых двух канонических переменных в трех краниологических сериях средневековых славян-вятичей
Пример 8.2 Рассмотрим коррелированность размеров тела с наличием или отсутствием menarche у 14-летних девочек. Для этой цели использовались данные продольно-попе-речных обследований детей г.Москвы (Соловьева и др., 1977). Рассматривались 11 размеров тела. Наличие или отсутствие menarche кодировалось значениями 1 или 0 качественного признака. Количество наблюдений в выборке составило N = 103.
Таблица.8.4.Нагрузки размеров тела на каноническую переменную для определения их связи с наличием menarche
| Признаки | |
| Длина корпуса | 0.696 |
| Длина ноги | 0.485 |
| Длина руки | 0.473 |
| Акромиальный диаметр | 0.619 |
| Тазогребневой диаметр | 0.646 |
| Жировая складка под лопаткой | 0.529 |
| Жировая складка на трицепсе | 0.438 |
| Жировая складка на животе | 0.583 |
| Обхват бедра | 0.723 |
| Обхват груди | 0.816 |
| Обхват плеча | 0.622 |
- 198 -
Канонический анализ выделил одну переменную, при проверке случайности величины которой было найдено значение критерия 46.187, что при числе степеней свободы 11 обеспечивает c вероятность. ошибки 1-го рода P = 0.00 отклонение предположения о случайности вариации размеров тела в зависимости от наличия menarche. Величина канонической корреляции равна 0.619, что позволяет констатировать наличие значительной связи между размерами тела и наличием menarche. При рассмотрении нагрузок размеров тела на каноническую переменную (табл.8.4) можно найти, что наиболее тесно с наличием menarche связаны обхваты груди и бедра, длина корпуса и тазогребневой диаметр. Длина конечностей и жировые складки с наличием menarche связаны заметно меньше.
Дата добавления: 2016-02-13; просмотров: 2152;
