Умови рівноваги між фазами
В умовах термодинамічної рівноваги хімічний потенціал компонента однаковий в кожній фазі гетерогенної системи, тобто
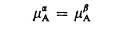 , (5.5)
, (5.5)
адже для однокомпонентної системи хімічний потенціал дорівнює потенціалу Гіббса,
Gі = μі (5.6)
а в умовах рівноваги потенціали Гіббса обох фаз рівні
G1 = G2 (5.7)
Якщо хімічний потенціал компонента в одній з фаз зміниться і буде відрізнятися від хімічного потенціалу цього ж компоненту у другій фазі, термодинамічний потенціал системи збільшиться, і в системі починається процес перерозподілу компоненту між фазами, що викликатиме пониження термодинамічного потенціалу системи. І буде він йти до того часу, доки хімічні потенціали компоненту у фазах не вирівняються.
Таким чином, хімічний потенціал компонента у всіх фазах рівноважної системи рівний. У загальному випадку можна записати
mai = mbi (5.8)
Ми вже знаємо, що потенціал Гіббса системи залежить від температури, тиску і концентрації компонентів:
dG = -SdT + vdp + Smidхi (5.9)
Для однокомпонентної системи
хі = 1, dхi = 0, (5.10)
тоді
dG = -SdT + vdp (5.11)
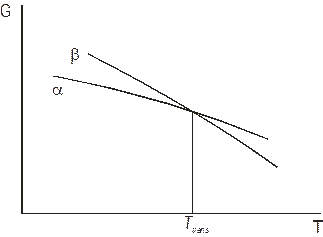
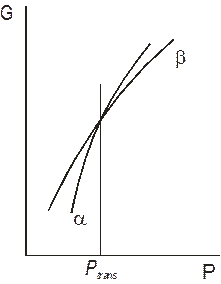
Графічно залежність потенціалу Гіббса системи від температури представляється кривою, що спадає, від тиску – кривою, що зростає. Якщо система містить дві фази, кожна фаза матиме свою залежність, як показано на рис. 5.1 і 5.2. В точках Тtrans і Ptrans криві перетинаються. Отже, в цих точках Ga= Gb. В області зліва від Тtrans і Ptrans стабільною є фаза a, адже її потенціал Гіббса менший, справа від Тtrans і Ptrans стабільною є фаза b.
| 
|
| Рис. 5.1. Температурні залежності потенціалів Гіббса фаз a і b. | Рис. 5.2. Залежності потенціалів Гіббса фаз a і b від тиску. |
Для кожної фази можна записати рівняння (5.11):
dGa = -SadT + VadP та dGb = -SbdT + VbdP (5.12)
При рівновазі
dGa = dGb, або -SadT + vadp = -SbdT + vbdp, (5.13)
тоді (Sb – Sa)dT = (vb – va)dp (5.14)
або 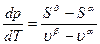 =
= 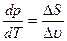 . (5.15)
. (5.15)
З іншого боку, dG = dH –TdS (5.16)
При рівновазі dG = 0 і dH = TdS, (5.17)
А оскільки процес відбувається зворотно,
DН = ТDS (5.18)
Підставляємо DS в (5.15), отримуємо
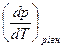 =
= 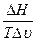 (5.19)
(5.19)
Це рівняння називається рівнянням Клапейрона – Клаузіуса. Воно є загальним і застосовне до всіх двофазних рівноваг і відповідних фазових переходів і показує залежність рівноважного тиску від температури. Геометричний образ цього рівняння – лінії. Подивимось, як вони виглядають.
Застосуємо рівняння Клаузіуса - Клапейрона до рівноваги між твердою фазою і рідиною, DH буде зміною молярної ентальпії або молярною теплотою плавлення (часто позначають L), а Dv буде зміною молярного об’єму при плавленні.
Величина DH завжди позитивна і вважаємо, що не залежить від температури. Насправді DH залежить від температури через теплоємність (с = Н/Т), але ця залежність настільки незначна, що нею можна нехтувати. В цьому випадку рівняння (5.19) є рівнянням прямої. Подивимось, який її нахил. Зміна об’єму Dv може бути позитивною, або негативною. Тому пряма плавлення може мати позитивний чи негативний нахил. Зазвичай об’єм рідини більше об’єму твердої фази (vl – vs = Dv > 0) і пряма має позитивний нахил. У зворотному випадку, як для металічних вісмуту і галію, води вона має негативний нахил.
Візьмемо оборотний вираз до рівняння (5.19), який покаже залежність температури фазового перетворення від тиску:
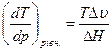 . (5.20)
. (5.20)
Нехай Dv=0, тоді перетворення відбувається при постійній температурі. Отже в координатах Т – р воно буде виражатися вертикальною прямою. При Dv > 0 пряма відхилена від вертикального положення вправо, при Dv < 0 – вліво.
При плавленні теплота поглинається, і DН > 0. Тоді при Dvпер>0 i зростанні тиску (Dp >0) температура фазового перетворення буде зростати (пряма відхилена вправо, а при DVпер< 0 зростання тиску буде викликати пониження температури фазового перетворення (відхилена вліво), що ілюструє добре відомий всім факт пониження температури плавлення води при підвищенні тиску. Це відхилення незначне, адже при значному збільшенні тиску температура плавлення збільшується незначно.
Застосуємо рівняння Клапейрона – Клаузіуса до рівноваг із парою – випаровування, сублімація. При цьому Dv ≫ 0, адже об’єм пари значно більший, ніж рідини і твердого тіла. Тоді рівняння (5.19) можна переписати як
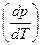 =
= 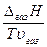 . (5.21)
. (5.21)
DгазН – ентальпія випаровування або сублімації, її часто позначають l.
В першому наближенні газ можна розглядати як ідеальний, для якого виконується рівняння рv = RT i 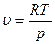 . (5.22)
. (5.22)
Підставляємо в (5.21), отримуємо
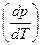 =
= 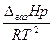 , або
, або 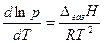 , або
, або 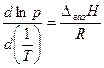 (5.23)
(5.23)
Якщо DгазН не залежить від температури, після інтегрування матимемо:
lnр = - 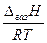 (5.24)
(5.24)
або
p = 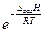 (5.25)
(5.25)
Рівняння (5.25) показує експоненційну залежність тиску пари від температури, тобто відповідні геометричні образи, які є кривими випаровування і сублімації, мають експонентну форму.
Рівняння (5.24) дає можливість графічно визначати ентальпію перетворення (випаровування або сублімації) з графіку lnp – 1/T. Нахил кривої при заданій температурі дає значення -DгазH/R.
Обидві криві і пряма плавлення перетинаються в точці, яка відповідає трифазній рівновазі тверда фаза – рідина – газ. Таким чином, ми теоретичнопобудували діаграму стану однокомпонентної системи. Її показано на рис. 5.3.
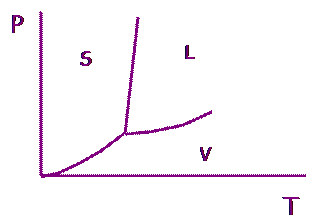
| Рис. 5.3. Діаграма стану однокомпонентної системи. S – тверда фаза, L – рідка фаза, V – газова фаза. |
Точка перетину трьох кривих називається потрійною точкою. Поблизу неї крива «рідина – газ» має менший нахил, ніж «тверда фаза – газ», адже ентальпія сублімації має більше значення, ніж ентальпія випаровування.
Тепер, коли ми вже знаємо, які є термодинамічні функції і що таке хімічний потенціал, давайте застосуємо ці знання до однокомпонентної системи. Подивимося, скільки фаз можуть знаходитись у рівновазі в однокомпонентній системі. Для цього спершу нам треба отримати правило, яке пов’язує кількість компонентів у системі з кількістю фаз у рівновазі. Це є правило фаз Гіббса, яке було виведене Дж. В. Гіббсом у 1876 р. Воно справедливе для систем із будь-якою кількістю компонентів.
Правило фаз Гіббса
Ми щойно записали умови хімічної рівноваги: mai = mbi . Ми також знаємо, що для того, щоб відбувалася термодинамічна рівновага, система має також перебувати в стані термічної і механічної рівноваги. Нехай ми маємо систему, яка містить k компонентів і f фаз. Запишемо всі умови рівноваги:
 |  | ||
Т(1) = Т(2) = Т(3) = … = Т(f) умова термічної рівноваги 2 Загальне
р(1) = р(2) = р(3) = … = р(f) умова механічної рівноваги число

 зміних
зміних
x1(1) + x2(1) + x3(1) + ... + xk(1) = 1 ∑xi(j)=1 k f+2
. . . . . . . . . . . . . . . . . . . f
x1(f) + x2(f) + x3(f) + ... + xk(f) = 1
Загальне
 число
число
m1(1) = m1(2) = m1(3) = ... = m1(f) Для кожного рівнянь
m2(1) = m2(2) = m2(3) = ... = m2(f) компонента k(f-1) +f
m3(1) = m3(2) = m3(3) = ... = m3(f) в кожній фазі
. . . . . . . . . . . . . . . . . . mі(j) = m0 + RTlnai(j)
mk(1) = mk(2) = mk(3) = ... = mk(f) Кількість рівнянь:
k (f-1)
Нижній індекс відноситься до номера компонента, верхній – до номера фази. Рівності Т(1) = Т(2) і т.д. і р(1) = р(2) і т.д. є тотожностями, m1(1) = m1(2) – рівняннями. Кожне рівняння типу m1(1) = m1(2) зв’язує змінні, які характеризують гетерогенну систему.
З кусу математики відомо, що число незалежних змінних дорівнює загальному числу змінних мінус число рівнянь, що їх зв'язують.
Загальне число змінних буде
n = k f + 2 (5.26)
Число рівнянь становить:
m =k(f-1) + f (5.27)
Число незалежних змінних, або число ступенів свободи, або варіантність:
n = kf + 2 - [k (f - 1) +f] = kf + 2 – kf + k – f
n= k – f + 2 (5.28)
Це рівняння називають правилом фаз Гіббса. n – число ступенів свободи. Воно показує, скільки змінних можна довільно змінювати, щоб число фаз залишилося незмінним.
Тепер, коли ми вже знаємо, які є термодинамічні функції і що таке хімічний потенціал, давайте застосуємо ці знання до однокомпонентних систем.
Правило фаз говорить нам, що в рівновазі можуть перебувати одна, дві та три фази, адже n не може бути менше 0. Порахуємо можливості.
n = k – f + 2
k = 1 завжди
f = 1 n = 1 – 1 + 2 = 2 система біваріантна
f = 2 n = 1 – 2 + 2 = 1 система моноваріантна
f = 3 n = 1 – 3 + 2 = 0 система інваріантна
f = 4 n = 1 – 4 + 2 = -1 неможливий випадок
Отже, в рівновагах можуть перебувати від однієї до трьох фаз. Якщо у метала тільки одна алотропна модифікація (Al, Cu та інш.), ці три фази – тверда, рідка і газова.
Поняття про ФІзико-хімічний аналіз
Фізико-хімічний аналіз – це комплекс експериментальних методів дослідження речовин – диференціальний термічний аналіз (ДТА), рентгенівський фазовий аналіз (РФА), мікроструктурний аналіз (МСА), локальний рентгеноспектральний аналіз (ЛРСА) та інші. ДТА дає інформацію про температури фазових перетворень; РФА – про фази, які спостерігаються у певному зразку; МСА – про первинну фазу і наявність структурних складових (евтектик), про кількість фаз та їх морфологію, про послідовність процесів при охолодженні зразків; ЛРСА – про хімічний склад певних фаз та евтектик.
Фізико-хімічний аналіз вивчає залежності між складом і властивостями макроскопічних систем, складених з декількох вихідних речовин (компонентів). При цьому ці залежності представляють графічно, у вигляді діаграми склад-властивість; застосовують також таблиці числових даних і аналітичні вирази. Залежності, які представлені графічно у вигляді діаграми “склад – властивість”, називають хімічними діаграмами. Приклад такої показано на рис. 5.4.
Властивості системи можуть залежати не тільки від її складу, але й від інших факторів, що визначають стан системи, наприклад, від тиску, температури, ступеня дисперсності, напруженості гравитаційного і електромагнітного полів, часу спостереження тощо. В цьому випадку будують діаграми «фактор рівноваги – властивість». Такі діаграми називають фізико-хімічними діаграмами.
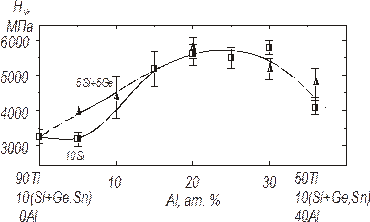
Рис. 5.4. Залежність твердості евтектики від вмісту алюмінію в три- та чотирикомпонентних сплавах Ti-10Si-Al та Ti-5Si-5Ge-Al.
поняття про геометричну термодинаміку.
На відміну від хімічної діаграми, фазова діаграма встановлює залежності між параметрами, які характеризують стан системи. На цих діаграмах всі хімічні процеси, що відбуваються в системі при зміні будь-якого фактора рівноваги (утворення і розпад хімічної сполуки, поява і зникнення твердих та рідких розчинів і т. і.), виражаються як геометричні зміни комплексу ліній, поверхонь і точок, що утворюють діаграму. Тому аналіз геометрії діаграм дозволяє робити висновки про відповідні процеси в системі. Графічне зображення гетерогенних процесів і рівноваг, що базується на строгих закономірностях, відрізняється більшою наочністю. Цими питаннями займається самостійний розділ термодинаміки, який має назву геометричної термодинаміки.
Графічне тлумачення зміни характеристичних термодинамічних функцій в залежності від параметрів стану і встановлення на цій основі закономірних графічних співвідношень між ними лежить в основі вчення про діаграми стану гетерогенних систем. Діаграма стану, діаграма фазових рівноваг, фазова діаграма – це графічне відображення функціональних залежностей склад – властивість, отриманих на основі комплексного дослідження системи. Вона однозначно описує рівноважні стани фізико-хімічної системи як функцію внутрішніх і зовнішніх параметрів. Діаграми стану відбивають вплив внутрішніх і зовнішніх параметрів на агрегатний стан системи, залежність фазового і хімічного складу фаз від температури тощо.
Таким чином, діаграмою стану називають графічне зображення співвідношень між параметрами стану. Іншими словами, діаграма стану – це геометричний образ термодинаміки взаємодії компонентів і, відтак, є об’єктом геометричної термодинаміки.
Кожна точка на діаграмі стану має назву фігуративної точки і визначає числові значення параметрів, що характеризують даний стан системи. Діаграма стану є однією з хімічних діаграм. Будь-яка точка діаграми стану, незалежно від місця її розташування, має фізичне значення, тому що відповідає певному стану системи. Діаграма стану дає відповідь на питання про те, скільки і які конкретно фази утворюють систему при даних значеннях параметрів стану. Яка інформація міститься у фазовій діаграмі?
· Про стабільність фаз у залежності від зовнішніх і внутрішніх параметрів і, відтак, про фазовий стан системи.
· Про характер і температуру фазових перетворень і, відтак, про температурні області існування фаз.
· Про розчинність компонентів у фазах при різних температурах і, відтак, про концентраційні області існування фаз.
Отже, діаграма стану акумулює обширну термодинамічну інформацію.
Дата добавления: 2016-02-27; просмотров: 1840;
