Фазові діаграми однокомпонентних систем

Стан однокомпонентної системи однозначно визначається набором двох параметрів (тиск і температура, тиск і об’єм, об’єм і температура). Для кожної з фаз системи будь-яка властивість змінюється безперервно при зміні обраних двох параметрів, утворюючи поверхню. Ці поверхні називають характеристичними або фігуративними, а кожна точка на поверхні називається фігуративною і відображує стан системи (властивість) при заданому наборі параметрів. Кожній фазі відповідає своя поверхня. Поверхні перехрещуються вздовж лінії, яка відповідає співіснуванню двох фаз. Лінії перехрещуються в точці, в якій співіснують три фази. Як ми вже знаємо, більше трьох фаз в однокомпонентній системі співіснувати не можуть.

Зазвичай параметрами однокомпонентної системи обирають температуру і тиск. Загальне рівняння термодинамічного потенціалу для кожної з фаз тоді буде виглядати як

G = f (T, p) (5.29)

При геометричному зображенні це потребує тримірних образів, що незручно. Тому діаграми стану однокомпонентних систем представляють у координатах T – p (або Т – V, p – V). В залежності від координат, їх ще називають T – p діаграми, Т – V діаграми, p – V діаграми. В таких проекціях вони мають вигляд плоских зірок.

Рис. 5.6 дає приклад діаграми стану однокомпонентної системи в координатах T – p. Бачимо, що є три області, кожна з яких представляє одну гомогенну фазу – рідку, тверду або парову. Правило фаз показує, що однофазні області в унарній системі мають два ступені свободи. Таким чином, в такій області можна одночасно варіювати і температуру, і тиск за умови, звичайно, залишатися в межах області, згідно з принципом неперервності. Для твердої фази – в межах площі, обмеженої кривими OA, OC, і віссю тиску. Області з двома ступенями свободи називається біваріантними.

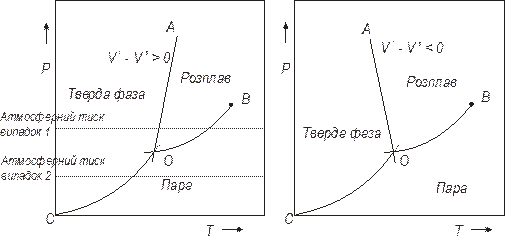
Рис. 5.6. р –Т діаграма однокомпонентної системи.

Окрім однофазних областей (однофазна рівновага), на діаграмі присутні лінії, які визначають двофазні рівноваги:

l ⇌ s співіснування рідкої і твердої фаз

l ⇌ v співіснування рідкої і парової фаз

s ⇌ v співіснування твердої і парової фаз

Для них n = 1 – 2 + 2, n = 1. Рівновага двох фаз в унарній системі має одну ступінь свободи. Це означає, що ми можемо довільно змінювати одну із змінних – тиск або температуру. Вибравши цю змінну, інша буде змінюватися згідно з функціональною залежністю між ними. На рис. 5.6 це пряма ОА (рівновага між рідкою і твердою фазами) та криві OB (l ⇌ v) і OC (s ⇌ v). Області з одним ступенем свободи називають моноваріантними.

Нарешті, криві перехрещуються в точці О. Немає ступенів свободи або, звичайною мовою, система інваріантна. Це твердження означає, що співіснування трьох фаз в унарній системі може відбутися лише при фіксованих температурі і тиску на діаграмі P – T (рис. 5.6).

Бачимо, що на рис. 5.6а нахил прямої ОА позитивний (більшість речовин), на рис. 5.6б – негативний (вода, вісмут, галій), пов’язаний зі зменшенням об’єму при плавленні.

Між кутовими коефіцієнтами ліній в потрійній точці існує співвідношення: 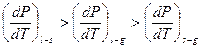. Значить існують метастабільні продовження кривих – між іншими двома. Вони показані пунктиром.

Для більшості металів тиск у потрійній точці значно нижче атмосферного тиску. Це означає, що такі метали при нагріванні при атмосферному тиску плавляться коли температура сягає кривої ОА і потім киплять, коли крива OB буде досягнута. Деякі метали, такі як миш'як, мають потрійну точку значно вище атмосферного тиску. При нагріванні при атмосферному тиску такі метали досягають кривої ОС і перетворюються з твердого стану в пар сублімацією. Кожен з процесів відбувається ізотермічно. Всі вони є зворотними.

Рис. 5.7 показує реальну р –Т діаграму води. Звернемо увагу, що крива рівноваги рідкої води зі своєю насиченою парою має продовження в область твердого льоду (крива ST). Ця крива показує рівновагу переохолодженої води зі своєю парою. Ця рівновага метастабільна. Напроти, продовження кривої сублімації в область високих температур (рівновага перегрітого льоду з насиченою парою, АТ) відсутня адже тверде тіло неможна перегріти, воно розплавиться.

Важливо ще сказати про точку С. В цій точці рідину і пар розрізнити неможна, ентальпія перетворення прямує до 0. Точка називається критичною і є нонваріантно.

З газу в рідину можна перейти двома шляхами:

1. Ізотермічно ® підвищення тиску ® через фазове перетворення «пара – рідина». Зворотний перехід.

2. Неізотермічно ® підвищення температури вище точки В ® підвищення тиску ® охолодження. Незворотний перехід. Точку С можна обійти.

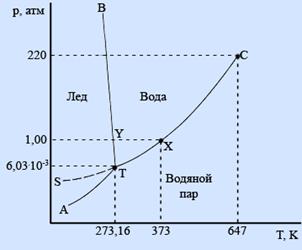
Рис. 5.7. р –Т діаграма води.   Потрійна точка води відповідає стану з Р = 6.1 кПа, Т = 273.16 К. Температура плавлення води нижче за потрійну точку і становить 273.15 К при атмосферному тиску.

Ми розглянули випадок, коли речовина має тільки одну алотропну форму. Якщо їх більше, всі вони мають знайти своє місце на діаграмі стану, згідно з правилом відповідності. Діаграма ускладнюється. Наприклад, фрагмент фазової діаграми води в області високих тисків і низьких температур, де існують різні модифікації льоду показаний на рис. 5.8, на рис. 5.9 – кристалічна структура різних модифікацій льоду.

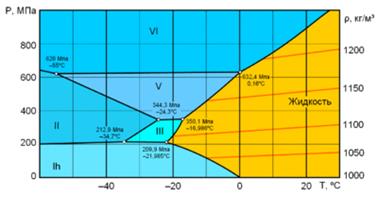
Рис. 5.8 Діаграма стану води при високих тисках і низьких температурах.

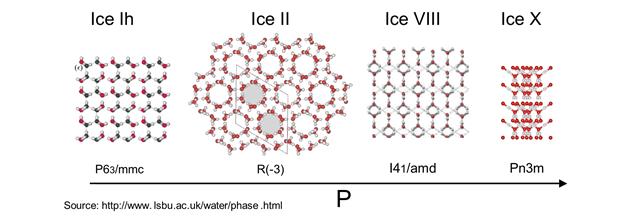
Рис. 5.9 Кристалічна структура різних модифікацій льоду.

Відповідно до відносної стабільності фаз у поліморфних речовинах, поліморфні перетворення можуть бути енантіотропними і монотропними. Що це таке? Розглянемо зміну термодинамічного потенціалу з температурою.

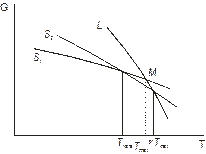
Випадок 1. Рис. 5.10 а. Енантіотропія. G = f (T, p) Нижче температури перетворення стабільна фаза S₁, далі до температури плавлення – S₂, вище температури плавлення – рідина. Але поверхні G = f (T, p) всіх фаз перехрещуються, отже можливі переходи S₁ « S₂ « L, які є зворотними. Хоча деякі можуть бути метастабільні – плавлення S₁. Це, згідно з принципом відповідності, має бути відображено в діаграмі стану, рис. 5.11.

а	б	в

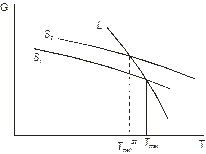
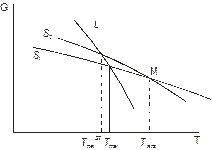
Рис. 5.10. Термодинамічні умови енантіотропних і монотропних перетворень.

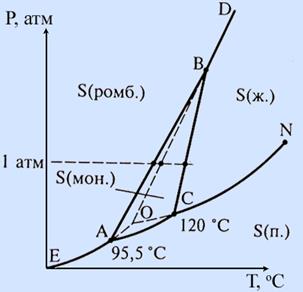
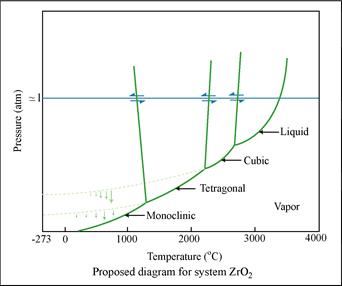
Рис. 5.11. Фазова діаграма сірки. Енантіотропні перетворення.	Рис. 5.12 Фазова діаграма ZrO2. Монотропні перетворення.

Випадок 2. Рис. 5.10 б. Істотна монотропія. Поверхні Гіббс-потенціалів поліморфних модифікацій S₁ і S₂ не перехрещуються. Нема зворотного переходу між твердими фазами. Лише односторонній S₁ ® S₂. Поверхня термодинамічного потенціалу рідини перехрещує поверхні для твердих фаз. Отже, перетворення S₁ « L і S₂ « L зворотні. Приклад – рис. 5.12.

Випадок 3. Рис. 5.10 в. Неістотна монотропія. Поверхні термодинамічних потенціалів твердих фаз перехрещуються, але вище температури плавлення. Тоді випадок тотожній істотній монотропії, адже тверде тіло не можна перегріти вище температури плавлення. Якщо змінити тиск таким чином, щоб точка М змістилася в бік нижчих температур і стала нижче за температуру плавлення, випадок стає тотожнім енантіотропії. При цьому на діаграмі стану має з’явитися відповідна точка, як показано на рис. 5.13.

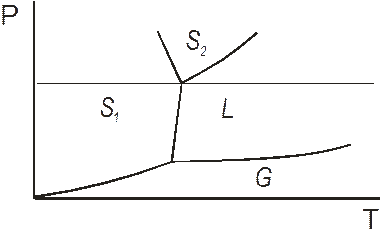
Рис. 5.13. Перехід від монотропії до енантіотропії для СО₂

Ви побачили різницю між компонентом (сполукою) і твердою фазою. Сполука (компонент) можуть існувати в різних твердих фазах. Одна сполука – декілька твердих фаз.