Це рівняння є аналітичним виразом першого закону термодинаміки.

Енергію системи можна збільшити здійснивши над нею роботу або передавши їй якусь кількість теплоти. Енергію системи можна зменшити, якщо робота виконується самою системою або від системи відводиться тепло.

Для нескінченно малих приростів

dU = dq – dA. (2.4)

Частинні диференціали dq та dA підкреслюють, що теплота і робота залежать від шляху процесу, на відміну від їх різниці. Рівняння (2.3) та (2.4) універсальні і справедливі для любих процесів (зворотних, незворотних) і любих агрегатних станів.

Таким чином, теплота і робота – еквівалентні способи зміни внутрішньої енергії. Система подібна до банку: вона приймає депозити у вигляді теплоти або роботи, і зберігає їх у вигляді внутрішньої енергії.

Перший закон, відтак, може бути записаний у вигляді

dU = dq – рdv. (2.5)

Величина А (2.4) є сумою робіт, які виконує система проти всіх зовнішніх сил (тиск, електричне поле і т.і.), тому

dА = рdv + dA₁, (2.6)

де dA₁ – корисна робота, або робота проти всіх зовнішніх сил за виключенням тиску. В більшості термодинамічних розрахунків враховують лише зовнішній тиск на систему, тому dA₁ = 0 і справедливе рівняння (2.5).

Розглянемо застосування рівняння (2.5) до окремих випадків:

1. v = const., dv = 0. Ізохорний процес. Тоді

dq_v = dU_v, або q_v = DU_v. (2.7)

Тут q_v не залежить від шляху процесу, і вся поглинена системою теплота іде на приріст внутрішньої енергії. Отже, теплота при сталому об’ємі є функцією стану.

2. р = const. Ізобарний процес. Тоді

dq_р = dU_p + d(pv) = d(U + pv)_p = dH_р, або q_р = DН_р (2.8)

де U + pv = Н. Це нова однозначна функція стану системи, яка називається ентальпія (в старих підручниках – тепловміст). В даному випадку q_р також не залежить від шляху процесу, а визначається початковим і кінцевим станами системи, отже є функцією стану. За умов постійного тиску вся поглинута системою теплота йде на збільшення ентальпії.

Ентальпія є дуже важливою функцією в термодинаміці металургійних процесів, адже більшість їх проводиться при сталому тиску, оскільки контролювати сталість об’єму набагато складніше.

3. dq = 0. Адіабатичний процес. Тоді

dU + pdv = 0, або pdv = -dU (2.9)

В цьому випадку робота, що виконується системою, виконується за рахунок зменшення її внутрішньої енергії.

Теплоємність. Важливою характеристикою матеріалів (особливо це стосується металів і сплавів) є теплоємність. Внутрішня енергія і ентальпія залежать від температури, рис. 2.2. Щоб визначити теплоємність при температурах Т₁ і Т₂, до кривої в точках 1 і 2 проведемо дотичні. Тангенс їх кута нахилу дорівнюватиме теплоємності при цих температурах.

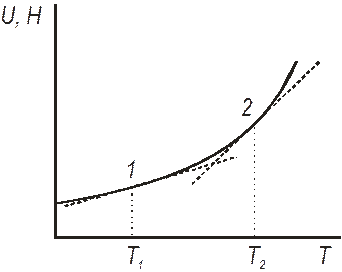
Рис.2.2. Визначення теплоємності при сталих об’ємі і тиску

В аналітичному вигляді

С_р = 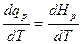. (2.10)

В цьому випадку говорять про теплоємність при сталому тиску. Для теоретичних розрахунків буває потрібна також теплоємність при сталому об’ємі, яка дорівнює

С_v = 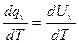. (2.11)

Отже, теплоємність – це кількість теплоти, необхідна для нагрівання тіла на 1 К, якщо при цьому не відбуваються фазові перетворення або хімічні реакції. Розділяють питому теплоємність і мольну теплоємність.Питома теплоємність – це кількість теплоти, яка витрачається при нагрівання 1 г речовини на 1 К.Мольна теплоємність – це кількість теплоти, яка витрачається при нагрівання 1 г-моль речовини на 1 К. В термодинаміці користуються мольною теплоємністю.

Експериментально теплоємність вимірюють в калориметрах в інтервалі температури. Оскільки вона залежить від температури (рис. 2.1), то отримують середню теплоємність, адже отримана системою теплота і, відповідно, зміна температури кінцеві

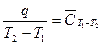(2.12)

Середня теплоємність відрізняється від істинної, для якої зміна теплоти і температури – нескінченно малі величини

С = 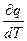. (2.13)

Для визначення істинної теплоємності треба істотно зменшити інтервал зміни температури DТ, однак це значно зменшує точність. Тому її розраховують виходячи з середніх теплоємностей і представляють у вигляді степеневих рядів для різних інтервалів температури. Наприклад, С_р = а + bt + dt^-2… .

Експериментально зазвичай вимірюють теплоємність при сталому тиску, хоча більш фундаментальною величиною є теплоємність при сталому об’ємі, адже внутрішня енергія – «фізичніше» поняття, ніж ентальпія. Саме С_v визначають при першопринципних розрахунках. Ці дві теплоємності пов’язані між собою простим співвідношенням:

С_р = С_v + aТ^3/2, (2.14)

де a – експериментальна константа, яку знаходять зі значення С_р для однієї температури.

Теплоємність C_v це сума теплоємності гратки і електронів і записується як

C_v = aТ³ + gТ. (2.15)

Коефіцієнт a пов’язаний з характеристичною температурою Дебая. g - також константа. При низьких температурах другий член стає їстотнішим. Електронна теплоємність пов’язана із спіновою магнітною сприятливістю і густиною електронів на рівні Фермі.