ГЕОМЕТРИЧЕСКОЕ И ЭНЕРГЕТИЧЕСКОЕ ПОНЯТИЯ ОСНОВНОГО УРАВНЕНИЯ ГИДРОСТАТИКИ
Преобразуем уравнение (2.2), записав значение 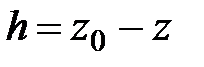 (рис. 2.6).
(рис. 2.6).
Для любой точки, например т. А,
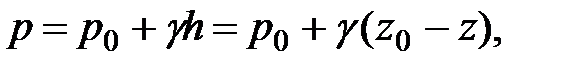
где z - координата т. A; 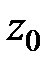 - координата свободной поверхности.
- координата свободной поверхности.
Получим
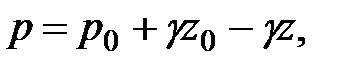
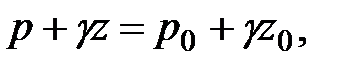
Разделим обе части полученного уравнения на величину 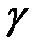 и сделаем перестановки слагаемых:
и сделаем перестановки слагаемых:
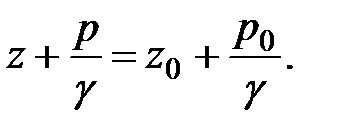 (2.3)
(2.3)
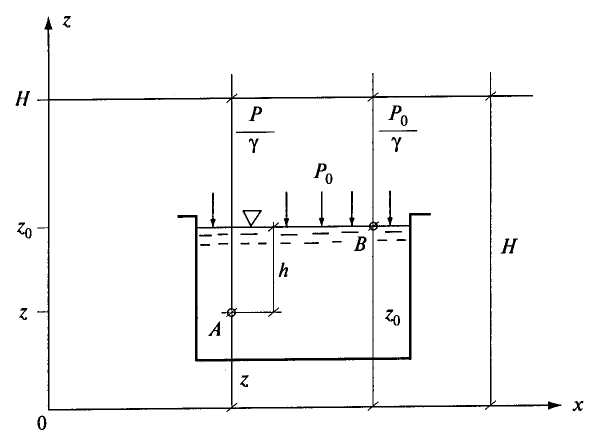
Рис. 2.6. Геометрическое пояснение основного уравнения гидростатики
Уравнение (2.3) также носит название основного уравнения гидростатики, но оно представлено в другой форме записи.
Каждый член этого уравнения имеет размерность метр: 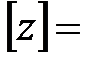 м;
м; 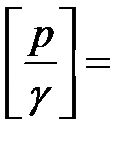 м. Значит, уравнение (2.3) можно представить как уравнение высот, в котором
м. Значит, уравнение (2.3) можно представить как уравнение высот, в котором
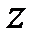 - высота положения точки (геометрический напор);
- высота положения точки (геометрический напор);
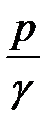 - высота, соответствующая давлению (напор).
- высота, соответствующая давлению (напор).
Так как 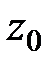 и
и 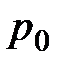 для рассматриваемого резервуара - величины конкретные, можно записать
для рассматриваемого резервуара - величины конкретные, можно записать
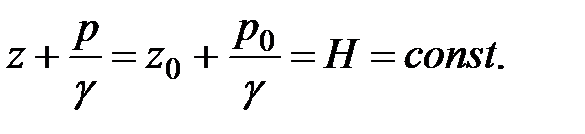 (2.4)
(2.4)
Величину Н называют гидростатическим (потенциальным) напором. Эта величина одинакова для любой точки жидкости, находящейся в рассматриваемом резервуаре с постоянными 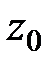 и
и 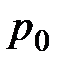 .
.
Плоскость xOz называют плоскостью сравнения или начальной плоскостью.
Но уравнение (2.3) 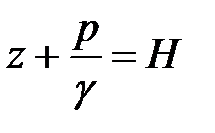 легко выразить в единицах энергии, для этого достаточно умножить каждый член уравнения на 1 Н (ньютон), тогда все слагаемые будут выражены в единицах энергии (Дж=Н
легко выразить в единицах энергии, для этого достаточно умножить каждый член уравнения на 1 Н (ньютон), тогда все слагаемые будут выражены в единицах энергии (Дж=Н  м). Значит, каждое слагаемое уравнения (2.3) представляет собой вид потенциальной энергии, так как жидкость находится в покое:
м). Значит, каждое слагаемое уравнения (2.3) представляет собой вид потенциальной энергии, так как жидкость находится в покое:
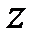 - удельная потенциальная энергия положения;
- удельная потенциальная энергия положения;
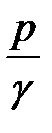 - удельная потенциальная энергия давления;
- удельная потенциальная энергия давления;
Н - полный запас удельной потенциальной энергии.
Слово «удельная» означает энергию, приходящуюся на единицу веса жидкости (на 1 Н). Следует отметить, что в гидравлике слово «напор» означает удельную энергию жидкости и может применяться наряду со словом «высота», так как имеет ту же размерность [м].
Дата добавления: 2016-02-27; просмотров: 732;
