СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКУЮ ПОВЕРХНОСТЬ
Пусть некоторая плоская поверхность площадью 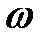 сложной геометрической, формы лежит в пределах координатной плоскости xOz, имеющей наклон к горизонту под углом
сложной геометрической, формы лежит в пределах координатной плоскости xOz, имеющей наклон к горизонту под углом 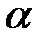 (рис. 2.12). Над поверхностью находится жидкость глубиной Н.
(рис. 2.12). Над поверхностью находится жидкость глубиной Н.
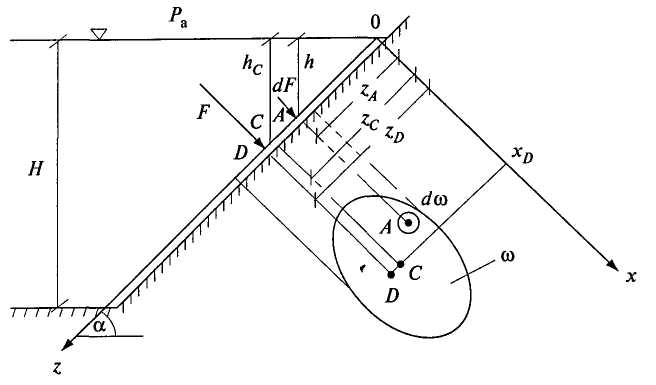
Рис. 2.12
Ось Ох лежит на линии пересечения координатной плоскости и свободной поверхности жидкости (т.е. ось Ох перпендикулярна плоскости чертежа). Определим результирующую силу избыточного давления жидкости на эту плоскую поверхность.
Для того чтобы видеть форму площадки 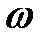 и иметь возможность наносить на нее нужные обозначения, развернем координатную плоскость xOz вокруг оси Oz и совместим с плоскостью чертежа.
и иметь возможность наносить на нее нужные обозначения, развернем координатную плоскость xOz вокруг оси Oz и совместим с плоскостью чертежа.
Выделим элементарную площадку 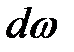 в пределах поверхности
в пределах поверхности 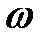 около некоторой т. А, находящейся на глубине h. Сила избыточного давления на эту элементарную площадку
около некоторой т. А, находящейся на глубине h. Сила избыточного давления на эту элементарную площадку 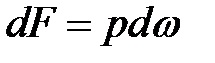 ,где
,где 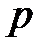 - среднее значение давления в пределах
- среднее значение давления в пределах 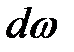 на глубине h,
на глубине h, 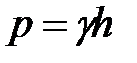 . Тогда
. Тогда 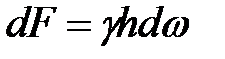 , а суммарное давление на всю поверхность
, а суммарное давление на всю поверхность 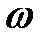 определится как
определится как
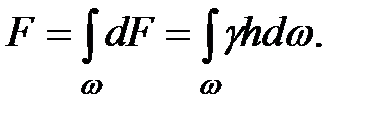
Выразим h через координату т. А по оси 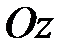 (z) и угол наклона поверхности (
(z) и угол наклона поверхности ( 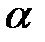 ):
):
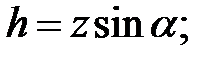
тогда
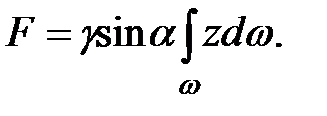
Произведение 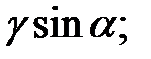 вынесено за знак интеграла как постоянная величина. Из теоретической механики известно, что
вынесено за знак интеграла как постоянная величина. Из теоретической механики известно, что 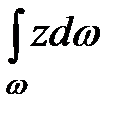 представляет собой статический момент площади
представляет собой статический момент площади 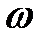 относительно оси Ох. Статический момент равен произведению площади
относительно оси Ох. Статический момент равен произведению площади 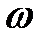 на плечо, равное расстоянию от оси Ох до центра тяжести поверхности. На рис. 2.12 центр тяжести
на плечо, равное расстоянию от оси Ох до центра тяжести поверхности. На рис. 2.12 центр тяжести 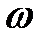 обозначен т.С.
обозначен т.С.
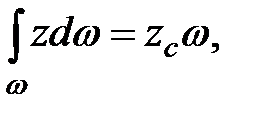
тогда 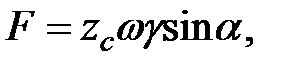
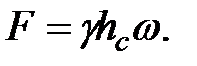 (2.9)
(2.9)
Но 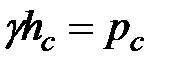 - гидростатическое давление в центре тяжести рассматриваемой поверхности (hc - глубина погружения центра тяжести площадки под уровень свободной поверхности).
- гидростатическое давление в центре тяжести рассматриваемой поверхности (hc - глубина погружения центра тяжести площадки под уровень свободной поверхности).
Уравнение (2.9) показывает, что результирующая сила давления жидкости на любую плоскую площадку равна произведению гидростатического давления в центре тяжести этой площадки на ее площадь.
Если требуется определить силу абсолютного давления на плоскую поверхность, то формула для F будет иметь следующий вид:
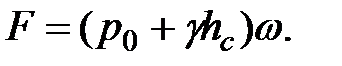 (2.10)
(2.10)
ЦЕНТР ДАВЛЕНИЯ
Точка приложения результирующей силы давления жидкости на любую поверхность называется центром давления.
Применительно к рис. 2.12 центром давления является т. D. Определим координаты центра давления (xD; zD) для любой плоской поверхности.
Из теоретической механики известно, что момент равнодействующей силы относительно произвольной оси равен сумме моментов составляющих сил относительно той же оси. За ось в нашем случае примем ось Ох (см. рис. 2.12), тогда
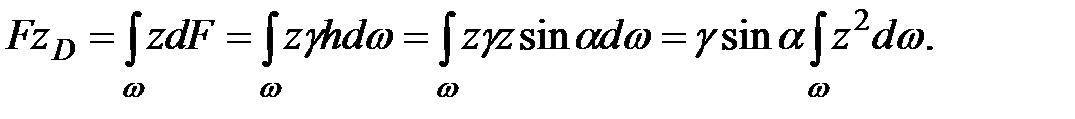
Известно также, что 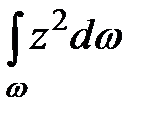 является моментом инерции площади
является моментом инерции площади 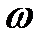 относительно оси Ox
относительно оси Ox 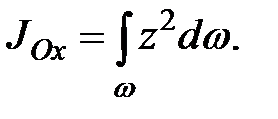
В результате получаем
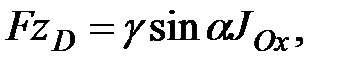
откуда
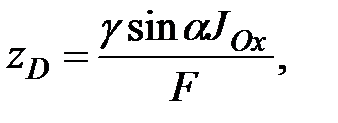
Подставим в это выражение формулу (2.9) для F и геометрическое соотношение 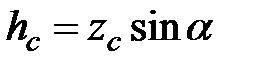 :
:
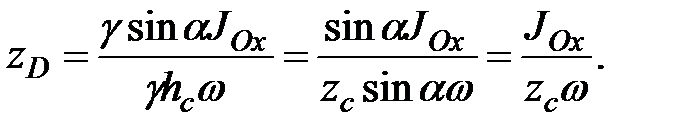
Перенесем ось момента инерции в центр тяжести площадки 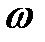 . Обозначим момент инерции относительно оси, параллельной оси Ох и проходящей через т.С, через
. Обозначим момент инерции относительно оси, параллельной оси Ох и проходящей через т.С, через 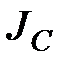 . Моменты инерции относительно параллельных осей связаны соотношением
. Моменты инерции относительно параллельных осей связаны соотношением
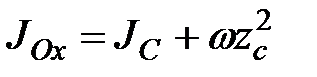 ;
;
тогда 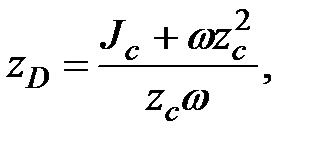 и окончательно получим
и окончательно получим
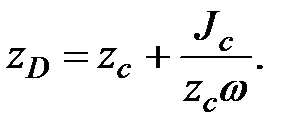 (2.11)
(2.11)
Формула показывает, что центр давления расположен всегда ниже центра тяжести площадки, за исключением случая, если площадка горизонтальна и центр давления совпадает с центром тяжести. Для простых геометрических фигур моменты инерции относительно оси, проходящей через центр тяжести и параллельной оси Ох (рис. 2.12), определяются по следующим формулам:
для прямоугольника
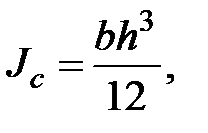 (2.12)
(2.12)
где сторона основания параллельна Ох;
для равнобедренного треугольника
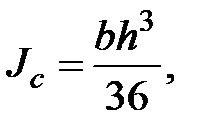 (2.13)
(2.13)
где сторона основания параллельна Ох;
для круга
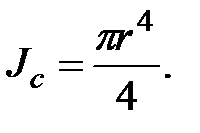 (2.14)
(2.14)
Координата 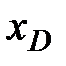 для плоских поверхностей строительных конструкций чаще всего определяется по координате расположения оси симметрии геометрической фигуры, ограничивающей плоскую поверхность. Так как такие фигуры (круг, квадрат, прямоугольник, треугольник) имеют ось симметрии, параллельную координатной оси Oz, местоположение оси симметрии и определяет координату xD. Например, для прямоугольной плиты (рис. 2.13), определение координаты xD ясно из чертежа.
для плоских поверхностей строительных конструкций чаще всего определяется по координате расположения оси симметрии геометрической фигуры, ограничивающей плоскую поверхность. Так как такие фигуры (круг, квадрат, прямоугольник, треугольник) имеют ось симметрии, параллельную координатной оси Oz, местоположение оси симметрии и определяет координату xD. Например, для прямоугольной плиты (рис. 2.13), определение координаты xD ясно из чертежа.
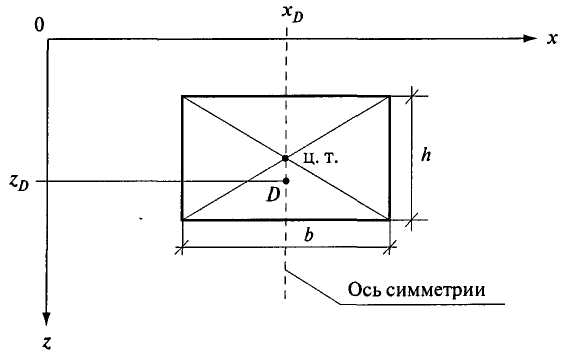
Рис. 2.13. Схема расположения центра давления для прямоугольной поверхности
Гидростатический парадокс.Рассмотрим силу давления жидкости на дно сосудов, изображенных на рис. 2.14.
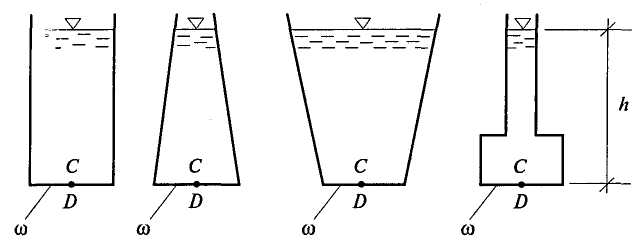
Рис. 2.14. Сила давления на дно сосудов различных форм
Несмотря на разную форму объемов сосудов, изображенных на этом рисунке, сила давления на дно каждого из них будет одинакова, хотя вес налитой в каждый объем жидкости будет различен. Действительно, 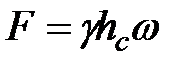 , но
, но 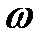 и hc для всех сосудов одинаковы.
и hc для всех сосудов одинаковы.
Дата добавления: 2016-02-27; просмотров: 1925;
