Глава 1. ЖИДКОСТИ И ИХ ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА
Жидкости.В природе различают четыре вида состояния вещества: твердое, жидкое, газообразное и плазменное. Основное отличие жидкостей от твердых тел заключается в их текучести, т.е. способности легко принимать форму сосуда, в который жидкость поместили, при этом объем жидкости не изменяется. Газ тоже обладает текучестью, но при этом занимает любой предоставленный ему объем. В сосудах жидкость образует свободную поверхность, а газ аналогичной поверхностью не обладает. Однако с точки зрения механики и жидкость, и газ подчиняются одним и тем же закономерностям в случае, если сжимаемостью газа можно пренебречь. Поэтому в гидравлике под термином «жидкость» понимаются и собственно жидкости (которые часто называют капельными жидкостями), и газы (газообразные жидкости).
Основные свойства жидкости (при рассмотрении задач механики жидкости) - это плотность, способность изменять свой объем при нагревании (охлаждении) и изменениях давления, вязкость жидкости. Рассмотрим каждое из свойств жидкости подробнее.
Плотность жидкости.Плотностью жидкости 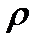 называется ее масса, заключенная в единице объема:
называется ее масса, заключенная в единице объема:
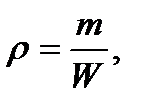 (1.1)
(1.1)
где  - масса жидкости;
- масса жидкости; 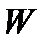 - объем жидкости.
- объем жидкости.
Единица измерения плотности - кг/м3.
Так как вода является наиболее распространенной в природе жидкостью, в качестве примера количественного значения параметра, определяющего то или иное свойство жидкости, будем приводить значение рассматриваемого параметра для воды. Плотность воды при 4°С 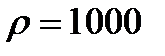 кг/м3. Плотность жидкости уменьшается при увеличении температуры. Однако для воды эта закономерность справедлива только с 4 °С, в чем проявляется одно из аномальных свойств воды.
кг/м3. Плотность жидкости уменьшается при увеличении температуры. Однако для воды эта закономерность справедлива только с 4 °С, в чем проявляется одно из аномальных свойств воды.
Удельный вес.Удельный вес 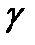 - это вес жидкости, приходящийся на единицу объема:
- это вес жидкости, приходящийся на единицу объема:
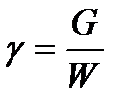 (1.2)
(1.2)
где 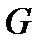 - вес жидкости в объеме
- вес жидкости в объеме 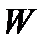 .
.
Единица измерения удельного веса - Н/м3. Удельный вес воды при температуре 4°С  Н/м3.
Н/м3.
Плотность и удельный вес связаны между собой соотношением
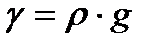 (1.3)
(1.3)
где 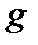 - ускорение свободного падения.
- ускорение свободного падения.
Температурное расширение.Это свойство жидкости характеризуется изменением объема при изменении температуры, которое определяется температурным коэффициентом объемного расширения жидкости 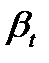 :
:
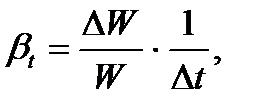 (1.4)
(1.4)
где 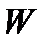 - начальный объем жидкости при начальной температуре;
- начальный объем жидкости при начальной температуре; 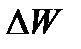 - изменение объема после уменьшения или увеличения температуры;
- изменение объема после уменьшения или увеличения температуры; 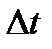 - изменение температуры.
- изменение температуры.
Единица измерения 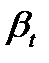 - град-1, для воды при
- град-1, для воды при  °С
°С 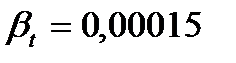 1/°С.
1/°С.
Сжимаемость.Это свойство жидкости менять свой объем при изменении давления, которое характеризуется коэффициентом объемного сжатия 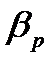 :
:
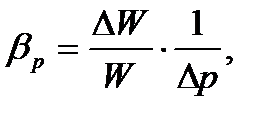 (1.5)
(1.5)
где 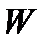 - начальный объем жидкости;
- начальный объем жидкости; 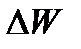 -изменение объема после изменения давления;
-изменение объема после изменения давления; 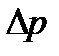 - изменение давления.
- изменение давления.
Единица измерения 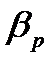 - Па-1.
- Па-1.
Коэффициент объемного сжатия капельных жидкостей мало меняется в зависимости от давления и температуры. Для воды 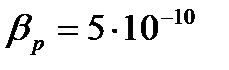 Па-1.
Па-1.
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости 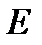 и определяется по формуле
и определяется по формуле
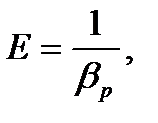 (1.6)
(1.6)
Для воды 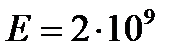 Па.
Па.
Вязкость жидкости- свойство жидкостей оказывать сопротивление сдвигу. Это свойство проявляется только при движении жидкостей. Вязкость характеризует степень текучести жидкости. Наряду с легко подвижными жидкостями (вода, спирт, воздух и др.) существуют очень вязкие жидкости (глицерин, машинные масла и др.).
Вязкость жидкости характеризуется динамической вязкостью 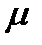 .
.
И. Ньютон выдвинул гипотезу о силе трения F, возникающей между двумя слоями жидкости на поверхности их раздела площадью 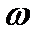 , согласно которой сила внутреннего трения в жидкости не зависит от давления, прямо пропорциональна площади соприкосновения слоев
, согласно которой сила внутреннего трения в жидкости не зависит от давления, прямо пропорциональна площади соприкосновения слоев 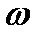 и быстроте изменения скорости в направлении, перпендикулярном направлению движения слоев, и зависит от рода жидкости.
и быстроте изменения скорости в направлении, перпендикулярном направлению движения слоев, и зависит от рода жидкости.
Пусть жидкость течет по плоскому дну параллельными ему слоями (рис. 1.1).
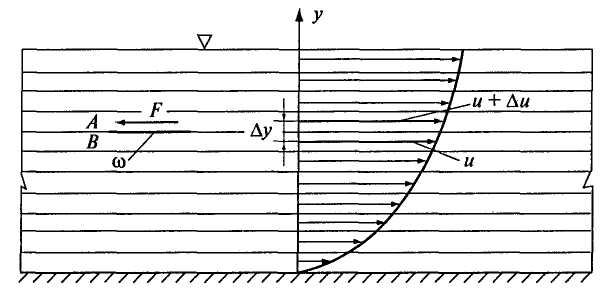
Рис.1.1
Вследствие тормозящего влияния дна слои жидкости будут двигаться с разными скоростями. На рис. 1.1 скорости слоев показаны стрелками. Рассмотрим два слоя жидкости, середины которых расположены на расстоянии 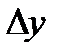 друг от друга. Слой А движется со скоростью
друг от друга. Слой А движется со скоростью 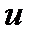 , а слой В - со скоростью
, а слой В - со скоростью 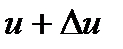 .
.
На площадке 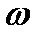 вследствие вязкости возникает сила сопротивления F. Согласно гипотезе Ньютона эта сила
вследствие вязкости возникает сила сопротивления F. Согласно гипотезе Ньютона эта сила
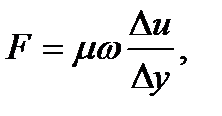 (1.7)
(1.7)
коэффициент пропорциональности 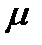 в этой формуле и является динамической вязкостью, отношение
в этой формуле и является динамической вязкостью, отношение 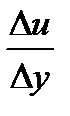 называется градиентом скорости.
называется градиентом скорости.
Таким образом, динамическая вязкость является силой трения, приходящейся на единицу площади соприкосновения слоев жидкости при градиенте скорости, равном единице. Размерность 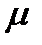 - Па
- Па  с.
с.
Гипотеза И. Ньютона, представленная в формуле (1.7), экспериментально подтверждена и математически оформлена в дифференциальном виде
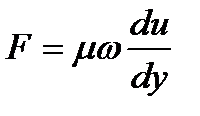 (1.8)
(1.8)
основоположником гидравлической теории смазки Н.П. Петровым и в настоящее время носит название закона внутреннего трения Ньютона.
В гидравлических расчетах часто удобнее пользоваться другой величиной, характеризующей вязкость жидкости, - 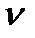 :
:
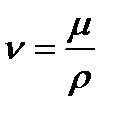 (1.9)
(1.9)
Эта величина называется кинематической вязкостью. Размерность 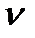 - м2/с.
- м2/с.
Название «кинематическая вязкость» не несет особого физического смысла, так как название было предложено потому, что размерность 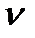 похожа на размерность скорости.
похожа на размерность скорости.
Вязкость жидкости зависит как от температуры, так и от давления. Кинематическая вязкость капельных жидкостей уменьшается с увеличением температуры, а вот вязкость газов, наоборот, возрастает с увеличением температуры. Кинематическая вязкость жидкостей при давлениях, встречающихся в большинстве случаев на практике, мало зависит от давления, а вязкость газов с возрастанием давления уменьшается.
Вязкость жидкости измеряют с помощью вискозиметров различных конструкций.
Жидкости, для которых справедлив закон внутреннего трения Ньютона (1.8), называют ньютоновскими. Существуют жидкости, которые не подчиняются закономерности (1.8), к ним относятся растворы полимеров, гидросмеси из цемента, глины, мела и др. Такие жидкости относятся к неньютоновским.
Пример 1.1
Определите массу бензина, заполняющего цилиндрический резервуар диаметром 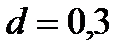 м и высотой
м и высотой 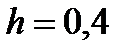 м при температуре 20°С (
м при температуре 20°С ( 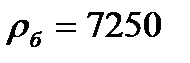 кг/м3).
кг/м3).
Ответ: 204,9кг.
Пример 1.2
Определите количественные изменения давления в воде, находящейся в герметически замкнутом резурвуаре, при изменении температуры от 10 до 20°С, если считать материал резервуара абсолютно жестким.
Если бы резервуар не был закрыт герметически, изменение объема можно было бы найти из формулы (1.4) 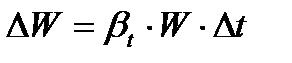 . Тогда новый объем
. Тогда новый объем 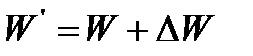 , но объем неизменен. Значит, должно измениться внешнее давление на поверхности воды, а значит, и давление в каждой ее точке не величину
, но объем неизменен. Значит, должно измениться внешнее давление на поверхности воды, а значит, и давление в каждой ее точке не величину 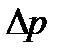 , которую определим из формулы (1.5):
, которую определим из формулы (1.5):
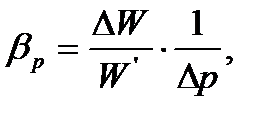
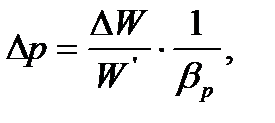
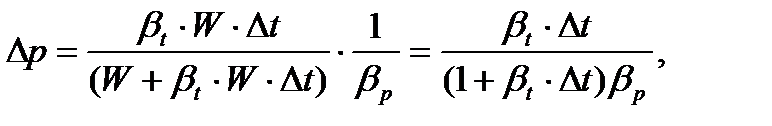
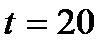 °С,
°С, 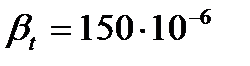 1/°С,
1/°С,
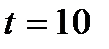 °С,
°С, 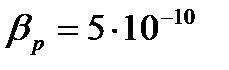 Па-1,
Па-1,
Тогда
 Па.
Па.
Дата добавления: 2016-02-27; просмотров: 709;
