КОЭФФИЦИЕНТА И КОЭФФИЦИЕНТА ШЕЗИ С
При ламинарном движении жидкости в трубах 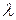 определяют по теоретической формуле
определяют по теоретической формуле  .
.
Для турбулентного режима движения было предложено достаточно большое число формул для нахождения 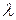 . Предлагаемые формулы были чисто эмпирическими, основанными на результатах экспериментов, а также полученными в результате анализа размерности и теории подобия при исследовании турбулентного режима. В формулах при определении коэффициента обычно использовалась эквивалентная шероховатость
. Предлагаемые формулы были чисто эмпирическими, основанными на результатах экспериментов, а также полученными в результате анализа размерности и теории подобия при исследовании турбулентного режима. В формулах при определении коэффициента обычно использовалась эквивалентная шероховатость  . В табл. 4.1 приведены значения
. В табл. 4.1 приведены значения  для труб, изготовленных из различных материалов.
для труб, изготовленных из различных материалов.
Таблица 4.1 - Значения эквивалентной шероховатости 
и коэффициента шероховатости n для напорных труб и водоводов
| Характеристика поверхности труб | 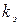 , мм , мм
| n |
| 1. Цельнотянутые трубы: | ||
| технические гладкие из латуни, меди и свинца | 0,002  0,01 0,01
| - |
| пластмассовые (полиэтилен, винипласт) | 0,0015  0,005 0,005
| - |
| новые стальные | 0,02  0,05 0,05
| - |
| стальные, после нескольких лет эксплуатации, битумизированные, умеренно корродированные | 0,15  0,3 0,3
| 0,013 |
| стальные водопроводные, находящиеся в эксплуатации | 1,0  1,2 1,2
| 0,014 |
| 2. Сварные стальные трубы: | ||
| новые и в хорошем состоянии | 0,04  0,1 0,1
| 0,01 |
| после нескольких лет эксплуатации | 0,1  0,2 0,2
| 0,012 |
| новые битумизированные |  0,05 0,05
| - |
| находящиеся в продолжительной эксплуатации | 0,1  1,5 1,5
| - |
| 3. Чугунные трубы: | ||
| новые | 0,2  0,5 0,5
| 0,013  0,014 0,014
|
| новые битумизированные | 0,1  0,15 0,15
| 0,011  0,012 0,012
|
| асфальтированные | 0,12  0,3 0,3
| - |
| водопроводные, бывшие в эксплуатации | 1  1,4 1,4
| - |
| со значительными отложениями | 2,0  4,0 4,0
| - |
| сильно корродированные | До 3,0 | - |
| 4. Асбоцементные трубы | 0,6 | 0,0086 |
| 5. Керамические трубы | 1,35 | 0,013 |
Для всех областей турбулентного движения известны универсальные формулы Колбрука и А. Альтшуля для определения 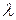 .
.
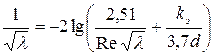 . (4.94)
. (4.94)
Формула А. Альтшуля:
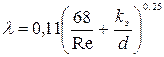 . (4.95)
. (4.95)
В области гладкого сопротивления (гидравлически гладкие трубы)  и
и 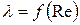 . В этой области сопротивления числа Рейнольдса лежат в следующих пределах:
. В этой области сопротивления числа Рейнольдса лежат в следующих пределах:
 . (4.96)
. (4.96)
Формулы (4.94) и (4.95) преобразуются следующим образом:
 (4.97)
(4.97)
 (4.98)
(4.98)
Для гладких труб применяется формула Блазиуса
 . (4.99)
. (4.99)
Следует отметить что зависимости (4.98) и (4.99) практически совпадают.
При определении 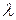 нашла широкое применение формула П. Конакова
нашла широкое применение формула П. Конакова
 . (4.l00)
. (4.l00)
В области доквадратичного (переходного сопротивления)  . Эта область находится в пределах
. Эта область находится в пределах
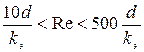 . (4.101)
. (4.101)
Коэффициент гидравлического трения находится, как правило, по универсальным формулам (4.94) и (4.95).
Область квадратичного сопротивления, когда  и
и  , лежит в следующих пределах:
, лежит в следующих пределах:
 . (4.102)
. (4.102)
Формулы (4.97) и (4.98) для определения коэффициента гидравлического трения имеют следующий вид:
 ; (4.103)
; (4.103)
 . (4.104)
. (4.104)
Формула (4.103) соответствует формуле Шифринсона (4.104).
Для стальных и чугунных труб, находящихся в эксплуатации, коэффициент 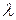 , может быть вычислен по формуле Ф. Шевелева при
, может быть вычислен по формуле Ф. Шевелева при 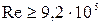 :
:
 (4.105)
(4.105)
Следует отметить, что в результате эксплуатации шероховатость стенок труб увеличивается со временем.
Для полиэтиленовых труб коэффициент 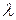 , может быть вычислен по формуле
, может быть вычислен по формуле
 . (4.106)
. (4.106)
В случае применения асбоцементных труб
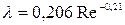 . (4.107)
. (4.107)
Как уже отмечалось ранее, коэффициент Шези связан с коэффициентом гидравлического трения 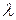 (4.47):
(4.47):
 , или
, или  .
.
Коэффициент Шези зависит от относительной шероховатости стенок трубы или открытых русел в квадратичной области, а в переходной области сопротивления на С влияет скорость движения жидкости, а следовательно, число Re. Поэтому формула Шези применяется, как правило, в случае квадратичного сопротивления. Коэффициент Шези является размерной величиной (м1/2/с). В результате исследований, проведенных многими учеными, были получены достаточно простые зависимости для определения коэффициента С Шези.
В случае круглых и прямоугольных труб С можно находить по формуле (4.47), зная коэффициент гидравлического трения 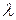 .
.
Приводим некоторые формулы для вычисления коэффициента С.
Формула Н. Павловского
 , (4.108)
, (4.108)
где  - коэффициент шероховатости стенок русла; у - показатель степени при
- коэффициент шероховатости стенок русла; у - показатель степени при  м;
м;
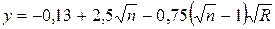 . (4.109)
. (4.109)
Более простые зависимости:
 при
при  м; (4.110)
м; (4.110)
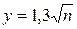 при
при  м.
м.
Известны частные случаи формулы Н. Павловского:
формула Маннинга
 ; (4.111)
; (4.111)
формула Форгеймера
 . (4.112)
. (4.112)
Значения коэффициента шероховатости труб  представлены в табл. 4.1.
представлены в табл. 4.1.
Дата добавления: 2016-02-27; просмотров: 1652;
