КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ В ТУРБУЛЕНТНОМ ПОТОКЕ
Касательные напряжения, возникающие в турбулентном потоке, по своей физической природе существенно отличаются от касательных напряжений в ламинарном потоке. В результате интенсивного перемешивания частиц происходит массообмен частицами в поперечном направлении между отдельными слоями, что приводит к обмену количеством движения.
Определим касательные напряжения, возникающие в турбулентном потоке вдоль оси х, в котором имеются пульсации скоростей, приняв струйчатую модель движения (рис. 4.9). Выделим в потоке жидкости два слоя: первый слой - движения со скоростью 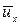 , второй - с большей скоростью на величину
, второй - с большей скоростью на величину 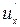 , т.е.
, т.е. 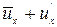 .
.

Рис. 4.9. К определению касательных турбулентных напряжений
За счет поперечной пульсационной скорости  происходит обмен массами между слоями через некоторую площадь
происходит обмен массами между слоями через некоторую площадь  . За время dt через площадь
. За время dt через площадь  от слоя 1 к слою 2 пройдет следующая малая масса жидкости:
от слоя 1 к слою 2 пройдет следующая малая масса жидкости:
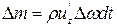 . (4.73)
. (4.73)
Эта масса жидкости за счет продольной пульсации 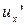 передаст слою 2 следующее количество движения:
передаст слою 2 следующее количество движения:
 . (4.74)
. (4.74)
В результате передачи количества движения в слое 2 возникает импульс силы
 , (4.75)
, (4.75)
где  - воображаемая сила трения, вектор которой параллелен направлению движения слоев.
- воображаемая сила трения, вектор которой параллелен направлению движения слоев.
Используя теорему количества движения (изменение количества движения равно импульсу движущих сил), получим
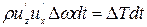 (4.76)
(4.76)
или
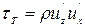 (4.77)
(4.77)
где 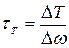 - касательные напряжения в турбулентном потоке.
- касательные напряжения в турбулентном потоке.
Уравнение выражает мгновенное значение касательных напряжений, обусловленных пульсацией скорости при турбулентном движении.
Осредненные касательные напряжения турбулентного трения представляются в виде
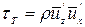 , (4.78)
, (4.78)
где  ,
, 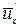 - осредненные пульсационные составляющие.
- осредненные пульсационные составляющие.
В турбулентном потоке имеют место вязкостные напряжения, связанные с силами внутреннего трения в результате сцепления частиц в потоке, а также со стенками русла. Полные касательные напряжения в результате турбулентного перемешивания  и вязкостного трения
и вязкостного трения 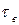
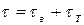 (4.79)
(4.79)
или
 , (4.80)
, (4.80)
где  - динамическая вязкость.
- динамическая вязкость.
Согласно теории Прандтля пульсационные скорости 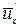 и
и  достаточно близки (
достаточно близки (  ), а пульсационная осредненная составляющая
), а пульсационная осредненная составляющая
 ,
,
где l - значение перемещения частиц или длина пути смешивания.
Тогда, подставив (4.81) в (4.78), получим формулу турбулентных касательных напряжений:
 . (4.82)
. (4.82)
Согласно гипотезе Прандтля величина 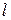 принимается пропорциональной расстоянию в рассматриваемой точке z от стенки русла потока, т.е.
принимается пропорциональной расстоянию в рассматриваемой точке z от стенки русла потока, т.е.
 , (4.83)
, (4.83)
где a - некоторое постоянное число.
По Прандтлю следует, что по мере удаления от стенки значение перемещений частиц жидкости 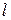 в поперечном направлении увеличивается. Число а обычно называют универсальной постоянной Прандтля.
в поперечном направлении увеличивается. Число а обычно называют универсальной постоянной Прандтля.
В результате исследований турбулентного потока в трубах, связанных с распределением скоростей, Никурадзе получил a=0,4.
По предложению Буссинеска турбулентные касательные напряжения по аналогии с законом Ньютона можно представить в виде
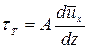 , (4.84)
, (4.84)
где А - коэффициент турбулентного перемешивания, связанный с переносом количества движения в результате интенсивности турбулентного перемешивания.
Учитывая равенства для 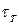 (4.82) и (4.84),
(4.82) и (4.84),
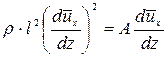 , (4.85)
, (4.85)
получим
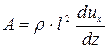 . (4.86)
. (4.86)
По аналогии с законом трения Ньютона обозначим  , где
, где 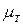 - динамическая виртуальная (турбулентная) вязкость.
- динамическая виртуальная (турбулентная) вязкость.
Выражение (4.82) может быть представлено в следующем виде:
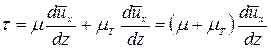 .
.
При сильно турбулизированном потоке вязкостные напряжения пренебрежительно малы, и тогда касательные напряжения
 .
.
Дата добавления: 2016-02-27; просмотров: 1122;
