УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ЭЛЕМЕНТАРНОЙ СТРУЙКИ ИДЕАЛЬНОЙ ЖИДКОСТИ
Выделим в потоке при установившемся движении идеальной жидкости, находящейся в поле сил тяжести, элементарную струйку (рис. 3.7). Рассмотрим часть струйки, заключенную между сечениями 1-1 и 2-2, и проведем горизонтальную плоскость 0-0, называемую плоскостью сравнения. Площадь первого живого сечения струйки 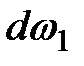 , скорость струйки
, скорость струйки 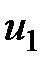 , давление
, давление 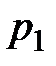 ,
, 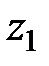 - высота расположения центра живого сечения над плоскостью сравнения 0-0.
- высота расположения центра живого сечения над плоскостью сравнения 0-0.
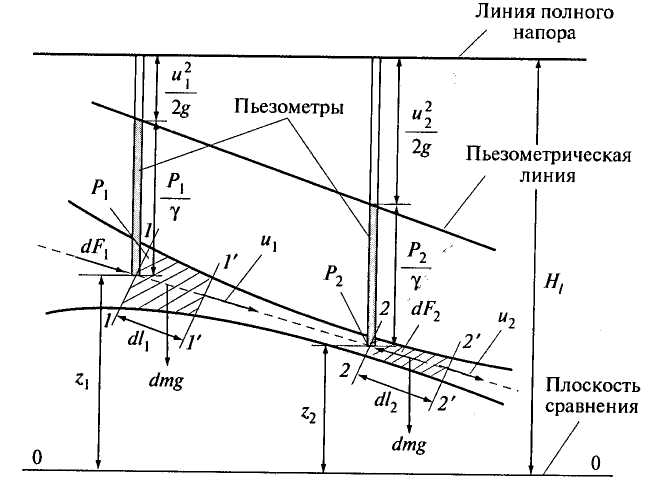
Рис. 3.7. К выводу уравнения Бернулли для струйки идеальной жидкости
Во втором сечении площадь 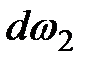 , скорость
, скорость 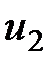 , давление
, давление 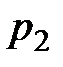 , высота положения сечения
, высота положения сечения 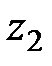 .
.
Рассмотрим элементарное перемещение за малый промежуток времени 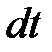 объема струйки из положения 1-1 и 2-2 в положение 1'-1' и 2'-2'. Перемещение первого сечения
объема струйки из положения 1-1 и 2-2 в положение 1'-1' и 2'-2'. Перемещение первого сечения 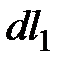 - расстояние между положениями 1-1', второго
- расстояние между положениями 1-1', второго 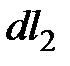 - между 2-2'. Выразим перемещения через скорости в сечениях:
- между 2-2'. Выразим перемещения через скорости в сечениях:
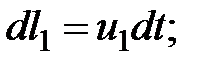
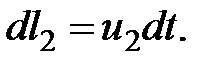 (3.27)
(3.27)
Используем для вывода уравнения Бернулли теорему о кинетической энергии. Для твердого тела она формулируется следующим образом: приращение кинетической энергии тела на любом пути его движения равно сумме работ, совершаемых на этом пути внешними силами, приложенными к телу.
Это допустимо применить к элементарной струйке, так как идеальная жидкость несжимаема, плотность жидкости 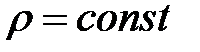 .
.
Теорему кинетической энергии можно представить в виде следующего уравнения:
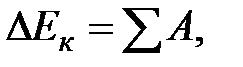 (3.28)
(3.28)
где 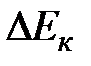 - приращение кинетической энергии;
- приращение кинетической энергии; 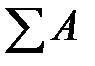 - сумма работ внешних сил.
- сумма работ внешних сил.
Силами, действующими на выделяемый объем жидкости, являются силы давления, приложенные нормально к живым сечениям участка струйки, и силы тяжести.
Силы гидродинамического давления, действующие нормально к поверхности участка струйки, нормальны линиям тока (оси движения). Работа этих сил при перемещении струйки равна нулю.
Силы гидростатического давления в сечениях 1-1 и 2-2 равны
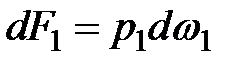 и
и 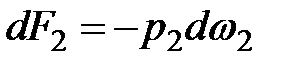 (3.29)
(3.29)
Направление силы 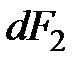 прямо противоположно направлению перемещения, поэтому перед силой
прямо противоположно направлению перемещения, поэтому перед силой 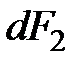 ставится знак минус.
ставится знак минус.
Работа силы давления на перемещение сечения 1-1 на расстояние 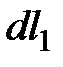 равна
равна
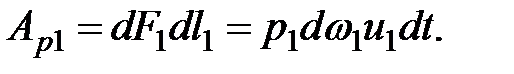 (3.30)
(3.30)
Работа силы давления для второго сечения 2-2
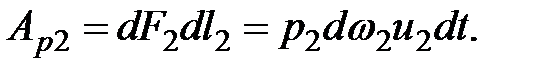 (3.31)
(3.31)
Работа сил давления на рассматриваемый объем части струйки
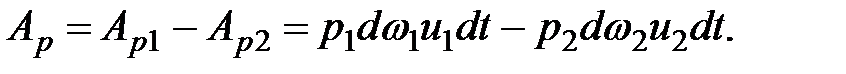 (3.32)
(3.32)
Произведения 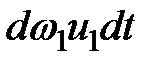 и
и 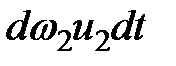 - объемы жидкости, проходящие через сечения 1-1 и 2-2. Умножив и разделив объемы на плотность жидкости, получим относительные элементарные массы, которые будут равны согласно уравнению неразрывности
- объемы жидкости, проходящие через сечения 1-1 и 2-2. Умножив и разделив объемы на плотность жидкости, получим относительные элементарные массы, которые будут равны согласно уравнению неразрывности
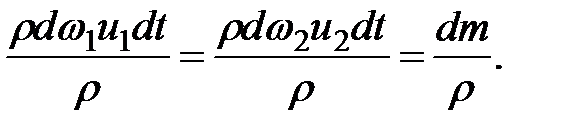 (3.33)
(3.33)
Отсюда работа сил давления
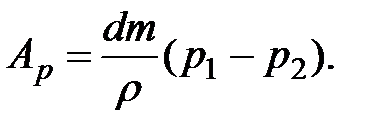 (3.34)
(3.34)
Работа силы тяжести равна изменению потенциальной энергии положения выбранного участка струйки. Из потенциальной энергии объема жидкости, заключенного между сечениями 1-1 и 2-2, нужно вычесть энергию объема между сечениями 1'-1' и 2'-2'. Потенциальные энергии участков 1-2 и 1'-2'' составят:
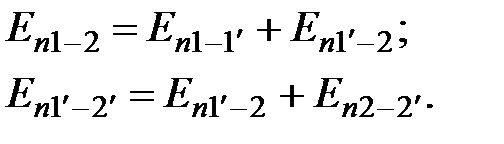 (3.35)
(3.35)
Работа сил тяжести равна разности потенциальных энергий:
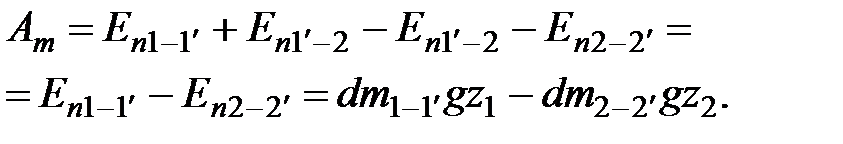 (3.36)
(3.36)
Масса жидкости в 1-1' и 2-2'
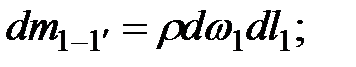
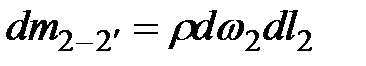
Массы жидкости находятся на высоте 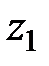 , и
, и 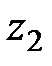 относительно плоскости сравнения. Работа сил тяжести
относительно плоскости сравнения. Работа сил тяжести
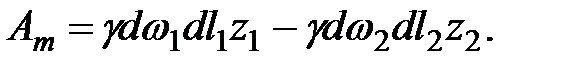 (3.37)
(3.37)
Массы жидкости, проходящие через сечения 1-1 и 2-2, равны
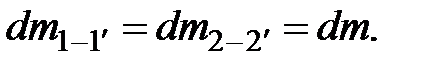
Работа сил тяжести
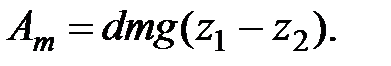 (3.38)
(3.38)
Сумма работ сил давления и тяжести согласно (3.34) и (3.38)
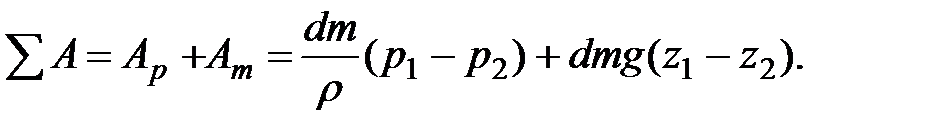 (3.39)
(3.39)
Приращение кинетической энергии равно изменению энергии массы объема жидкости 1'-2' и объема 1-2. Вычитаем из кинетической энергии массы объема 1'-2' энергию первоначального объема 1-2:
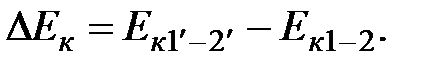
В энергии массы объемов жидкости входит энергия средней части объема 1'-2:
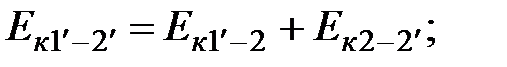
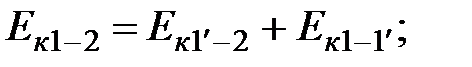
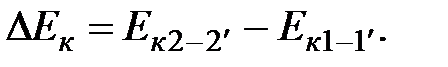
Массы жидкости в отрезках струйки 2-2' и 1-1' равны, а скорости в сечениях - 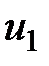 и
и 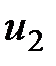 . Таким образом, приращение кинетической энергии
. Таким образом, приращение кинетической энергии
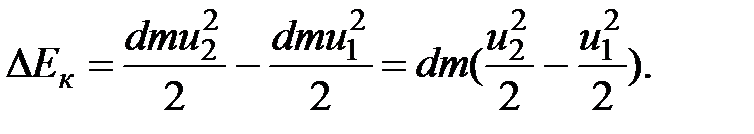 (3.40)
(3.40)
Согласно теореме кинетической энергии (3.27) получим
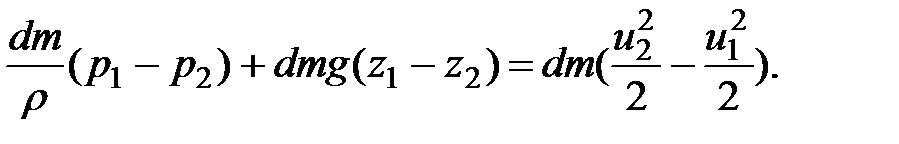 (3.41)
(3.41)
Отнесем все члены уравнения к единице веса 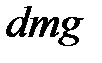 протекающей жидкости, т.е. разделим все члены уравнения (3.41) на
протекающей жидкости, т.е. разделим все члены уравнения (3.41) на 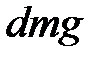 :
:
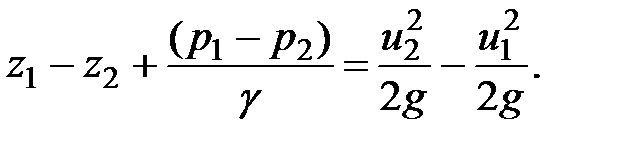 (3.42)
(3.42)
Произведем перегруппировку членов уравнения (3.42) применительно к каждому из сечений 1-1 и 2-2:
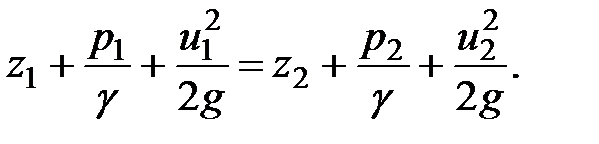 (3.43)
(3.43)
Полученное уравнение называется уравнением Д. Бернулли для струйки идеальной жидкости.
Все члены уравнения Бернулли имеют линейную размерность. Члены уравнения 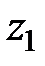 , и
, и 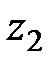 - геометрические высоты положения центров живых сечений относительно плоскости сравнения.
- геометрические высоты положения центров живых сечений относительно плоскости сравнения.
Установив пьезометры в сечениях 1-1 и 2-2, уровень жидкости в них поднимается на высоты 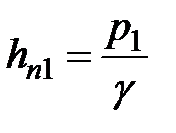 и
и 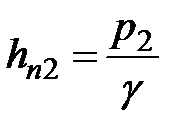 . Члены
. Члены 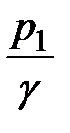 и
и 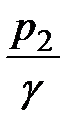 пьезометрические высоты, которые соответствуют гидростатическим давлениям
пьезометрические высоты, которые соответствуют гидростатическим давлениям 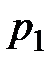 и
и 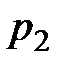 в сечениях 1-1 и 2-2.
в сечениях 1-1 и 2-2.
Члены уравнения 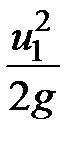 и
и 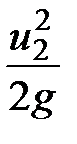 - скоростные высоты.
- скоростные высоты.
Сумма всех трех членов уравнения вдоль струйки постоянна:
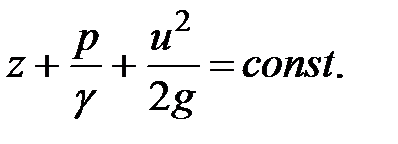
Ранее приводилось понятие удельной энергии. Энергия жидкости, отнесенная к единице веса жидкости, - удельная энергия или напор. Полная энергия струйки складывается из потенциальной и кинетической энергий.
Первых два члена уравнения Бернулли характеризуют потенциальную энергию относительно плоскости сравнения 0-0. Третий член 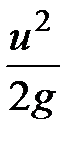 выражает кинетическую энергию. Таким образом, сумма всех членов уравнения будет являться суммой удельных потенциальной и кинетической энергий.
выражает кинетическую энергию. Таким образом, сумма всех членов уравнения будет являться суммой удельных потенциальной и кинетической энергий.
Полная удельная энергия 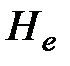 - полный напор, определяемый по формуле
- полный напор, определяемый по формуле
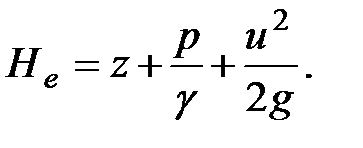 (3.44)
(3.44)
Полная удельная механическая энергия для идеальной жидкости вдоль элементарной струйки является постоянной величиной - 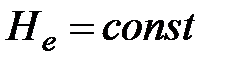 .
.
Члены уравнения Бернулли имеют следующую энергетическую интерпретацию:
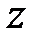 - удельная энергия положения;
- удельная энергия положения;
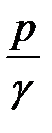 - удельная потенциальная энергия давления;
- удельная потенциальная энергия давления;
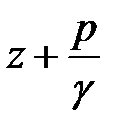 - удельная потенциальная энергия, гидростатический напор;
- удельная потенциальная энергия, гидростатический напор;
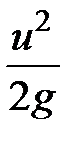 - удельная кинетическая энергия или динамический (скоростной) напор.
- удельная кинетическая энергия или динамический (скоростной) напор.
Удельная потенциальная или кинетическая энергия в разных сечениях по длине струйки могут изменять свои величины, однако сумма их вдоль рассматриваемой идеальной струйки жидкости остается постоянной.
Если все члены умножить на единицу веса 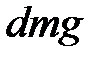 , то получим сумму полной механической энергии, которая будет постоянна для всех сечений.
, то получим сумму полной механической энергии, которая будет постоянна для всех сечений.
Таким образом, уравнение Бернулли для струйки идеальной жидкости при ее установившемся движении выражает закон сохранения механической энергии.
Дата добавления: 2016-02-27; просмотров: 1041;
