Пространственная контактная задача
Контактное взаимодействие
Вопрос контакта двух тел является определяющим при оценке долговечности движущихся деталей механизмов и соединений, поскольку возникающие в процессе взаимодействия напряжения и деформации в конечном итоге формируют предел усталостной прочности материала и его выносливость к воздействию нагрузок. В теории контактного взаимодействия при этом рассматриваются трехмерная (пространственная) и двумерная (плоская) контактные задачи.
Пространственная контактная задача
Пространственная задача заключается в определении напряжений и деформаций двух тел произвольной формы, которая упрощенно сводится к элементам эллипсоидов с главными радиусами кривизны ρ1 и ρ2. Схема взаимодействия представлена на рис. 1.
 |



 Р
Р
 |



 θ
θ
ρ1’ ρ1’’
 |  | ||||
 |
 ρ2’ ρ2’’
ρ2’ ρ2’’

 |



 a P
a P
 |



 b
b
 |
Рис. 1 К рассмотрению пространственной контактной задачи
Угол θ является углом между соответствующими главными радиусами кривизны поверхности контактирующих тел. В результате деформации при сжатии силами Р тела будут касаться друг друга не в точке, по некоторой эллиптической площадке с осями a и b.
Контактное напряжение на площадке согласно теории упругости будет равно:
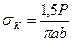
Большая и малая полуоси эллиптической площадки равны соответственно:
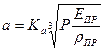 ;
;
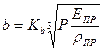 .
.
Деформация тел в области контакта определяется следующим образом:
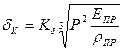
Приведенный радиус кривизны контактирующих тел:
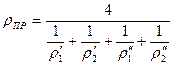
Приведенный модуль упругости:
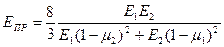 ,
,
где Е1 и μ1 – модуль упругости и коэффициент Пуассона материала первого тела, Е2 и μ2 – модуль упругости и коэффициент Пуассона материала второго тела; коэффициенты Ка , Кb\ , Кδ являются функциями угла θ.
В частном случае, когда одно из тел является шаром, а другое – плоскостью, приведенные выше формулы для напряжения и деформации (применительно к шару) упрощаются:
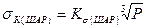 ;
; 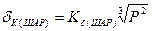 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Шероховатость поверхности детали | | | Первая медицинская помощь при переломах. Правильно оказанная первая помощь при переломах почти в 2 раза сокращает количество возможных осложнений |
Дата добавления: 2016-02-24; просмотров: 673;
