Тербелістер мен толқындар. Оларды сипаттайтын кинематикалық параметрлер.

Табиғат пен техникада қайталанып отыратын физикалық процестер кездеседі. Тербелістің кез келген ортада таралуын толқын деп атайды. Оларға: дыбыс толқындары, сағат механизмнің жұмысы, тізбектегі айнымалы ток, электромагниттік тербелістер және т.б. жатады.

Жалпы физика курсында көбінесе тек бірдей қайталанып отыратын процестерді қарастырып, оның негізгі кинематикалық теңдеулерін жазатын боламыз.

Периодтық қозғалыс деп әрбір циклі дәлме-дәл кез келген басқа циклін қайталап отыратын қозғалысты атайды. Бір цикл ұзақтығын период деп атайды.

Тербелмелі қозғалысты ерікті және еріксіз деп екіге бөледі. Ерікті қозғалыста сыртқы күштің әсерінсіз өз бетінше қозғалыс циклін қайталап отырады. Мұндай тербелістерді еркін тербелістер деп атайды.

Өз бетінше периодтық қозғалыстар жасай алатын немесе тербелетін осы тәрізді денелер немесе денелер жүйесін (материалдық нүктелер жиынтығын) тербелмелі жүйелер деп атаймыз.

Тербелістерді зерттеуді біз механикалық жүйелердің ең қарапайым түрлері: математикалық маятник, физикалық маятник, серпелі маятник, терблмелі контурды қарастырамыз.

Математикалық маятник және оның кинематикасы. Математикалық маятник деп ауырлық центрі іліну нүктесінен төмен болатындай етіп ілінген кез келген денені айтады.

Еркін тербелістерді жасай алатын кез келген системаның орнықты тепе-теңдіік қалпы болады. Математикалық маятник үшін бұл қалып оның ауырлық центрі мен іліну нүктесі вертикалдық бойында және ауырлық центрі іліну нүктесінен төмен орналасатын жағдайға сәйкес келеді.

Егер біз маятникті тепе-теңдік қалпынан шығаратын болсақ, онда тепе-теңдік қалпының оң жағына, бір сол жағына шығып, тербеле бастайды. Маятниктің тепе-теңдіктен ең үлкен ауытқуын тербелістің амплитудасы деп атайды. Амплитудданың бастапқы қозғалыс шартына тәуелділік қасиеті барлық тербелмелі қозғалыстарға тән деуге болады.

Тербелмелі қозғалыстың периодтылығын (ырғақтылығын) сипаттайтын Т шамасын тербелістің периоды деп атайды. Тербелістің периодын толық бір тербеліске кеткен уақытпен өлшейді.

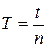(1)

мұндағы n- тербеліс саны, t- сол n тербеліске кеткен уақыт.

Тербелмелі қозғалыстың қайталанғыштық жылдамдығын сипаттайтын шаманы оның 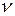жиілігі деп атайды.

(2)

Дене тербелісінің жиілігін бірлік уақыттағы толық тербелістер санымен өлшейді. Тербеліс жиілігі ретінде герц (Гц) алынады. 1Гц=1 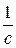; 1Гц=1 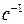. Герц деп бір секунд ішінде бір толық тербеліс жасайтын тербелістің жиілігі алынады.

Сонымен тербелмелі қозғалысты сипаттайтын алғашқы үш шама: тербеліс периоды Т, тербеліс жиілігі 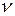және тербеліс амплитудасы А.

Материалдық нүктенің (дененің) тұрақты амплитудада өтетін тербелістерін өшпейтін, ал бірте-бірте азайып отыратын амплитудада өтетін тербелістерді өшетін тербелістер деп атайды.

Тербелістің пайда болуының бірінші қажетті шарты материалдық нүктенің (дененің) орнықты тепе-теңдік қалпына қарағанда бас артық (кинетикалық немесе потенциалдық) энергиясының болуы болып табылады.

Ал 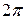секунд ішінде жасалатын тербеліс санын циклдік (дөңгелек) жиілік ( 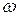, Гц) деп атайды.

(3)

Әрбір уақыт мезетіндегі тербелістегі нүктенің координата фазасымен ( , рад, градус) сипатталады.

(4)

Мұндағы 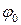- бастапқы фаза, яғни 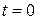мезеттегі фазаның мәні.

Тепе-теңдіктен ауытқытылған математикалық маятникке, жіптің керілу күшіі – Т, ауырлық күші P=mg, және қалпына келтіруші күш F әжіптің реакция күші әсер етеді. (1-cурет)

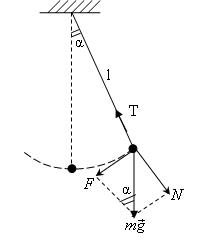
1-сурет

Қалпына келтіруші күштің моменті

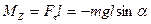(3)

мұндағы 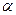- маятниктің тепе-теңдіктен ауытқушы бұрышы, 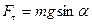- қалпына келтіруші күш, l –маятник жібінің ұзындығы, g – еркін түсу үдеуі, 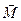мен ауытқу (псевекторлар) векторларының бағыттары бір-біріне қарама-қарсы болғандықтан (2) теңдеуінің алдына «-» таңбасы қойылады.

Қатты дененің динамикасының 2-ші заңы бойынша

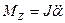(3)

мұндағы J- маятниктің инерция моменті. Енді (2), (3) теңдеулерінен

(4)

Маятниктің тепе-теңдіктен аз ауытқыған жағдайы үшін 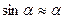және тең екендігін ескере отырып (4) теңдеуді

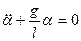(5)

мұндағы 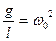деп белгілеп

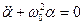(6)

жазып, бұл теңдеуді тербелістің дифференциалдық теңдеуімен салыстырсақ, онда математикалық маятниктің гармоникалық тербелісінің

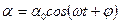(7)

гармоникалық заңы түрінде жазуға болады.

Сонда

,

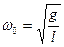ал периоды

(8)

Бұл теңдеу математикалық маятник үшін жазылған Томсон формуласы деп атайды.

Физикалық маятник.. Қатты дене (2 сурет ) ауырлық күшінің әсерінен горизонталь бағытта С масса центрімен сәйкес келмейтін О нүктесінің маңында тербелмелі қозғалысқа түседі. О нүктесін ілу нүктесі деп атайды. Қалпына келтіруші күштің моменті:

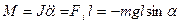
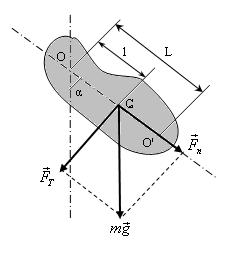
2-cурет

мұндағы J- ілу нүктесі арқылы өтетін оське қатысты инерция моменті, 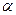- маятниктен тепе-теңдіктен ауытқу бұрышы, 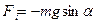- қалпына келтіруші күш, l=OC маятниктің масса центрі мен ілу нүктесінің аралығы.

Динамиканың екінші заңы бойынша қалпына келтіруші күш үшін

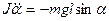
сонда 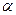-аз мәні үшін

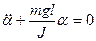
физикалық маятник гармоникалық тербеліс жасайды.

мұндағы 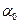- тербелістің циклдік (дөңгелек) жиілігінің амплитудасы

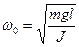
периоды

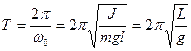(9)

мұндағы 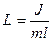- физикалық маятниктің келтірілген ұзындығы деп аталады.

ОС түзуінің бойында жатқан О ілу нүктесінен келтірілген ұзындыққа L тең аралықта жатқан О' нүктесін физикалық маятниктің тербелу центрі деп атайды. Физикалық маятниктің ілу нүктесі мен тербеліс центрілерін өзара алмастыруға болады. Бұл жағдайда физикалық маятниктің тербеліс периоды өзгермейді.

Жоғарыдағы (8.9) теңдеуді физикалық маятник үшін Томсон формуласы деп атайды.

Серпелі маятник – абсолютті серпімді серпеге ілінген массасы m система серпімді күштің әсерінен түзусызықты гармоникалық қозғалыс жасайды (3-сурет)

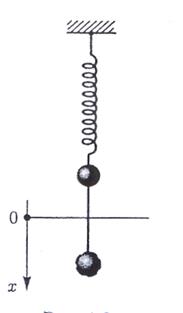
3 сурет

Маятникті қалпына келтіруші күші деформацияланған серпенің ығысу шамасы тура пропорционал болады.

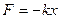
мұндағы k- серпенің қатаңдығы.

Маятниктің қозғалыс теңдеуі

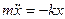
дифференциалдық теңдеуі

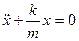немесе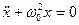

Серпімді күштің әсерінен ол вертикаль тік бағытта гармоникалық тербеліс жасайды.

циклдік (дөңгелек) жиілігі

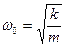
периоды

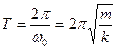(10)

Бұл (10) теңдеуді серпелі маятник үшін Томсон формуласы деп атайды.

Тербелістегі нүктенің берілген уақыт мезетіндегі тепе-теңдік қалпына қатысты орын сипаттайытн шаманы ығысу деп атайды.

Ығысуды тербелістегі нүктенің орнықты тепе-теңдік қалпынан оның осы уақыт мезетіндегі орнына дейінгі қашықтықпен өлшейді.

А – амплитула сан мәні жағынан тербелістегі нүктенің орнықты тепе-теңдік қалпынан ең үлкен 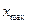ауытқуына тең шама

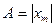
Тербелістегі нүктенің берілген уақыт мезетіндегі орны да, бағытын да сипаттайтын 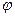шаманы тербілістің фазасы деп атайды. Тербелістің фазасын нүктенің тербелісі басталғаннан бері периодтың қандай бөлігінің өткендігін көрсететін санымен өлшейді. Фазаның ығысудан айырмашылығы тек оның қозғалысының бағытын көрсете алатындығында емес.

Егер ығысу тербелістердің амплитудасымен байланысты болса, ал фаза оған тәуелсіз болады. Фазаның көмегімен бірдей периодтарымен және бірдей амлитудаларымен өтіп жатқан тербелістердің айырмашылығымен тағайындауға да болады.

Екі тербеліс бірдей периодпен (жиілікпен) өтіп жататын болса, онда олардың арасындағы фазалар айырымы тербелістердің өне бойында өзгеріссіз қалады.

Егер нүктенің тербелістері 0 немесе бірдей фазалар айырымымен өтетін болса, онда олар бірдей фазаларда тербеледі.Тербелмелі нүктелер өне бойы бір бағытта қозғалатын болса, онда олардың фазалары бірдей болады. Мұндай тербелістерді синхронды тербелістер деп, ал екі нүктенің тербелістері ½ фазалар айырымымен өтетін болса, онда оларды қарама-қарсы фазалар деп атайды. Тербелмелі нүктелер өне бойы қарама-қарсы бағыттарда қозғалатын болса, онда олардың фазалары қарама-қарсы болады.

Ығысу және фазамен қатар термелмелі нүктенің лездік күйін оның 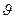қозғалыс жылдамдығымен а үдеуі де сипаттайды. Өйткені бұл шамалар өне бойы уақыт бойынша өзгеріп отырады.

Қозғалыс 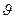жылдамдығы тепе-теңдік қалыпта ең жоғарғы мәніне ие болса, ал шекті нүктеде ол 0-ге тең болады. Ал а үдеу тепе-теңдік қалыпта 0-ге шекті қалыпта ең үлкен мәнді қабылдайды.