Гармоникалық тербелістерді қосу.
1. Бағыттары мен жиіліктері бірдей гармоникалық тербелістерді қосу.
Тербелетін денеде бірнеше тербелмелі процестер жүруі мүмкін. Сондықтан осындай тербелістердің қорытқы амплитудасын анықтау керек болады.
Жиіліктері мен бағыттары бірдей гармоникалық тербелістерді қосу үшін векторлық диаграмма әдісін қолданады (9 сурет).

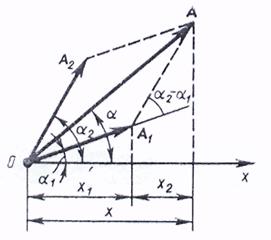
9-сурет
Қорытқы ығысу амплитудасы мен бастапқы фазасы
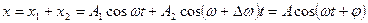 (31)
(31)
мұндағы
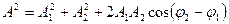 (32)
(32)
Бастапқы фаза
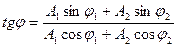 (33)
(33)
Қорытқы гармоникалық тербелістің амплитудасы фаза айырымына  тәуелді болады.
тәуелді болады.
Енді (32), (33) теңдеулерді талдайтын болсақ, онда
1) 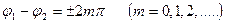
Қорытқы тербелістің амплитудасы жеке тербелістердің амплитудаларының алгебралық қосындысына тең болады:
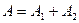
2) 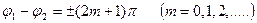
Қорытқы тербелістің амплитудасы жеке тербелістер амплитудасның айырымына тең
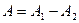 .
.
Бір бағытта тербелетін қосылатын екі тербелістің жиіліктері бір-бірінен сәл өзгешелеу 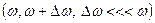 . Қорытқы тербелістің амплитудасы периодты түрде өзгереді, мұндай тербелісті соғу (10 сурет) деп атайды.
. Қорытқы тербелістің амплитудасы периодты түрде өзгереді, мұндай тербелісті соғу (10 сурет) деп атайды.
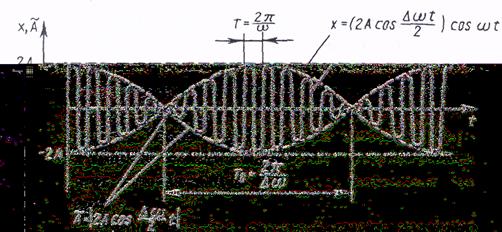
10- сурет

Сонда
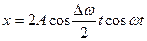 ()
()
Мұндағы  соғу амплитудасы деп, ал
соғу амплитудасы деп, ал 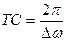 соғу периоды деп атайды.
соғу периоды деп атайды.
Өшетін тербелістер.
Реал (нақты) тербеліс жүйесінде кедергі күші 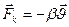 әсерінен нүктенің энергиясы imкi энергияга айналады, соның салдарынан уақыт өтуімен бipre оның тербеліс амплитудасы азаяды. Мұндай козғалыс мына дифференциалдық теңдеумен сипатталады:
әсерінен нүктенің энергиясы imкi энергияга айналады, соның салдарынан уақыт өтуімен бipre оның тербеліс амплитудасы азаяды. Мұндай козғалыс мына дифференциалдық теңдеумен сипатталады:

мұндағы 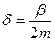 - өшу коэффициенті,
- өшу коэффициенті, 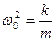 - ортаның кедергісі болмағанда (
- ортаның кедергісі болмағанда ( 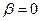 ) жүйенің жасайтын еркін тербелістерінің жиілігі.
) жүйенің жасайтын еркін тербелістерінің жиілігі.
Тербеліс теңдеуі:

мұндағы 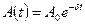 - өшетін тербелістің амплитудасы, Ао— бастапкы амплитуда (11-сурет).
- өшетін тербелістің амплитудасы, Ао— бастапкы амплитуда (11-сурет).
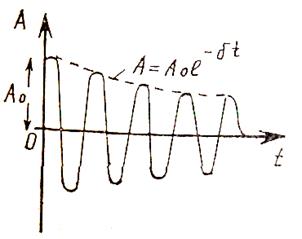
11 - сурет
Бip-бipiнен периодқа сәйкес уакытқа ажыратылатын амплитудалар катынасының логарифмі логарифмдік декремент деп аталады:
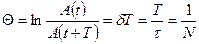
Амплитуда е ~2,7 есе кемитін 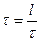 (релаксация уақыты) уақыт ішінде жүйе
(релаксация уақыты) уақыт ішінде жүйе 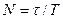 тербеліс жасап үлгереді. Тербелмелі жүйені сипаттау үшін сапалық (Q) деп аталатын шама енгізеді:
тербеліс жасап үлгереді. Тербелмелі жүйені сипаттау үшін сапалық (Q) деп аталатын шама енгізеді:
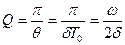
Өшетін тербелістің периоды мен жиілігі мынаған тең:
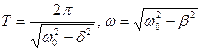
Орта кедергісі аз болған жағдайда, яғни 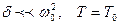 .
.
Еріксіз тербелістер деп тербелмелі жүйеде периодты түрде өзгеретін 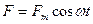 күштің әсерінен пайда болатын өшпейтін тербелістерді айтады.
күштің әсерінен пайда болатын өшпейтін тербелістерді айтады.
Серіппелік маятниктің қозғалысының дифференциалдық теңдеуі былай жазылады:
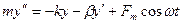
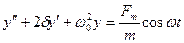
мұндағы 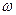 -сыртқы әсер ететін күш жиілігі. дифференциалдық теңдеулер теориясынан біртекті емес теңдеудің жалпы шешімі оған сәйкес келетін біртекті теңдеудің жалпы шешімі мен біртекті емес теңдеудің
-сыртқы әсер ететін күш жиілігі. дифференциалдық теңдеулер теориясынан біртекті емес теңдеудің жалпы шешімі оған сәйкес келетін біртекті теңдеудің жалпы шешімі мен біртекті емес теңдеудің  дербес шешімінің қосындысына тең.
дербес шешімінің қосындысына тең.
( 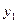 ) қосылғышы тербелістің орнығуы деп атайды (12- сурет), ол бастапқы кезеңде ғана роль атқарып, уақыт өткен сайын кемиді, оны ескермеуге де болады.
) қосылғышы тербелістің орнығуы деп атайды (12- сурет), ол бастапқы кезеңде ғана роль атқарып, уақыт өткен сайын кемиді, оны ескермеуге де болады.
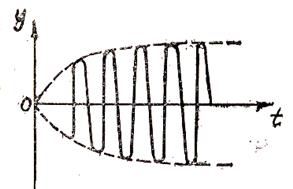
12- Сурет
Сонымен (y) функциясы орныққан еріксіз тербелістерді сипаттайды:
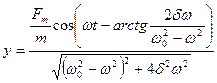
Еріксіз тербелістің амплитудасы мәжбүр теуші күштің 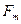 амплитудасына пропорционал және оның жиілігіне тәуелді:
амплитудасына пропорционал және оның жиілігіне тәуелді:
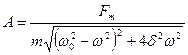 .
.
Еріксіз тербелістер фазасы бойынша мәжбүр теуші күштен қалып қояды да, әрі қалу шамасы мәжбүр етуші күш жиілігі 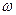 -ға тәуелді.
-ға тәуелді.
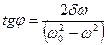
Сыртқы күштің 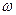 жиілігі жүйенің меншікті
жиілігі жүйенің меншікті  жиілігіне жақындағанда еріксіз тербеліс амплитудасының ең үлкен мәніне жету құбылысы резонанс деп, ал оған сәйкес келетін жиілік резонанстық жиілік деп аталады.
жиілігіне жақындағанда еріксіз тербеліс амплитудасының ең үлкен мәніне жету құбылысы резонанс деп, ал оған сәйкес келетін жиілік резонанстық жиілік деп аталады.
Механикалық толқындар.Серпімді ортада тербелістің таралуын механикалық толқын деп атайды. Орта бөлшектерінің тербеліс бағыты толқынның таралу бағытымен бағыттас болса, онда толқындарды қума, ал толқынның таралу бағытына перпендикуляр бағытталған болса, көлденең толқындар деп атайды.
Толқын фронты (немесе толқындық бет ) деп, бірдей фазаларда тербелетін нүктелердің геометриялық орнын айтамыз. ТОлқын фронтының түріне байланысты толқындар жазық және сфералық болып бөлінеді.
Бірдей фазада тербеліп тұрған екі жақын жатқан нүктенің ара-қашықтығын толқын ұзындығы деп атайды:
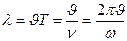
мұндағы Т – тербеліс периоды, 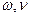 -жиілік.
-жиілік.
Толқын теңдеуін және оның шешімін мына түрде жазуға болады:
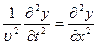 ,
, 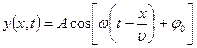 ,
,


мұндағы х – О толқындық көзінен ортанң қарастырып жатқан А нүктесіне дейінгі ара-қашықтық (13- сурет),  - толқындық сан, ол
- толқындық сан, ол  ұзындық бірлігіне қанша толқын жайғасатынын көрсететін сан.
ұзындық бірлігіне қанша толқын жайғасатынын көрсететін сан.
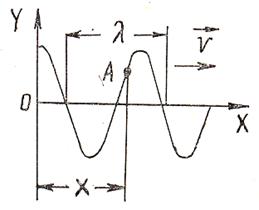
13- сурет
Толқын фазасы тұрақты десек, яғни  , онда фазалық жылдамдық , яғни фазаның орын ауыстыру жылдамдығы:
, онда фазалық жылдамдық , яғни фазаның орын ауыстыру жылдамдығы:
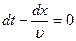 , бұдан
, бұдан 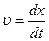 .
.
(1) өрнегі х шамасының арту бағытында таралатын жазықтық, ал (2) сфералық толқынның теңдеуінде r – толқын көзінен ортаның қарастырып отырған нүктесіне дейінгі ара-қашықтық, ал А – толқын көзінен 1-ге тең қашығы сан жағынан амплитудаға тең тұрақты шама. Қума және көлденең толқындардың фазалық жылдамдықтары мынаған тең:
 ,
,

мұндағы E, G – Юнг, ығысу модульдері, 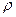 -ортаның тығыздығы.
-ортаның тығыздығы.
Толқын энергиясының тығыздығы ортаның тығыздығына және жиілік пен амплитуданың квадраттарына пропорционал болады:
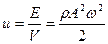
Қандай да болсын бет арқылы бірлік уақыт ішінде толқын тасымалдайтын энергия мөлшері (энергия ағыны) ағынның тығыздығы деп аталады.
Энергия ағынының тығыздығы деп аталатын векторлық шаманың модулі энергия тасымалданатын бағытқа перпендикуляр, берілген нүкте орналасқан бірлік аудан арқылы өтетін энергия ағынына тең, ал бағыты толқынның таралу бағытына сәйкес келеді:
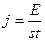
Фазалық жылдамдықт, бағыты толқынның таралу бағытымен дәл келетін вектор ретінде қарастырып, Уомв векторын төмендегі түрде жазуға болады:
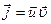
Толқынның берілген нүктедегі қарқындылығы деп, Умов векторының уақыт бойынша орташа мәнін айтады:
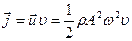 .
.
Дата добавления: 2016-02-24; просмотров: 7558;
