Тербелмелі контурдағы еркін гармоникалық тербеліс
Көптеген электрлік құбылыстардың ішінен периодты түрде өзгеретін электрлік шамалар: заряд, тоқ, электр және магнит өрістері ерекше орын алады. Электромагиниттік тербелісті тудыру мен оны ұстап тұру үшін белгілі бір жүйе (система) қажет. Осындай жүйені тербелмелі контур деп атайды. Ол 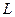 индуктивтік катушкадан, С сыйымдылық конденсатордан және R кедергіден тұрады. Біз тек кедергісі R=0 тең болатын идеал контурды ғана қарастырамыз. Контурда электр тербелісін тудыру үшін конденсатор астарларына
индуктивтік катушкадан, С сыйымдылық конденсатордан және R кедергіден тұрады. Біз тек кедергісі R=0 тең болатын идеал контурды ғана қарастырамыз. Контурда электр тербелісін тудыру үшін конденсатор астарларына 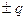 зарядтары беріледі. Сонда
зарядтары беріледі. Сонда 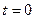 уақыт мезетінде конденсатор астарларының арасында энергиясы
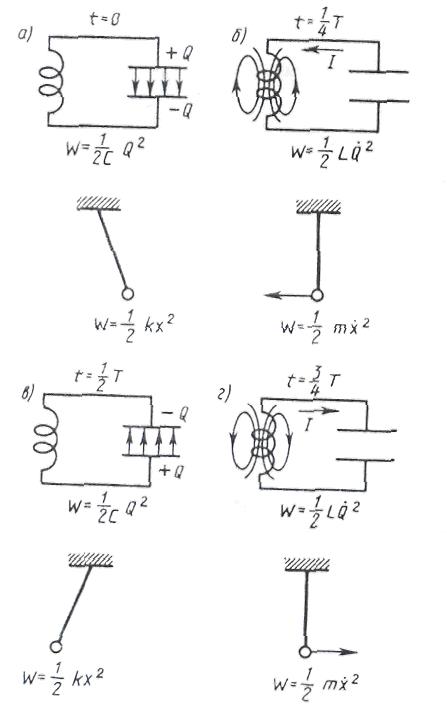
уақыт мезетінде конденсатор астарларының арасында энергиясы 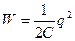 тең электр өрісі пайда болады. (8, а сурет).
тең электр өрісі пайда болады. (8, а сурет).
Енді контурды 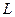 индуктивтік катушка арқылы жүйені тұйықтайтын болса, онда конденсатор зарядсызданады да, тізбектен
индуктивтік катушка арқылы жүйені тұйықтайтын болса, онда конденсатор зарядсызданады да, тізбектен 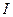 тоғы жүреді. Қорытындысында электр өрісінің энергиясы азайып, магнит өрісінің энергиясы өседі. Энергияның сақтылу заңы бойынша
тоғы жүреді. Қорытындысында электр өрісінің энергиясы азайып, магнит өрісінің энергиясы өседі. Энергияның сақтылу заңы бойынша

Тізбектегі актив кедергідегі энергиясын ескермейтін болсақ, онда 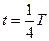 уақыт мезетінде конденсатор толық зарядсызданады да, электр өрісінің энергиясы магнит өрісінің энергиясына (8, в сурет) айналады. Осы сәттен бастап катушкадағы ток кеми бастайды.
уақыт мезетінде конденсатор толық зарядсызданады да, электр өрісінің энергиясы магнит өрісінің энергиясына (8, в сурет) айналады. Осы сәттен бастап катушкадағы ток кеми бастайды.
8-сурет
Катушкадағы магнит өрісі азаяды да Ленц ережесіне сәйкес индукциялық электроқозғаушы күш пайда болады. Конденсатор қайтадан зарядталып, онда электр өрісі пайда болып, токты азайтуға тырысады. Уақыттың 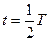 мезетінде конденсатор толық зарядталады (8, в сурет). Әрі қарай процесс қайталанып ток кері бағытта (8, г сурет) жүреді.
мезетінде конденсатор толық зарядталады (8, в сурет). Әрі қарай процесс қайталанып ток кері бағытта (8, г сурет) жүреді.
Электр тізбегінде тербелмелі қозғалысты механикалық тербеліспен салыстыруға болады (8, а, б, в, г сурет).
Кирхгофтың екінші ережесіне сәйкес 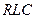 тізбегі үшін
тізбегі үшін
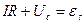 (22)
(22)
мұндағы 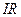 кедергідегі кернеу,
кедергідегі кернеу, 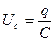 - конденсатордағы кернеу,
- конденсатордағы кернеу, 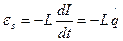 - контурдағы өздік индукциялық электрқозғаушы күш.
- контурдағы өздік индукциялық электрқозғаушы күш.
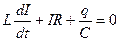 (23)
(23)
Осы (23) теңдеуді 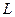 -ге бөліп,
-ге бөліп, 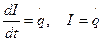 ескере отырып, тізбектегі
ескере отырып, тізбектегі 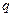 зарядының тербелісінің дифференциялдық теңдеуін
зарядының тербелісінің дифференциялдық теңдеуін
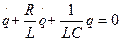 (24)
(24)
Қарастырып отырған тербелмелі контурда сыртқы ЭҚК жоқ, сондықтан тербеліс еркінтербеліс болып табылады. Егер 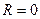 тең болса, контурдағы электромагниттік тербеліс еркін тербеліс, болады. Сонда (24) теңдеуінен контурдағы гармоникалық
тең болса, контурдағы электромагниттік тербеліс еркін тербеліс, болады. Сонда (24) теңдеуінен контурдағы гармоникалық 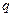 зарядының тербелісінің дифференциалдық теңдеуі
зарядының тербелісінің дифференциалдық теңдеуі
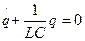 (25)
(25)
Жоғарыдағы (11) теңдеуідегі 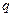 заряды мынадай заңдылық бойынша гармоникалық тербеліс жасайды.
заряды мынадай заңдылық бойынша гармоникалық тербеліс жасайды.
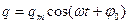 (26)
(26)
мұндағы 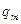 конденсатордағы
конденсатордағы 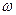 дөңгелек жиілікте тербелетін зарядтың амплитудалық мәні. Дөңгелек жиілік
дөңгелек жиілікте тербелетін зарядтың амплитудалық мәні. Дөңгелек жиілік
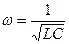 (27)
(27)
период
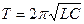 ; (28)
; (28)
Бұл (28) өрнекті электромагниттік өрнек үшін Томсон формуласы деп атайды.
Тербелмелі контурдағы ток күші
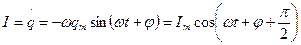 (29)
(29)
мұндағы 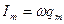 токтың амплитудалық мәні.
токтың амплитудалық мәні.
Контурдағы конденсатор астарларындағы кернеу
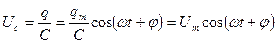 (30)
(30)
Мұндағы 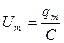 кернеу амплитудасы.
кернеу амплитудасы.
Сонымен (26) және (29) теңдеудерінен контурдағы 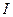 ток, ондағы
ток, ондағы 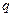 заряд тербелісі фаза жағынан
заряд тербелісі фаза жағынан 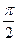 -ге бұрын жүреді. Яғни контурдағы ток ең үлкен
-ге бұрын жүреді. Яғни контурдағы ток ең үлкен 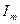 мәніне жеткенде заряд пен кернеу нольге тең немесе керісінше болады. Бұл өзара байланысты энергияның сақталу заңынан шығарып алуға болады. Контурдағы еркін электромагниттік тербеліс өшпейтін тербеліс.
мәніне жеткенде заряд пен кернеу нольге тең немесе керісінше болады. Бұл өзара байланысты энергияның сақталу заңынан шығарып алуға болады. Контурдағы еркін электромагниттік тербеліс өшпейтін тербеліс.
Дата добавления: 2016-02-24; просмотров: 5786;
