Основные логические операции алгебры логики
Для математического описания работы вычислительного устройства, синтеза и анализа схем широко используется алгебра логики. Алгебра логики – это часть математической логики обычно называемой исчислением высказываний. Высказывание – это всякое предложение, в котором содержится смысл утверждения (истинности) или отрицания (ложности). Одно и тоже высказывание не может быть одновременно истинным и ложным. Рассматриваются только два значения высказывания: истинное или ложное (1 или 0). Основными логическими операциями являются: логическое отрицание, логическое сложение, логическое умножение и сложение по модулю 2.
Логическое отрицание (операция НЕ, инверсия)



 Имеем некоторое высказывание А, отрицание этого высказывания обозначается А (читается не А). Если А истинно (А=1), то А – ложно А=0) и наоборот. Таким образом, для логического отрицания справедливо следующее правила: 0=1; 1=0.
Имеем некоторое высказывание А, отрицание этого высказывания обозначается А (читается не А). Если А истинно (А=1), то А – ложно А=0) и наоборот. Таким образом, для логического отрицания справедливо следующее правила: 0=1; 1=0.
Логическое умножение (операция И, конъюнкция)
Операцию логического умножения А и В обозначают А В или А · В (читают: А и В). Высказывание А^ В истинно только в том случае, если А и В истинно (А=1), (В=1), в других случаях это высказывание ложно.
Таблица истинности:
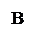
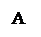
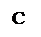



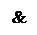

 &
&
Логическое сложение (операция ИЛИ, дизъюнкция)

 Операция логического сложения А и В обозначается А V В (читается: А или В). Высказывание А V В = 1 истинно в том случае, когда истинно хотя бы одно из переменных.
Операция логического сложения А и В обозначается А V В (читается: А или В). Высказывание А V В = 1 истинно в том случае, когда истинно хотя бы одно из переменных.
Таблица истинности:
| А | В | 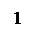 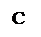 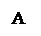   А V В А V В
|
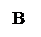  0 0
| ||
 1 1
| ||
| А | В | А 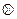 В В
|
Сложение по модулю 2 (исключающее ИЛИ)
Операция сложения по модулю 2 А и В; обозначают А 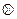 В. А
В. А 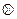 В = 1 высказывание истинно в том случае, когда одно из переменных истинно, в других случаях – оно ложно. Таблица истинности:
В = 1 высказывание истинно в том случае, когда одно из переменных истинно, в других случаях – оно ложно. Таблица истинности:
На основе этих высказываний можно представить любое сложное высказывание, то есть любую логическую связь можно выразить логическими операциями сложения, умножения, отрицания.
Дата добавления: 2016-02-24; просмотров: 930;
