Пример расчета центрально сжатой сквозной колонн
В данном примере нагрузка и длина колонны имеют другие значения, чем в п.4.4.
Определение размеров сечения колонны
Колонна состоит из двух ветвей (два прокатных двутавра), соединенных планками.
Материал колонн – сталь С255. Для нее по табл. 51 СНиПа II-23-81* определим, что расчетное сопротивление растяжению, сжатию и изгибу по пределу текучести Ry = 24 кН/см2.
В расчетной схеме имеем шарнирное крепление главных балок с колонной, и по заданию шарнирное крепление колонны к железобетонному фундаменту.
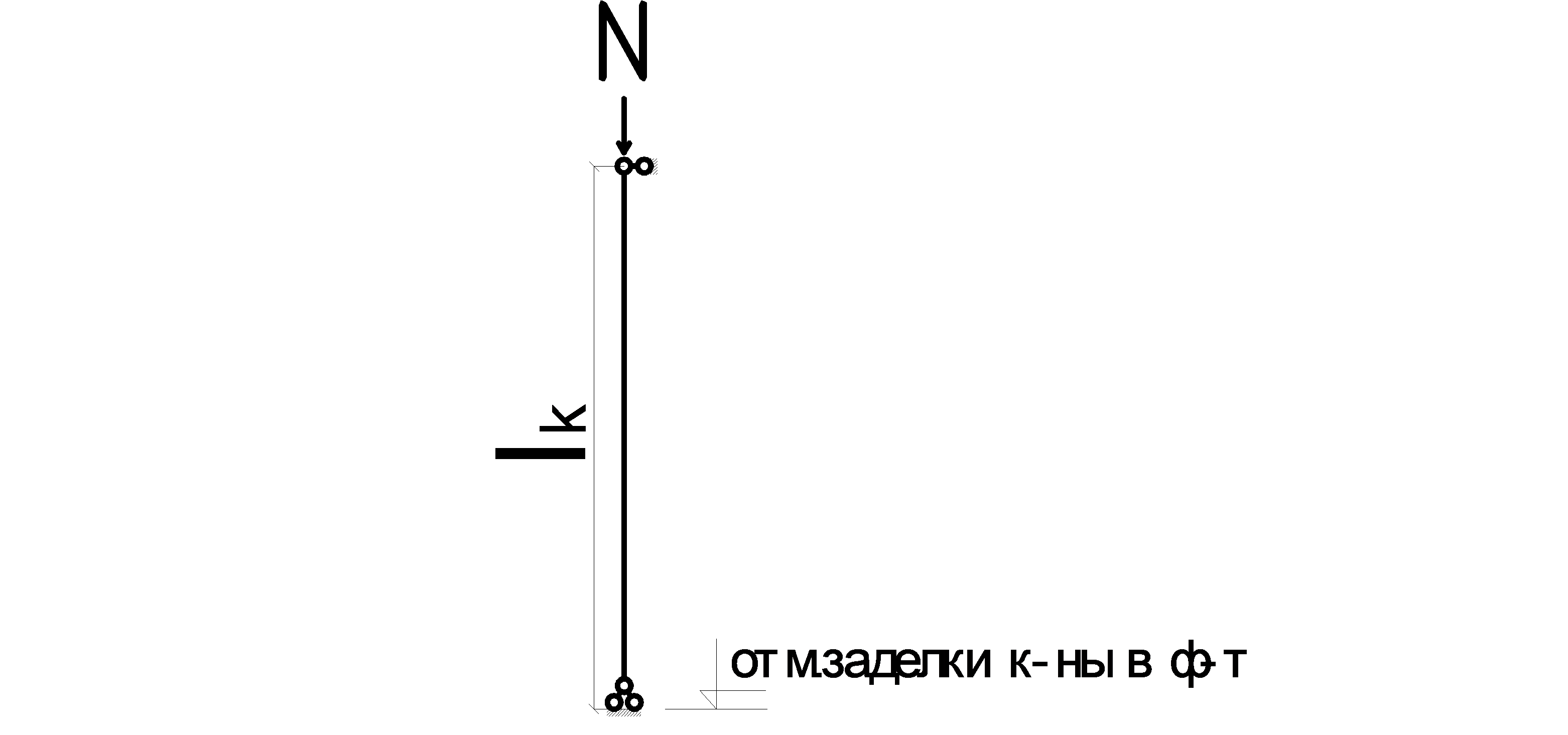 Такое крепление возможно только при условии устройства вертикальных связей между колоннами.
Такое крепление возможно только при условии устройства вертикальных связей между колоннами.
Рис.4.15. Расчетная схема колонны
Нагрузка на колонну:
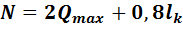
где:
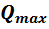 - максимальная поперечная сила в главной балке, действующая на колонну.
- максимальная поперечная сила в главной балке, действующая на колонну.
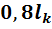 - собственный вес колонны (0,8 – эмпирический коэффициент, учитывающий собственный вес колонны кН/м)
- собственный вес колонны (0,8 – эмпирический коэффициент, учитывающий собственный вес колонны кН/м)
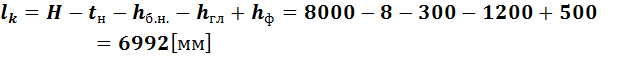
где:
H = 8000мм – заданная отметка верха настила,
tн = 8мм – толщина настила в принятом варианте,
hб.н. = 300мм – принятая по сортаменту высота балки настила,
hгл = 1200мм – высота главной балки,
hф = 500мм – заглубление колонны ниже нулевой отметки.
Тогда: 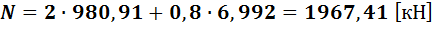
- Определяем требуемую площадь поперечного сечения стержня колонны:
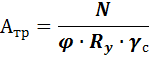
где 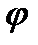 – коэффициент устойчивости, определяется по таблице СНиПа по величине
– коэффициент устойчивости, определяется по таблице СНиПа по величине 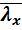 .
.
Задаемся гибкостью колонны относительно материальной оси х в зависимости от получившейся нагрузки на колонну:
При N<2500 кН, λх = 60…90.
При N≥2500 кН, λх = 40…60.
Принимаем гибкость λх = 60.
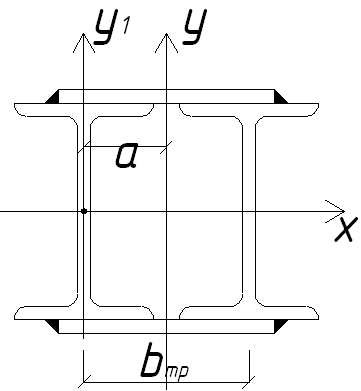
Рис. 4.16. Поперечное сечение сквозной колонны
Условная гибкость 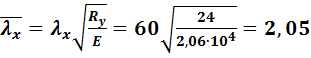
Для принятого сечения (из двух двутавров) определяем тип кривой устойчивости в соответствии с типом сечения – тип «b» /1/ . По таблице коэффициентов устойчивости при центральном сжатии условной гибкости 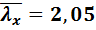 соответствует
соответствует 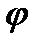 = 0,818.
= 0,818.
Определяем требуемую площадь поперечного сечения:
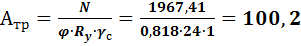 см2
см2
Принимаем сечение колонны из двух двутавров №33 с общей площададью
2·53,8 = 107,6 [см2], ix = 13,5 см.
Определение требуемого расстояния между ветвями колонны
Это расстояние важно для обеспечения устойчивости колонны относительно свободной оси y: чем больше расстояние, тем более устойчива колонна.
Требуемая гибкость относительно свободной оси при гибкости ветви λв = 30 равна:
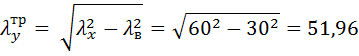
где:
λх = 60 (задались)
λв = 30 – гибкость одной ветви колонны (задались)
Необходимый радиус инерции принятого сечения колонны относительно оси y:

где:
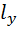 - расчетная длина стержня колонны из плоскости (относительно оси y)
- расчетная длина стержня колонны из плоскости (относительно оси y)
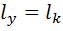 (см. выше)
(см. выше)
С помощью эмпирического коэффициента находим требуемое расстояние:
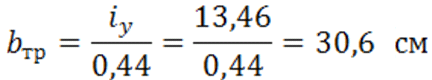
Принимаем b = 31 см
Расстояние в свету между полками двутавров
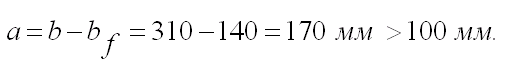
где:
bf – ширина полки ветви колонны (по сортаменту)
a ≥ 100мм – расстояние между ветвями, которое назначается из условия возможности окраски внутренней поверхности ветви.
Проверка устойчивости колонны подобранного сечения.
В плоскости чертежа (относительно оси х):
Проверка по нормальным напряжениям:
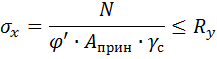
где:
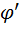 - уточненный коэффициент устойчивости, который считается по истинной гибкости λx
- уточненный коэффициент устойчивости, который считается по истинной гибкости λx
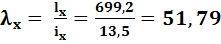
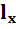 - расчетная длина стержня колонны в плоскости х; в нашем случае
- расчетная длина стержня колонны в плоскости х; в нашем случае
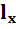 = геометрической длине, так как имеем шарнирное крепление вверху и внизу
= геометрической длине, так как имеем шарнирное крепление вверху и внизу
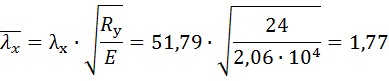
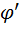 = 0,859
= 0,859
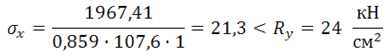
Проверка устойчивости колонны относительно оси y:
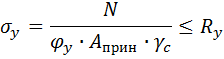
Для определения  находим истинное
находим истинное 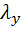
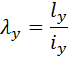
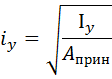
где:
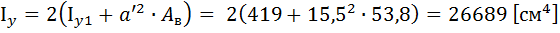 - момент инерции двух ветвей колонны;
- момент инерции двух ветвей колонны;
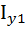 - собственный момент инерции двутавра (сортамент)
- собственный момент инерции двутавра (сортамент)
a’ = a/2= 15,5 см – расстояние от оси у до оси у1, проходящей через центр тяжести двутавра, параллельно оси у
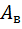 – площадь одного двутавра (сортамент)
– площадь одного двутавра (сортамент)
тогда: 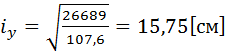
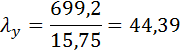
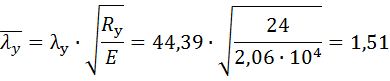
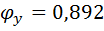
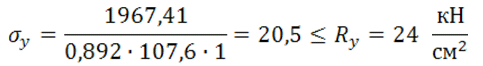
Расчет соединительных планок:
Задаемся шириной планки d = 16 см; толщиной планки td = 0,8 см.
Момент инерции сечения планки относительно собственной оси (х):
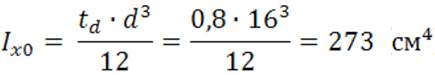
Расстояние в свету между планками:
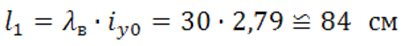
где: 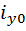 - радиус инерции сечения ветви относительно собственной оси (сортамент);
- радиус инерции сечения ветви относительно собственной оси (сортамент); 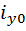 = 2,79
= 2,79
Приведенную гибкость определяем в зависимости от величины 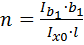
где:
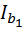 - момент инерции одной ветви относительно собственной оси (у1)
- момент инерции одной ветви относительно собственной оси (у1)
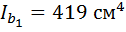
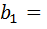 31 см - расстояние между центрами тяжести ветвей колонны.
31 см - расстояние между центрами тяжести ветвей колонны.
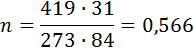
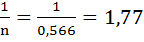 < 5, следовательно, условная гибкость
< 5, следовательно, условная гибкость
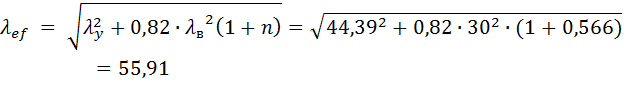
Условно приведенная гибкость:
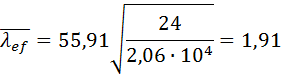
Тогда ϕ= 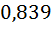
Проверка по нормальным напряжениям:
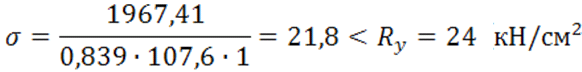
Расчет и конструирование оголовка колонны.
На оголовок колонны опираются две главных балки, поэтому стенку колонны необходимо укрепить ребрами жесткости – вертикально и горизонтально.
Балки опираются на опорную плиту оголовка.
Вид сверху на оголовок
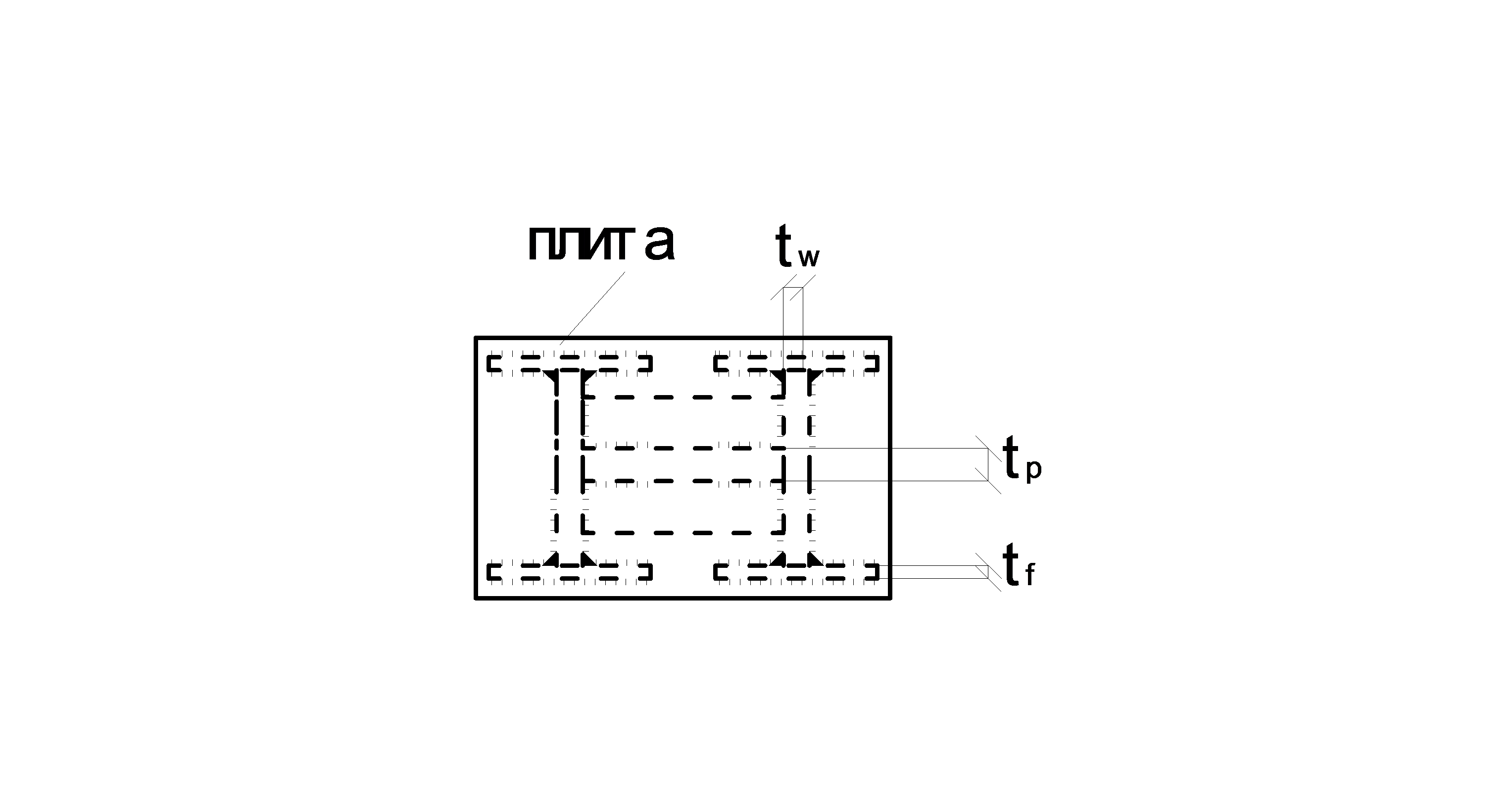
| плита |
| гл. балка |
| N |
| колонна |
Рис. 4.17. Оголовок сквозной колонны
Расчет оголовка сводится к:
1. Определению толщины вертикального ребра.
2. Определению высоты вертикального ребра.
Толщину ребра определяем из расчета ребра на смятие.
Площадь сминаемой поверхности:
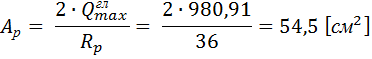
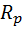 – расчетное сопротивление стали смятию
– расчетное сопротивление стали смятию
Расчетная ширина ребра:
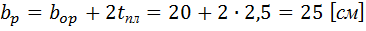
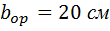 - ширина опорных ребер балок
- ширина опорных ребер балок
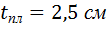 - толщина опорной плиты оголовка
- толщина опорной плиты оголовка
Толщина ребер 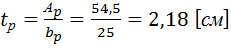
Принимаем толщину ребер 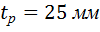 .
.
Задаемся катетом шва kf = 10 мм
Сварные швы будем выполнять полуавтоматической сваркой электродами Э42, выполненными из проволоки сплошного сечения Св-08А со значением 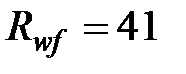 кН/см2. Для стали С255 значение
кН/см2. Для стали С255 значение 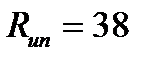 кН/см2.
кН/см2.
Значения коэффициентов  при сварке в нижнем положении равны:
при сварке в нижнем положении равны: 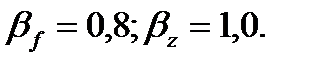
Таким образом, расчетные сопротивления сварного шва по металлу шва и по границе сплавления соответственно будут равны ( по табл.3 СНиП II-23-81*):
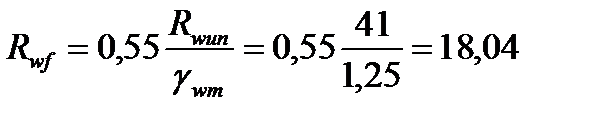 ;
; 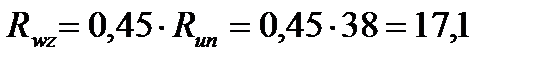 кН/см2 .
кН/см2 .
Значения коэффициентов  при сварке в нижнем положении равны:
при сварке в нижнем положении равны: 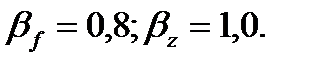
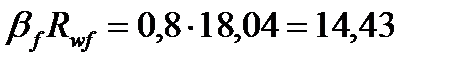 кН/см2,
кН/см2,
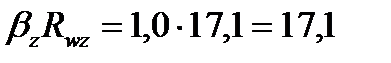 кН/см2,
кН/см2,
Cледовательно, расчетным сечением является сечение по металлу границы сплавления. Тогда длина одного углового шва будет равна ( при kf = 10 мм – для вставки стенки в колонну > 10 мм).
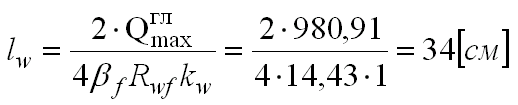
Принимаем hp=lw+1=34+1 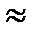 35 см
35 см
Высота ребра равна полной длине шва l = 35 см = 350 мм
Расчет и конструирование базы колонны.
Расчет сводится к:
1. Определению требуемой площади опорной плиты и её размеров в плане.
2. Определению толщины плиты.
3. Определению высоты траверсы.
1) Требуемая площадь опорной плиты:
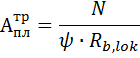
где:
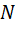 - нагрузка от колонны
- нагрузка от колонны
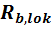 - расчетное сопротивление бетона смятию
- расчетное сопротивление бетона смятию
Опорная плита базы колонны крепится к бетонному или железобетонному фундаменту с помощью анкерных (фундаментных) болтов.
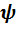 - коэффициент, зависящий от характера распределения нагрузки от колонны по площади смятия
- коэффициент, зависящий от характера распределения нагрузки от колонны по площади смятия
Т.к. имеем равномерно распределенную нагрузку (в первом приближении), 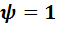

где:
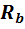 =0,85 кН/см2 - расчетное сопротивление бетона сжатию, которое принимается по СНиПу «Бетонные и железобетонные конструкции» в соответствии с классом заданного бетона (в нашем случае B15).
=0,85 кН/см2 - расчетное сопротивление бетона сжатию, которое принимается по СНиПу «Бетонные и железобетонные конструкции» в соответствии с классом заданного бетона (в нашем случае B15).
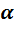 – коэффициент, зависящий от характера опирания опорных плит на фундамент и от класса бетона. При классе бетона ниже B25,
– коэффициент, зависящий от характера опирания опорных плит на фундамент и от класса бетона. При классе бетона ниже B25, 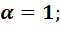
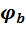 - коэффициент пересчета расчетного сопротивления бетона сжатию к расчетному сопротивлению бетона смятию, который зависит также от класса бетона. В нашем случае
- коэффициент пересчета расчетного сопротивления бетона сжатию к расчетному сопротивлению бетона смятию, который зависит также от класса бетона. В нашем случае 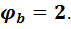
Тогда:
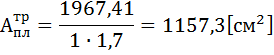
Предварительно определяем размеры опорной плиты в плане, предположив, что она квадратная.
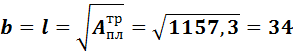
Принимаем размеры плиты, 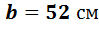
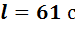 м (по конструктивным соображениям, чтобы консоли были равны их минимальному значению 80мм), тогда
м (по конструктивным соображениям, чтобы консоли были равны их минимальному значению 80мм), тогда
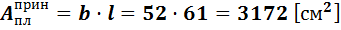

Рис. 4.18. База сквозной колонны
2)Определение толщины опорной плиты:
Плита работает на изгиб от реактивного давления бетона фундамента, приложенного к плите снизу.
Рассчитываем плиту как тонкую пластину. Для этого разбиваем ее на участки 1, 2, и 3 (рис. 4.17).
1 – рассчитывается как пластина, заделанная по четырем сторонам.
2 – как пластина, заделанная по трем сторонам
3 – как консольная пластина (плита)
· Максимальный изгибающий момент на участке 1:
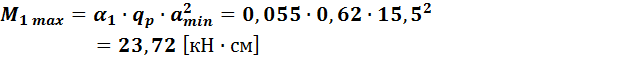
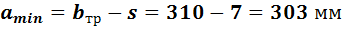 - меньшая из сторон участка
- меньшая из сторон участка
α = 0,055 – коэффициент, принимаемый по таблице метода т. упругости и зависящий от соотношения сторон участка 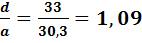
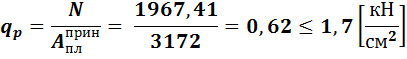
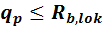
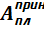 - принятая площадь по округлённым размерам
- принятая площадь по округлённым размерам
· Максимальный изгибающий момент на участке 2 рассчитываем как для консоли или как для пластины, заделанной по трем сторонам:
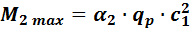
- Зависит от соотношения сторон участка: если 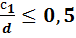 , то рассчитываем момент как для консоли:
, то рассчитываем момент как для консоли:
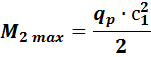
с1 = 80 + 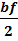 -
-  = 80 +
= 80 + 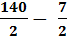 = 146,5 [мм]
= 146,5 [мм]
В нашем случае > 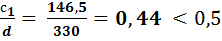 , поэтому считаем по ф-ле как для консоли по формуле:
, поэтому считаем по ф-ле как для консоли по формуле:
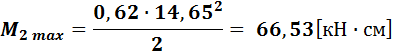
· Максимальный изгибающий момент на участке 3:

Т.к. изгибающий момент на втором участке резко отличается от остальных, необходимо внести изменения в схему опирания плиты добавлением дополнительных диафрагм толщиной 10 мм, чтобы по возможности выровнять значение моментов, что должно привести к облегчению базы.
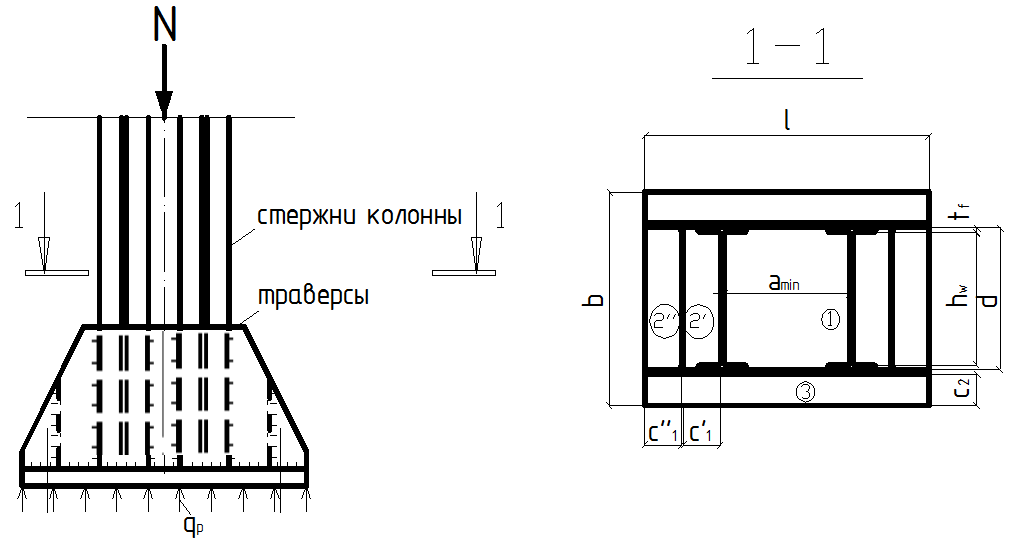
Максимальный изгибающий момент На участке 2’:
· 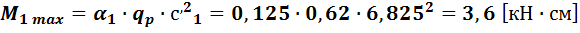
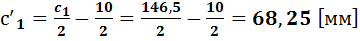 - меньшая из сторон участка
- меньшая из сторон участка
α = 0,125 – коэффициент, принимаемый по таблице метода т. упругости и зависящий от соотношения сторон участка 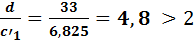
· Максимальный изгибающий момент на участке 2 рассчитываем как для консоли или как для пластины, заделанной по трем сторонам:
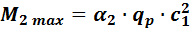
- зависит от соотношения сторон участка: если 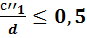 , то рассчитываем момент как для консоли:
, то рассчитываем момент как для консоли:
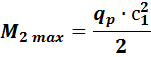

В нашем случае 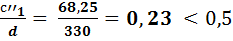 , поэтому считаем по ф-ле как для консоли по формуле:
, поэтому считаем по ф-ле как для консоли по формуле:
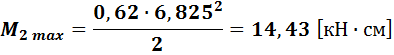
По полученному максимальному изгибающему моменту определяем требуемую величину плиты:
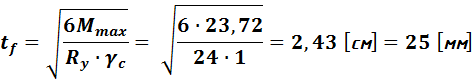
3)Расчет высоты траверс:
Высота траверс определяется по требуемой длине вертикальных сварных швов. Считаем в запас прочности, что усилие на плиту передается только через швы, прикрепляющие ствол колонны к траверсам и не учитываем швы, соединяющие ствол колонны непосредственно с плитой базы. Траверса работает на изгиб, как балка с двумя консолями. Высота траверсы определяется из условия прочности сварного соединения траверсы с колонной. Рассчитаем угловые швы на условный срез.
Требуемую длину сварных швов рассчитываем по двум сечениям шва: по металлу шва и по границе сплавления.
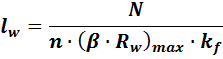
где:
n = 4 (т.к. четыре расчетных вертикальных шва)
βf – коэффициент проплавления (СНиП)
 - расчетное сопротивление металла шва (СНиП)
- расчетное сопротивление металла шва (СНиП)
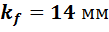 - катетом шва задаемся в зависимости от толщины свариваемых элементов
- катетом шва задаемся в зависимости от толщины свариваемых элементов
Сварные швы будем выполнять полуавтоматической сваркой электродами Э42, выполненными из проволоки сплошного сечения Св-08А со значением 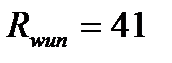 кН/см2. Для стали С255 значение
кН/см2. Для стали С255 значение 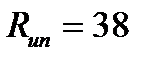 кН/см2. Таким образом, расчетные сопротивления сварного шва по металлу шва и по границе сплавления соответственно будут равны ( по табл.3 СНиП II-23-81*):
кН/см2. Таким образом, расчетные сопротивления сварного шва по металлу шва и по границе сплавления соответственно будут равны ( по табл.3 СНиП II-23-81*):
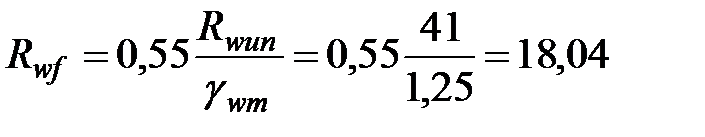
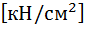
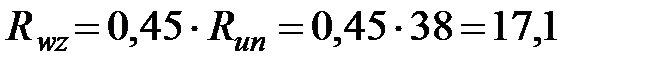
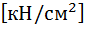
Значения коэффициентов  при сварке в нижнем положении равны:
при сварке в нижнем положении равны:

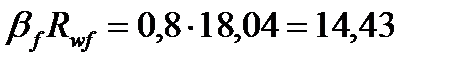
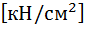
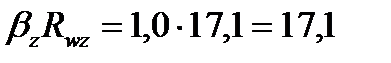
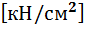
Следовательно, необходимо рассчитать сварной шов на условный срез по металлу границы сплавления.
В сечении по металлу шва:
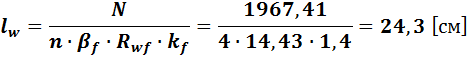
Высота траверс: 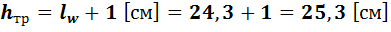 (учитываем возможный непровар швов).
(учитываем возможный непровар швов).
Принимаем 
Дата добавления: 2016-02-20; просмотров: 10936;
