Гиперболической регрессии
| № п.п. | х | у | 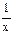
| 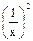
| 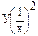
|
| х1 | у1 | 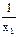
| 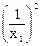
| 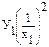
| |
| х2 | у2 | 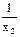
| 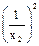
| 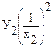
| |
| … | … | … | … | … | … |
| n | хn | уn | 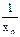
| 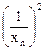
| 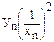
|
| Σ | Σх | Σу | 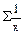
| 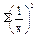
| 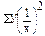
|
В качестве примера можно взять исходные данные, характеризующие зависимость себестоимости 1 кг меда от продуктивности 1 пчелосемьи по 30 сельскохозяйственным организациям. По этим данным необходимо составить и решить уравнение регрессии между указанными признаками.
Себестоимость единицы продукции, представляющая комплекс всех затрат в денежной форме, разделенных на к количество продукции, можно условно расчленить на постоянную и переменную части. При этом постоянная часть расходов не зависит от объема продукции, а переменная – изменяется пропорционально ее количеству. Поэтому изменение себестоимости 1 кг продукции под воздействием продуктивности пчел теоретически можно представить в виде гиперболической регрессии.
Графическое изображение зависимости с помощью координатной диаграммы показало, что основная масса точек сосредоточена в форме, близкой к гиперболической. Поэтому для составления и решения системы нормальных уравнений (9.13), (9.14) гиперболической регрессии целесообразно найти значения 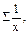 Σу,
Σу, 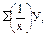
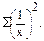 Расчет этих значений приведен в табл. 11.8.
Расчет этих значений приведен в табл. 11.8.
Т а б л и ц а 11.8. Расчет вспомогательных показателей для уравнения
Дата добавления: 2016-02-20; просмотров: 668;
