Сущность, виды и значение уравнений регрессии

Под регрессией понимается функция, предназначенная для описания зависимости изменения результативных признаков под влиянием колебаний признаков-факторов. Понятие регрессии введено в статистическую науку по предложению английского ученого Ф. Гальтона.

В корреляционно-регрессионном методе парной корреляционной взаимосвязи соответствует однофакторная регрессионная модель, множественной взаимосвязи – множественная регрессия. Поэтому наличие корреляционной связи между параметрическими признаками позволяет приближению представить значения результативного признака в виде некоторой функции от величины одного или нескольких факторных признаков.

Функцию, показывающую корреляционную зависимость между признаками, принято называть уравнением регрессии. Если оно связывает лишь два признака, то представляет собой уравнение парной регрессии; если отражает зависимость результативного признака от двух, трех и более факторных признаков – это уравнение множественной регрессии.

Ранее было показано, что при выявлении корреляционной формы, связывающей результативный признак с одним факторным, помогает графическое изображение корреляционной связи в виде поля корреляции. Обычно считают, что увеличение результативного и факторного признаков в арифметической прогрессии при прямой связи требует применения линейной, а при обратной – гиперболической регрессии.

Прямая связь, при которой результативный признак увеличивается в арифметической прогрессии, а факторный повышается быстрее признака-результата, требует применения параболической или показательной регрессии. Уравнение множественной регрессии обычно выражается либо прямой, представляющей собой функцию многих переменных, либо степенной функцией.

Составление уравнения регрессии означает прежде всего определение его параметров, используя для этого, где возможно, способ наименьших квадратов, согласно которому сумма квадратов отклонений фактических значений результативного признака от теоретических значений, рассчитанных по уравнению регрессии, должна быть наименьшей, т.е.

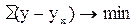(11.7)

где у – фактические варианты признака-результата; у_х – теоретические значения признака-результата.

Это условие приводит к системе нормальных уравнений, решение которых позволяет определить параметры уравнения регрессии. Заметим при этом, что число нормальных уравнений на одно больше числа входящих в уравнение регрессии факторов. Если известны параметры уравнения, то, подставляя в него принятые значения факторных признаков, можно рассчитать теоретическое значение результативного признака, что делает удобным применение корреляционных уравнений при прогнозировании результативных признаков.

Уравнение регрессии может показать связь между признаками более точно, если оно построено на основании достаточно большой статистической совокупности. Но поскольку оно все-таки выражает приближенную меру связи, то уравнение регрессии нередко называют моделью связи между признаками.