б) СА с цифровым трактом последней ПЧ.

– обработка сигналов от входа СА до последнего смесителя совпадает со случаем а);

– после аналогового последнего смесителя и до оцифровки сигнал проходит через (аналоговый) полосовой фильтр с центром на последней ПЧ; этот фильтр, при необходимости, то есть когда частота 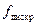отсчетов не достигает двух 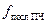и критерий Найквиста не выполняется, выполняет функцию защиты от наложения спектров (элиэйзинга), заодно он отфильтровывает вредные и неинформативные составляющие на выходе смесителя;

– далее сигнал оцифровывается АЦП с частотой 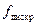отсчетов; все дальнейшие преобразования осуществляются в цифровом формате сигналов;

– следующее преобразование – прохождение сигнала через цифровой фильтр последней ПЧ с устанавливаемой, в широком диапазоне значений, полосой 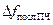, причем время 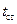«стояния» на очередной точке сетки частот находится в обратной зависимости от ;

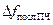– далее выполняется «цифровое детектирование» оцифрованного сигнала: вычисляются «медленно меняющиеся» квадратуры 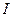и и 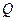каждый отсчет находится как ;

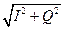– остальные преобразования – те же, что в случае а).

Комбинирование цифровых отсчетов амплитуды

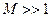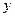Задача комбинирования цифровых отсчетов амплитуды ставится так: на одну отображаемую на экране точку (в дальнейшем интерполированной) кривой приходится цифровых отсчетов амплитуды (блок отсчетов); нужно указать математическое отображение величин в одну величину , которая и будет индицироваться на экране, то есть указать подходящую функцию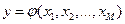 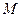переменных.

Но что значит «подходящая»? На языке математической статистики, а точнее, той ее части, которая называется теорией оценок, это задача построения «хорошей» или даже «оптимальной» непараметрической оценки для 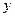по выборочным данным 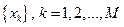. Решение этой задачи сильно зависит от того, что мы знаем (априори, или из предыдущих наблюдений) о структуре выборки 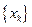, в частности, к какому классу относится входной сигнал. Например, если входной сигнал суть стационарный случайный процесс с порождающим выборку 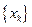белым (или почти белым) спектром мощности, то выборка 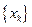– случайна и однородна; оптимальное построение таких выборок хорошо проработано в классической математической статистике. Если входной сигнал относится к тому же классу, но с небелым и приближенно наблюдаемым спектром, то задачу можно свести к предыдущему варианту путем введения весовой функции неоднородности выборки.

Довольно общий случай – входной сигнал в виде смеси стационарного или с известной нестационарностью случайного процесса (например, как проявление шумов разного рода) и детерминированного процесса с резко неоднородным спектром. Сформулировав подходящий критерий оптимальности, можно построить оптимальную оценку, максимизирующую значение этого критерия. Другими словами, теоретическое построение хорошей или оптимальной оценки требует как минимум частотно-временной структурной модели входного сигнала. Практическое применение такого подхода сводится к следующему:

а) Используя опыт и теоретические предпосылки, заранее подбираются несколько спектрально-временных моделей сигналов, могущих появиться на входе СА.

б) Для каждой модели разрабатывается оптимальное правило комбинирования отсчетов и каждое правило закладывается в математическое обеспечение СА.

в) Далее возможны два способа действий:

в1) вырабатывается система индикаторов 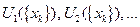(функций выборки 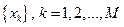) таких, что в зависимости от областей значений, в которые они попадают при наблюденных 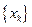, автоматически принимается та или иная модель и реализуется соответствующее правило комбинирования;

в2) оператор предварительно обучается так, чтобы по наблюдаемым на экране (нескомбинированным) отсчетам он мог, более или менее уверенно, назначать подходящую модель и, тем самым, алгоритм комбинирования.

Изложенный подход можно рассматривать как план на будущее; представим теперь подход, реализованный во многих моделях СА. В математическое обеспечение заложено несколько алгоритмов комбинирования отсчетов каждого блока; выбор того или иного алгоритма поручается интуиции тренированного оператора, предварительно наблюдающему последовательность отсчетов на некотором участке спектра.

Прокомментируем некоторые популярные алгоритмы комбинирования.

а) Метод центрального отсчета. Это простейший, интуитивно понятный метод комбинирования: в качестве представителя блока отсчетов берется отсчет, занимающий в блоке центральное по времени положение (если в блоке четное число отсчетов, можно взять или любое из двух центральных отсчетов, или среднее арифметическое от них). Точки, представляющие отдельные блоки отсчетов, можно соединить отрезками прямых или, более сложным образом, с помощью сплайнов. Часто считают [2.6], что этот метод хорош для модели (однородного) случайного процесса, но неудобен для анализа детерминированного узкополосного сигнала.

б) Метод максимального значения. В качестве представителя блока отсчетов берется наибольший из них. Метод дает относительную гарантию того, что отдельные локальные спектральные линии сигнала не останутся незамеченными при индикации; поэтому метод считается одним из самых важных и установлен по умолчанию в ряде СА; однако, считается [2.6], что этот метод недостаточно хорош для анализа случайного процесса.

в) Метод минимального значения. В качестве представителя блока отсчетов берется наименьший из них. Этот метод предусмотрен в большинстве анализаторов, хотя используется гораздо реже метода пикового значения и метода центрального значения. Считается [2.6], что этот метод хорош в некоторых процедурах идентификации сигналов, а также для отделения гармонических сигналов от импульсных, что, например, необходимо производить в тестах на электромагнитную совместимость.

г) Метод нормального комбинирования. Чтобы объединить положительные свойства методов центрального отсчета и пикового значения, во многих СА предлагается метод нормального комбинирования, привлекающий информацию о росте или падении отсчетов в пределах блока. Если отсчеты в рамках одного блока и падал, и рос, и это повторялось в ряде других блоков, то оценки чередуются: для первого блока берется оценка максимального значения, для второго – минимального значения, для третьего – снова максимального значения и т.д. Если же на протяжении нескольких блоков отсчеты будут только расти или только падать, то метод нормального детектирования будет работать как метод максимального значения. Идея метода в том, что если встретится спектральная линия шириной в несколько блоков отсчетов, то она не будет пропущена, если же на входе СА действует случайный процесс, то его специфика будет хорошо отображена. Применение этого метода может привести к сдвигу максимума спектральной кривой на экране вправо на одну точку; в некоторых моделях СА этот эффект компенсируется, в других – игнорируется.

д) Метод среднего. Для тех, кто имеет опыт использования терминологии, методов и рекомендаций математической статистики, наиболее естественной оценкой отображаемого значения 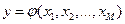по выборке 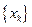является среднее арифметическое выборочных значений:

.

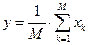Если выборка 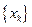чисто случайна (выборочные значения – реализации независимых случайных величин) и стационарна, то такая оценка эффективна в смысле Фишера, то есть состоятельна, несмещенна и имеет минимальную дисперсию. В то же время, например, оценки центрального отсчета, максимального отсчета и минимального отсчета имеют большую дисперсию, чем оценка среднего, что объясняется просто: первая вообще не учитывает остальные отсчеты, вторая и третья – учитывают их слабо.

Приведенная оценка усредняет значения отсчетов спектральных амплитуд. Логически к ней примыкает оценка, усредняющая квадраты амплитуд, то есть значения отсчетов спектральной плотности мощности:

,

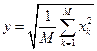и оценка, усредняющая логарифмы амплитуд:

,

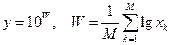которые могут показаться более естественными при интерпретации результатов анализа в терминах спектральной плотности мощности или децибелов. При аналоговой обработке методу среднего соответствует пропускание видеосигнала через фильтр нижних частот или интегратор.

Фильтрация в ПЧ и сглаживание индицируемого спектра

Даже в целом детерминированный входной сигнал имеет некоторую (аддитивную) случайную составляющую, относительный уровень которой можно оценить параметром, называемым отношением сигнал-шум. По мере прохождения сигнала по тракту к его случайной составляющей прибавляются собственные (внутренние) шумы аппаратуры и отношение сигнал-шум уменьшается; это уменьшение оценивается параметром, называемым коэффициентом шума. В результате, на выходе последнего смесителя СА мощность сигнала есть сумма мощностей детерминированной части и случайной части. Каждая из этих частей имеет свой спектр мощности. Обычно спектр детерминированной части локализован в некоторой конечной полосе, в то время как спектр случайной части размыт в очень широкой полосе, ограниченной только фильтрующим действием преселектора и предыдущих каскадов преобразования частоты. Поскольку мы рассматриваем СА последовательного анализа с дискретной частотной перестройкой, то при установленной полосе 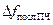фильтра последнего ПЧ спектр детерминированной части не искажается, а лишь просматривается с некоторым разрешением, в то время как мощность случайной части уменьшается в тем большей степени, чем уже полоса 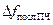. В результате, отношение сигнал-шум на выходе фильтра много больше отношения на выходе последнего смесителя. Этот эффект есть ничто иное, как усреднение, он обязан уменьшению относительной дисперсии при сложении некоррелированных случайных значений и может быть строго математически описан.

Из сказанного не следует, что нужно во всех случаях устанавливать как можно меньшее значение 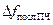, получая выигрыш в отношении сигнал-шум и в разрешающей способности. Дело в том, что с уменьшением 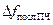резко увеличивается время частотной развертки, а это не только снижает оперативность измерений, но и надолго разносит по времени наблюдение разных участков спектра сигнала; последнее важно, если сигнал имеет конечное время существования или/и нестационарный спектр, меняющийся с некоторой скоростью. Действительно, пусть выбраны анализируемый интервал частот (установкой значений 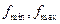) и величина 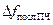. Для обеспечения нужной точности спектрального анализа необходимо, чтобы время «стояния» последнего гетеродина на одной частотной точке 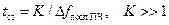было достаточно большим, а число частотных точек в развертке будет 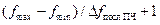; в результате время частотной развертки обратно пропорционально квадрату 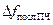и может оказаться недопустимо большим.

Рассмотрим пример. Пусть частотный диапазон анализа СА составляет от 10 МГц до 10 ГГц ( 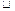10 ГГц); выберем для анализа всего 1% диапазона: 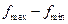=100 МГц. Установим 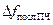=10 Гц, примем 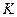=10, тогда 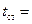1 с. Время развертки составит 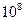с, или 2780 часов (!), что абсолютно неприемлемо. Если же при тех же параметрах установить 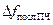=10 кГц, то время развертки составит 10 с.

Обратимся теперь к манипуляциям с цифровыми отсчетами амплитуды, получаемыми после детектирования (аналогового или цифрового). Приведенное выше среднее

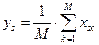
от отсчетов 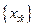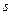- го блока есть вид сглаживания видеоданных; если же среднее захватывает несколько ( 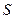) блоков, то получается более сильное сглаживание, чем при комбинировании отсчетов блока:

.

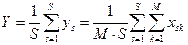Природа сглаживания отличается от природы фильтрации (усреднения) в тракте ПЧ и состоит в следующем. Спектр как функция частоты, который отображался бы при отсутствии сглаживания (при условии соединения точек на экране отрезками прямых) имеет колебания разных частотных масштабов; если частотный аргумент заменить на временной, то этот исходный спектр станет функцией времени, от которой можно взять преобразование Фурье. В результате получится функция частоты, которую можно назвать «спектром спектра» или «вторым спектром». Осуществляя сглаживание, мы усредняем (убираем) наиболее высокочастотные колебания второго спектра. Чем больше параметр 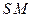сглаживания, тем левее (размытая) граница удаленных частот второго спектра; в результате отображаемая кривая (первого) спектра становится все глаже, откуда и название операции. Подытоживая, можно сказать, что усиливая фильтрацию в тракте ПЧ (обужая фильтр ПЧ) мы отслеживаем спектр сигнала все с большим разрешением (расплачиваясь, правда, за это увеличением длительности развертки), а усиливая сглаживание (увеличивая параметр 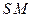), мы делаем кривую индицируемого спектра более гладкой, расплачиваясь обеднением «второго спектра» за счет его высоких частот.

Процесс сглаживания дает повод ввести еще одно понятие спектрального разрешения (разрешающей способности), совершенно отличное от ранее рассмотренного классического. Если последнее определялось полосой разрешения, то есть спектральным расстоянием между двумя спектральными линиями, при котором они разрешены, то новое разрешение определяется числом отсчетов АЦП, идентифицируемое как одна точка на экране, или соответствующая этому числу полоса. Этот вид разрешения можно назвать разрешением индикации, а соответствующую полосу – полосой разрешения индикации. Чем больше эта полоса, тем хуже разрешение индикации, но более гладкая, «красивая» отображаемая кривая спектра.

Межкадровое усреднение

Цифровое управление дисплеем (цифровой дисплей) дает возможность осуществления другого вида сглаживания, называемого межкадровым усреднением. Здесь усреднение проводится поточечно, за две или более частотные развертки. Удобно находить межкадровое среднее рекуррентно, по мере прохождения все новых разверток, по схеме:

,

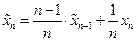где 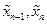– средние после 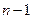-ой и после 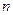-ой разверток соответственно;

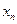– отсчет на 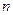-ой развертки.

Такой алгоритм придает процессу наглядность: картина на дисплее в каждой частотной точке постепенно сходится к среднему за установленное число проходов. Эта установка задает степень усреднения, так же как при обычном видео-усреднении, которое теперь можно назвать трассовым, степень усреднения задается параметром .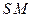

Межкадровое усреднение, также как и трассовое, сглаживает индицируемую кривую спектра, расплачиваясь примерно таким же временем. Однако результаты межкадрового и трассового усреднений могут быть разными, например, в модели сигнала с нестационарным (меняющимся во времени) спектром. Поэтому важно, что эти два вида усреднения можно совместить в одном эксперименте. Установим число 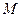отсчетов в блоке, число 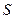блоков в трассовом усреднении, число 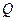разверток в межкадровом усреднении. Тогда индицируемое значение в одной частотной точке равно

.

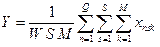Оптимальный выбор величин 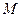, , 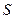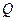позволяет адекватно учесть особенности модели сигнала.

Временное стробирование

Как указывалось выше, недостатком представления сигналов в частотной области на базе преобразования Фурье является отсутствие временной локализации в последнем. В то же время, сам метод последовательного спектрального анализа приводит к тому, что различные участки индицируемого спектра относятся к различным временным интервалам существования сигнала, но это никак не проявляется при наблюдении кривой спектра на экране. Кроме того, в практике радиотехнических систем СВЧ, особенно в беспроводных систем связи, часто используются сигналы, занимающие перекрывающие, или даже совпадающие области частотного спектра, но разделенные во временной области. Перечисленные факторы подталкивают к идее осуществлять, помимо спектрального анализа, еще и управление наблюдением сигналов по времени. Одним из простейших механизмов такого управления является временное стробирование. Оно использует внешний управляющий сигнал, активизирующий те или иные функции СА на определенных интервалах времени (стробах), и закрывающий эти функции на других на других интервалах времени (антистробах).

Временное стробирование позволяет раздельно наблюдать спектры сигналов, разделенных по времени. Эта функция полезна, например, при наблюдении неоднородной радио-импульсной последовательности, сигналов с временным мультиплексированием, сигналов в системе многостанционного доступа с временным разделением каналов (TDMA), перемежающихся или уплотненных импульсных сигналов, модулируемых всплеском сигналов.

Выполняемые при этом операции можно условно разделить на следующие:

– измерение спектральных характеристик разделенных по времени сигналов;

– измерение спектра сигнала в одной временной ячейке системы TDMA;

– отделение и наблюдение спектра неинформативных временных частей сигналов, например, переходных процессов периодической последовательности импульсов.

Из всех возможных объектов стробирования СА наиболее часто используются два:

– выход видеодетектора; сигнал отключается в антистробах от дальнейшего тракта, применяется пиковый режим комбинирования, время развертки устанавливается так, чтобы строб действовал хотя бы один раз на каждую отображаемую точку дисплея;

– последний гетеродин; во время антистроба гетеродин не переключается на новые частоты и дисплей отображает одну точку спектра.

Преимущества цифровой обработки

Начиная с 80-х годов прошлого века СА испытали значительные изменения, в основном за счет быстрого наступления цифровой обработки сигналов. Это стало возможным благодаря прогрессу в высокопроизводительных АЦП. Цифровые технологии обработки сигналов позволили улучшить все показатели эффективности СА: скорость, точность, разрешение и т.д. Наиболее сильные улучшения стали результатом освоения полностью цифровой секции ПЧ. Цифровая секция последней ПЧ обеспечивает целый букет преимуществ для пользователя. Ключевым преимуществом, доставляемым цифровыми разрешающими фильтрами последней ПЧ, является резко возросшая разрешающая способность СА, обязанная недостижимой для аналоговых фильтров полосовой избирательности цифровых фильтров, например, 4:1 на уровнях -60 дБ, -3 дБ. Наибыстрейшие измерения возможны при комбинации БПФ-анализа (при отсутствии частотной развертки) – для узких полос обзора, и последовательного анализа с частотной разверткой – для широких полос обзора. Дальнейшие преимущества высокой надежности, стереотипности исполнения, удешевления реализации и др. принесли разработка, производство и применение двух интегральных схем: ИС преобразований от вычислений квадратур 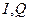до преддисплейной комбинаторики, и ИС RISC-процессора («интегральная микросхема с сокращенным набором»), осуществляющая дальнейшие преобразования до дисплея.

В современных СА с высоким весом цифровой обработки имеется возможность повысить точность и разрешение установки частоты, и без того очень высокой. Для этого в тракте последнего ПЧ предусмотрен счетчик частоты. Он подсчитывает количество пересечений нуля сигналом в этом тракте за конечный интервал времени, например, за 0.1 с, и пересчитывает результат в текущее отклонение от номинальной частоты. Само это отклонение обусловлено двумя составляющими: флуктуациями частоты гетеродинов за счет фазовых шумов и флуктуациями мгновенной частоты сигнала за счет его зашумленности. Поскольку гетеродины СА выполнены как высоко частотно-стабильные синтезаторы (особенно первый гетеродин, стабилизированный кварцевым генератором), первую составляющую частотного отклонения можно сделать достаточно малой, и на первый план выходит составляющая, обусловленная зашумленностью анализируемого сигнала. Таким образом, появляется дополнительная функция СА – измерение частоты. Благодаря фазовым ухищрениям, дополняющим счет пересечений нуля, можно достичь разрешения частоты в десятки миллигерц на периоде 0.1 с.

Подытожим достижения СА, ставшие возможными благодаря высокой степени «цифровизации»:

– возможно усреднение с регулируемой постоянной времени как напряжения, так и мощности и логарифма мощности;

– возможно трассовое, межкадровое, а также смешанное сглаживание;

– возможен счет частоты с высоким разрешением;

– хранящиеся в памяти данные можно извлекать как в линейном, так и в логарифическом масштабе;

– превосходный коэффициент прямоугольности цифровых фильтров обеспечивает уникальное частотное разрешение анализа, почти идеальное для последовательного анализа;

– коэффициент 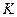, связывающий необходимое время «стояния» 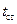на одной частоте последнего гетеродина с полосой разрешения 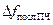( 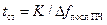) в случае цифрового исполнения разрешающего фильтра может быть значительно меньше, чем при аналоговом исполнении;

– возможность легкого исполнения комбинирования по методу среднего;

– цифровое исполнение всех разрешающих фильтров последней ПЧ позволяет создать уникальный набор устанавливаемых полос разрешения (например, 160 различных полос), удовлетворяющий потребности любого пользователя;

– возможно включить, в зависимости от полосы обзора, режим последовательного анализа или режим БПФ;

–присутствующий на схеме рис. 2.3.1 логарифмический усилитель до сих пор никак не комментировался; при полностью цифровом тракте последней ПЧ и этот усилитель – также цифровой; его точность (точность выполнения им функции логарифмирования) значительно выше, чем при аналоговом исполнении;

– точность установки каждой полосы разрешения намного выше, чем при аналоговых разрешающих фильтрах; за счет этого, в частности, выше точность измерения спектральной амплитуды, спектральной плотности мощности и мощности в канале;

– разброс пропусканий в максимуме разрешающих цифровых фильтров меньше, чем при аналоговом исполнении; это в частности, облегчает калибровку прибора;

– при отсутствии в тракте последнего ПЧ аналоговых звеньев усиления, зависящих от опорного уровня, не существует неопределенности «усиления тракта последней ПЧ»;

– возможно изменять настройки СА без существенного влияния на точность измерения;

– итоговое влияние отмеченных улучшений таково, что СА с полностью цифровым трактом последней ПЧ имеет значительно лучшую точность спектрального анализа, чем СА с аналоговым трактом.

Эффективность спектроанализатора

Как и для анализаторов цепей, для СА пока не сформулирован комплексный критерий эффективности. На этом этапе изложения мы не будем углубляться в предложенные частные критерии эффективности, а перечислим и поясним некоторые количественные факторы, отражающие свойства АЦ и входящие в комплексный и некоторые частные критерии.

1. Точностные характеристики СА. Выше уже было дано общее понятие о комплексе параметров и характеристик, группирующихся вокруг понятия «точность измерения» и характеризующих степень приближения результатов измерений к истинным значениям измеряемых величин: погрешность измерения (погрешность прибора) и факторы, ее обусловливающие; разновидности числового представления погрешности: абсолютные, относительные, приведенные; систематические, случайные погрешности и промахи, и факторы, их обусловливающие, а также понятия измерительной и производственной калибровке. Там же указано на роль теории оценок как раздела математической статистики. Также как при анализе цепей, при анализе сигналов в общем случае объектами измерения являются комплекснозначные функции частоты и времени, например, (комплексный) спектр сигнала или (действительная) частота сигнала в тракте последнего ПЧ. Было показано, почему абсолютная и относительная комплексные ошибки не годятся для практического использования. Поэтому и в случае спектрального анализа сигналов мы приходим к двум системам измеряемых величин и их ошибок; первая система: амплитудные спектры и спектры мощности, то есть действительные неотрицательные функции частоты, а также они же в децибельной мере, и абсолютные и относительные ошибки этих функций; вторая система: фазовые спектры и их абсолютные ошибки. Существуют два популярных подхода к интерпретации случайных ошибок амплитудного и фазового спектров: в виде доверительного интервала при фиксированной доверительной вероятности и в виде среднеквадратичной ошибки; и два популярных подхода к интерпретации систематических ошибок амплитудного и фазового спектров: в виде интервала неопределенности между возможными минимальным и максимальным значениями и в рамках квазистатистического подхода.

Не вдаваясь в собственно анализ точностных характеристик тех или иных измеряемых величин СА, назовем факторы неопределенности, порождающие парциальные неопределенности, то есть вклады в общую неопределенность измерения. Основные факторы:

– рассогласования СВЧ-секций: выхода источника сигнала и входа СА; выхода радиочастотного тракта и входа смесителя и т.д.;

– неопределенность, вносимая радиочастотным аттенюатором;

– неопределенность, вносимая частотной неравномерностью входного фильтра и преселектора;

– неопределенность, вносимая частотной неравномерностью смесителей и гетеродинов;

– неопределенность опорного уровня за счет неопределенности усилений трактов;

– неопределенность, вносимая разрешающими фильтрами;

– неопределенность масштаба отображения экрана;

– остаточная неопределенность после измерительной калибровки.

Неопределенность, вносимая рассогласованиями, возникает из-за переотражений от стыков разных импедансов; адекватным аппаратом для учета возникающих при этом парциальных волн и, соответственно, вычисления возникающей ошибки, являются потоковые сигнальные графы.

Неопределенность, вносимая радиочастотным аттенюатором, состоит из дух частей: неопределенности ослаблений при различных положениях аттенюатора на разных частотах и вклада в общую частотную характеристику СА, особенно в ее высокочастотной части.

Неопределенность, вносимая частотной неравномерностью входного фильтра и преселектора различна на разных частотах. В нижнем поддиапазоне СА используется фиксированный ФНЧ, в верхнем – перестраиваемый полосовой фильтр, преселектор. У ФНЧ неравномерность АЧХ мала и близка к расчетной, поэтому вносимая им неопределенность также мала. Преселектор, обычно выполненный на управляемом ЖИГ-резонаторе, имеет значительные неравномерности АЧХ и потому вносит значительную неопределенность. Эта неопределенность может быть существенно снижена с помощью внешних достаточно точных генератора монохроматического сигнала и измерителя мощности: Последовательно, на нескольких интересующих нас частотах сигнал подается на СА и измеритель мощности и их показания сравниваются.

Неопределенность, вносимая частотной неравномерностью смесителей и гетеродинов – объект сложного анализа, из-за использования гармонического смешения, следующего отсюда разбиения диапазона СА на гармонические полосы и т.д.

Неопределенность опорного уровня за счет неопределенности усилений трактов обязана, в основном, тракту последней ПЧ. Если этот тракт выполнен как аналоговый, то его усилитель и аттенюатор настроены так, чтобы скомпенсировать изменения в установках радиочастотного аттенюатора и потери преобразования последнего смесителя, так что амплитуды входного сигнала соотносятся с верхней отметкой координатной сетки дисплеи, то есть опорным уровнем. Усилитель и аттенюатор последней ПЧ работают на одной частоте, поэтому не вносят вклада в неопределенность частотной характеристики, однако дают вклад в амплитудную неопределенность, обусловленный неточностью итоговой настройки, который и называется неопределенностью опорного уровня. Однако, при полностью цифровой последней ПЧ аналогового усилителя в этом тракте нет, поэтому неопределенность опорного уровня отсутствует.

– Неопределенность, вносимая разрешающими фильтрами, обусловлена тем, что у аналоговых разрешающих фильтров с разной полосой вносимые потери различны, особенно если это фильтры разного типа, например, 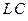-фильтры, применяемые при широких полосах разрешения, и кварцевые фильтры, применяемые при узких полосах разрешения. В результате образуется неопределенность переключения полос разрешения. Однако, в полностью цифровом тракте последней ПЧ условия возникновения названной неопределенности другие. Во-первых, разрешающие фильтры для всех полос разрешения исполнены как цифровые, часто в рамках специализированной интегральной схемы. Хотя эти фильтры не идеальны, они отличаются высокой повторяемостью, вдобавок, применяется некоторый алгоритм компенсации, уменьшающий ошибку повторяемости. Поэтому вклад цифровых фильтров в неопределенность переключения полос разрешения достаточно мал. Во-вторых, кроме аналогового фильтра, препятствующего наложению спектров, иногда [2.6] перед оцифровкой в тракте последней ПЧ ставят аналоговый предварительный фильтр с переключаемой полосой, в 2.5 раз шире соответствующей полосы цифрового фильтра разрешения. У этого фильтра при каждой включенной его полосе имеются неопределенности центральной частоты, полосы пропускания и коэффициента ослабления, которые и определяют вклад в неопределенность переключения полос пропускания.

– Неопределенность масштаба отображения экрана в аналоговом тракте последней ПЧ возникает из-за того, что усиление усилителя тракта в логарифмическом масштабе амплитуды неидеально аппроксимирует логарифмическую кривую, а в линейном масштабе – не идеально линейна. В обоих режимах любое отклонение от идеальной характеристики дает вклад в неопределенность амплитуды (мощности). Этот тип неопределенности называется достоверностью масштаба отображения. Цифровой тракт последней ПЧ не включает аналоговый усилитель; функция логарифмирования (как и линейная функция) осуществляется математически почти идеально (то есть с пренебрежимой ошибкой); поэтому в традиционном смысле неопределенности масштаба отображения в этом случае нет. Однако, сама эта неопределенность имеет место по другим причинам. Во-первых, в отсутствие усилителя последней ПЧ на поверхность выходит маленькая неопределенность амплитуды за счет сжатия усиления в радиочастотной секция, заметная уже при мощности входного сигнала СА выше -20 дБм. Во-вторых, еще одним источником неопределенности амплитуды является неточность реализованного расположения диапазона усиления АЦП по отношению к модельному расположению. В-третьих, вклад в неопределенность масштаба отображения дает специфическая для цифровой техники ошибка квантования, обусловленная тем, что оцифровка – это процесс дискретизации аналогового сигнала по времени и квантования по уровню.

Заметим, что в данном случае нас интересует вызываемая шумом квантования нелинейность средней характеристики АЦП. Поэтому вклад в рассматриваемую неопределенность можно уменьшить классическим приемом, представляющим собой вид рандомизации данных: добавлением шумовой (некоррелированной) цифровой последовательности (подмешивающий сигнал или дифер, dither). Это подмешивание изменяет структуру шума квантования: сглаживает среднюю характеристику АЦП, делая ее более линейной, но, естественно, увеличивает средний уровень шума квантования. Если до подмешивания отношение (сигнал/шум квантования) достаточно велико (например, больше 10 дБ), то можно считать, что выигрыш в линейности средней характеристики АЦП более важен, чем проигрыш в точности единичного отсчета сигнала (то есть до усреднения); если же это отношение недостаточно велико, то названный проигрыш не окупается выигрышем. Поэтому производители СА с подмешиванием оставляют пользователю возможность выключить его при значительной зашумленности оцифрованного сигнала до усреднения.

– Остаточная неопределенность после измерительной калибровки это многокомпонентная неопределенность, оставшаяся после измерительной калибровки из-за неидеальности последней. Все СА используют встроенный или внешний прецизионный генератор, обеспечивающий монохроматический сигнал заданной частоты, используемый как опорный сигнал для абсолютной калибровки СА. В процессе последней СА переносит абсолютную калибровку опорного сигнала на другие частоты и амплитуды. Из-за неточностей амплитуды и частоты опорного сигнала, в частности, обусловленных частотной (фазовой) нестабильностью его генератора, образуется неопределенность измерения этих величин СА, обычно малая на частоте опорного сигнала и увеличивающаяся при отклонении от этой частоты. Например, во многих СА фирмы Аджилент (США) используется встроенный калибратор на частоте 50 МГц и на этой частоте абсолютная ошибка измерения амплитуды спектроанализатором, заявленная в спецификациях для PSA-серии СА: 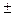0.24 дБ, но значительно больше на частотах в несколько ГГц. Если у СА есть встроенный калибратор, то ничто не мешает при случае использовать более точный или более близкий к интересующим нас частотам внешний калибратор.

– Точности измерения спектральной амплитуды (спектральной плотности мощности) и мощности сигнала. Представленные абсолютными и относительными, систематическими (в форме максимальных значений или квазислучайных параметров) и случайными ошибками, эти точности зависят, в общем случае, от установок СА (разрешающая полоса, степень усреднения, степень сглаживания и т.д.), от истинных значений измеряемых величин, формы их представления (линейная, логарифмическая), от степени зашумленности сигнала. Представляющие ошибки аккумулируют вклады всех неопределенностей (перечисленных выше и других). Отдельная точностная характеристика – амплитудная (мощностная) ошибка маркера, устанавливаемого на кривую спектра для получения информации об абсолютных значениях спектральной амплитуды и частоты. Эта точность, кроме прочего, зависит от точности наведения маркера на кривую, в свою очередь, наибольшей при наведении на экстремум кривой.

– Точность измерения частоты. Формально, судя по названию прибора – СА, измерение частоты – побочная (хотя и важная) функция прибора. С помощью СА можно проводить два вида измерений частоты: абсолютное и относительное. Абсолютные измерения проводятся с целью определить или проверить частоту конкретного сигнала, а также для анализа нежелательных сигналов. Например, для проверки, что радиостанция работает на предписанной ей частоте, или при исследовании некоторой паразитной помехи. Относительные измерения частоты полезны для выяснения частотного расстояния между двумя конкретными сигналами, для определения частоты модуляции и т.д.

Переход гетеродинов СА на высокостабильные синтезаторы частоты (в основном – косвенного синтеза, то есть с использованием опорных кварцевых генераторов), произошедший еще в 80-е годы 20-го века, резко повысил точность ее измерения. Дальнейший существенный прогресс в точности был связан с применением усовершенствованных счетчиков пересечений уровня. Большое значение для точности измерения частоты имеет короткопериодная (фазовый шум) и длиннопериодная (дрейф и температурные уходы) стабильности частоты гетеродинов, наличие или отсутствие встроенного опорного генератора частоты, период между частотными калибровками и подстройками, наличие или отсутствие трассируемого лабораторного стандарта частоты, время непрерывной работы и т.д. Точность относительных измерений частоты зависит, в частности, от точности полосы обзора, определяемой неопределенностью отображения на дисплее частотных расстояний между спектральными компонентами.

Частотная точность маркера зависит от частотной калибровки дисплея, выбранного количества дисплейных точек, усреднений и сглаживаний, точности наведения маркера на кривую. Последняя, как и амплитудная точность, максимальна при наведении на экстремум. Чтобы добиться хорошего результата, полезно сузить полосу обзора и полосу разрешения и тем самым визуально сузить отображаемый пик кривой, на который наводится маркер.

У многих СА есть специальный режим маркера, в котором действуют схемы внутренних счетчиков, предназначенных для устранения влияния полосы обзора и полосы разрешения на частотную точность маркера. Важно, что в этом случае счетчик считает не пересечения входного сигнала СА, а пересечения сигнала в тракте последней ПЧ. Кроме того, чтобы отклонения частот гетеродинов от номинальных не увеличивали ошибку измерения частоты, счетчики в режиме маркера считают и пересечения гетеродинных сигналов. Процессор обрабатывает эту информацию и вычисляет частоту входного сигнала. Чтобы в режиме маркера устранить шум как фактор ошибки, стараются, по крайней мере в этом режиме, добиться достаточно большого отношения сигнал-шум, или хотя бы наводить маркер на точки, достаточно далекие от индицируемого уровня шума. При счете пересечений простым счетчиком неустранимо влияние на точность измерения частоты параметра, называемого разрешением счетчика и задаваемого наименьшим значимым разрядом в представлении результата счета. Влияние разрешения счета удваивается при пользовании дельта-маркерами, то есть парами маркеров для визуализации частотных разностей.

2. Статические диапазоны измерений. Зададимся вопросом: в каком диапазоне может быть измерена величина, определяемая СА, в «медленном» режиме, то есть при последовательном изменении установок, например, разрешающих полос фильтра последней ПЧ, положений входного аттенюатора и т.п. Такой диапазон можно назвать статическим (иногда [2.6] его называют диапазоном измерения). Ответы на этот вопрос не определены, если не принять, что диапазон измерений величины это область значений измеряемой величины, в пределах которой нормированы погрешности средства измерений. То есть для каждой измеряемой величины мы задаемся некоторой максимальной допустимой ошибкой и находим диапазон измерения этой величины, в пределах которого ошибка измерения не больше заданной.

С помощью скалярного СА можно измерять спектральную амплитуду (спектральную плотность мощности) как функцию частоты, мощность всего сигнала (среднюю мощность случайного процесса как сигнала), мощность сигнала в спектральном канале, «мгновенную» частоту сигнала (здесь мы, как и прежде, не касаемся таких дополнительных функций СА, как измерения коэффициента шума цепи, фазовых шумов, быстрых и медленных частотных (фазовых) нестабильностей генераторов и т.п.).

а) Статические диапазоны измерения мощности, средней мощности, спектральной амплитуды (спектральной плотности мощности) при заданных предельных погрешностях этих величин ограничены сверху сжатием первого смесителя и сжатием усиления усилителей при минимальном ослаблении управляемых аттенюаторов, а снизу – уровнем шума при минимальной доступной в данном измерении полосе разрешающего фильтра ПЧ (не всегда равной полосе самого узкого фильтра ПЧ).

б) Статический диапазон измерения частоты сигнала сильно зависит от того, применяется ли техника счета пересечений нуля, какова допустимая ошибка измерения частоты (в «досчетчиковую» эру допустимая ошибка в гигагерцовом диапазоне составляла несколько МГц!), каков временной интервал измерения и т.д. В итоге, статический диапазон измерения частоты не обязательно равен частотному диапазону СА (см. ниже).

Нужно отличать статический диапазон измерения величины от динамического диапазона.

3. Динамический диапазон амплитудных измерений. Несмотря на лексическую схожесть терминов, динамический диапазон принципиально отличается от статического по смыслу и по назначению. Если статический диапазон есть просто диапазон измеряемых величин с использованием возможностей перестроек параметров СА, то динамический диапазон понимается как возможность одновременно измерять два или более сигнала разной величины. Точнее, величина динамического диапазона это отношение, выраженное в дБ, наибольшего и наименьшего сигналов, которые могут одновременно измеряться СА с заданной степенью (относительной) точности (упоминание точности почти всегда относится к меньшему сигналу, т.к. больший сигнал измеряется с большей относительной точностью).

Ситуация с одновременным измерением нескольких сигналов разной величины возникает во многих случаях. Например, при наблюдении двух или более тестовых спектральных компонент, при измерении гармонических искажений или интермодуляций и т.д. Динамический диапазон, в отличие от статического, относится к измерениям при фиксированном наборе установок СА, без их изменения. Динамический диапазон не единствен: он зависит почти от каждой из установок и поэтому различен при разных их наборах. В соответствии с общим принципом, чтобы сделать понятие диапазона определенным, необходимо задать максимальную допустимую ошибку измерения соответствующей величины. Поскольку динамический диапазон современных СА очень велик (например, 100 или более дБ) допустимо для удобства анализировать его величину как разность (в дБ) максимально достижимой верхней границы и минимально достижимой нижней границы (хотя разработаны графические методы одновременного анализа всего диапазона).

Во всех источниках и руководствах по СА указано, что снизу динамический диапазон амплитудных измерений ограничен а) шумами, б) нелинейными искажениями, вносимыми смесителем (в основном гармоническими искажениями второго и третьего порядков и интермодуляциями третьего порядка). Но математическая трактовка этого тезиса в части а) зачастую утрируется, размыта неопределенными понятиями, осложнена ненужными и даже неверными предположениями и т.д. Например, предлагается в качестве нижней границы диапазона брать индицируемый в области предполагаемого отсутствия сигнала уровень шума (который, кстати, обозначают неопределенными терминами типа «средний шум» и т.п.); или предлагается считать нижней границей уровень, отстоящий на определенное число дБ от этого «уровня шума», называя это число «отношением сигнал-шум», не связывая выбор этого отношения с предположениями о статистической структуре шума и классе сигналов; или, наоборот, делая мало обоснованные предположения о распределении вероятностей «уровня шума», связывают «отношение сигнал-шум» с относительной ошибкой измерения и считают, что нижняя граница диапазона обусловлена максимальной допустимой ошибкой измерения и т.д. и т.п.

Конечно, эти нечеткости, неопределенности, нестрогости трактовки не имеют большого значения, если нас удовлетворит знание динамического диапазона с точностью до нескольких дБ, например, нам подходит ответ: «динамический диапазон данного СА при таких-то установках – порядка 100-106 дБ». Но если динамический диапазон – критический параметр для данного применения СА, если от этого вопроса зависит приобретение данного СА, если «идет борьба за каждый дБ», то необходима более определенная, более четкая, более строгая трактовка этого вопроса на базе теории случайных процессов. Здесь мы ограничимся тезисами качественного характера о части а) нижней границы динамического диапазона:

– из внешних соображений должна быть задана максимальная допустимая ошибка измерения на нижней границе диапазона;

– должны быть четко ограничены классы потенциальных сигналов и помех (флуктуаций, шумов, в том числе фазовых шумов и т.д.), то есть конкретизирована математическая модель сигналов и помех;

– должно быть сформулировано строгое количественное понятие отношения сигнал-шум, пригодное в рамках данной модели сигналов и помех;

– это отношение, с одной стороны, должно быть связано с ошибкой измерения, с другой – с устанавливаемыми параметрами СА;

– в результате, нижняя граница диапазона в части а) должна быть представлена как функция установок СА и структур сигналов и помех.

Что касается части б) тезиса, то традиционно ставится и решается задача определения оптимального режима первого смесителя, в частности, оптимально уровня входного сигнала смесителя; в качестве условия оптимальности берется равенство неопределенности за счет шума и ошибки за счет нелинейных искажений, или другое условие.

Верхняя граница динамического диапазона ограничена допустимыми искажениями всякого рода (сжатие усилений, сжатие смесителей и т.д.), перегрузками и т.п.

Существует еще одно практически полезное диапазонное понятие, которое часто путают с динамическим диапазоном: дисплейный диапазон. Это калиброванный амплитудный диапазон дисплея СА. Например, дисплей с десятью делениями с калибровкой 10 дБ на деление, очевидно, имеет дисплейный диапазон 100 дБ. Сказанное в полной мере относится к СА с цифровой секцией последней ПЧ, или с аналоговой секцией – при использовании узких разрешающих фильтров, которые делаются цифровыми. Однако дисплеи СА с полностью аналоговой секцией последней ПЧ обычно калибруются лишь на 85-90 дБ вниз от опорного уровня. В этом случае нижняя часть дисплея обозначает область диапазона от -85 или -90 дБ до 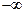дБ относительно опорного уровня. Возникают вопросы: а) можно ли в полной мере использовать дисплейный диапазон; б) может ли динамический диапазон превзойти дисплейный диапазон. На первый вопрос ответ положительный всегда, на второй – положительный для некоторых моделей СА. В последнем случае путем увеличения усиления тракта последней ПЧ малые сигналы переводятся на калиброванную область дисплея, а большие – выше опорного уровня. Хорошо, если при этом точность отображения сигналов не ухудшается, как это имеет место для СА серии PSA фирмы Аджилент.

4. Чувствительность СА. В технике вообще (не только радиотехнической) термин «чувствительность» используется в разных смыслах. Мы можем различать три понятия, связанных с этим термином.

а) Преобразовательная чувствительность. Так предлагается назвать параметр, который обычно называется просто чувствительностью, то есть способность реагировать на изменения входного сигнала; она оценивается отношением изменения выходного сигнала к вызвавшему его изменению входного сигнала. Например, чувствительность отклонения луча осциллографа измеряется в миллиметрах на вольт.

б) Обнаружительная чувствительность СА. Это способность обнаруживать с достаточной уверенностью (например, с достаточной вероятностью при заданной вероятности «ложной тревоги») малые сигналы или малые изменения спектра зафиксированного сигнала. Возможна постановка и решение этой задачи на базе статистической теории обнаружения как частной задачи испытания статистических гипотез.

в) Пороговая чувствительность СА: оценивается минимальной абсолютной мощностью входного сигнала СА, спектр которого, при заданном спектральном разрешении, может быть измерен СА с заданной степенью точности. По-существу, эту чувствительность можно понимать как пересчитанную на входную абсолютную мощность нижнюю границу динамического диапазона. Пороговая чувствительность зависит не только от установок СА, но и характера (класса) сигнала и структуры внутреннего шума СА.

1. Частотный диапазон СА может быть представлен в двух вариантах:

а) как общий диапазон, внутри которого могут размещаться поддиапазоны спектрального анализа до какой-то ширины каждый; например, некий СА имеет общий диапазон от 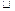0 до 50 ГГц, внутри которого может быть произвольно размещен поддиапазон анализа шириной до 1 ГГц; такой частотный диапазон можно назвать статическим;

б) как максимальный поддиапазон спектрального анализа; такой частотный диапазон можно назвать максимальной глубиной частотной панорамы.

Нужно иметь в виду, что хотя подавляющее большинство СА сконструированы как универсальные приборы, с весьма широким классом анализируемых сигналов и неограниченным спектром приложений, в настоящее время может быть вполне оправданным создание более дешевого, быстродействующего, удобного, мобильного и т.д. специализированного СА с узким классом сигналов и/или узким спектром приложений; например, для изучения (поверки) структуры сигналов беспроводной связи, или для обнаружения газовых выделений по их спектрам излучения. Поэтому вариант а) вполне возможен.

6. Диапазон и дробность разрешающих способностей СА. Как показано выше, разрешающая способность СА задается полосой разрешения, равной

,

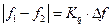где 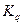– коэффициент, зависящий от того, аналоговый или цифровой разрешающий фильтр, и если аналоговый, то от его порядка; для аналогового фильтра 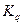– порядка нескольких единиц, для цифрового – несколько больше единицы; 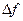– полоса разрешающего фильтра.

Таким образом, в конечном счете, разрешающая способность СА задается полосой разрешающего фильтра 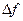. Когда-то разрешающие фильтры были аналоговыми, затем узкополосные из них стали выполняться цифровыми, а остальные – аналоговыми; наконец, в настоящее время все разрешающие фильтры принято выполнять цифровыми. Это привело к тому, что как фактор эффективности разрешающая способность представлена диапазоном полос разрешения и дробностью (количеством) их значений. Фактически и то, и другое ограничено лишь здравым смыслом. Минимальное значение 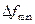разрешающей полосы ограничено тем, что для получения одного отсчета требуется время 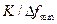, где 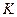– порядка единиц. Обычно берут 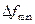порядка 1 Гц, при меньших полосах сеанс измерения будет длиться недопустимо долго. Максимальное значение 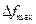ограничено тем, что должно выполняться условие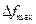 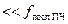. В результате, при значении последней ПЧ порядка нескольких десятков МГц отношение 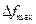/ 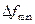составляет не более 7 декад. При 10 разрешающих фильтрах на декаду получается всего порядка 70 фильтров, при 20 фильтров на декаду – порядка 140 фильтров. Эти фантастические возможности выбора разрешения – одно из преимуществ использования цифровых технологий.

7. Оперативность (быстродействие). Это важный фактор эффективности СА; от оперативности зависит сама применимость данной модели СА в ряде приложений, например, при настройке и тестировании радиотехнических устройств на поточной производственной линии, при анализе сигналов ограниченного времени действия, при выполнении функций обнаружения. Кроме того, оперативность часто является фактором производительности СА. Для измерительного прибора быстродействие характеризуется интервалом времени, необходимого для производства единичного измерения, в качестве которого в данном случае нужно понимать получение спектра сигнала в заданном частотном диапазоне с необходимым качеством, возможно, в течение нескольких проходов частотного диапазона. Принципиальная часть этого времени – время измерения, включающее время переходов с одной частотной точки на другую, время «стояния» на частотных точках, время переключения кадров(предполагается, что процессы записи, расчетов и индикации не удлиняют этого времени). Полезно различать быстродействие собственно измерений, быстродействие с учетом калибровки, быстродействие с учетом калибровки и подготовительных процедур. Например, чтобы СА вышел на стандартный режим теплового тренда, может понадобиться несколько десятков минут [2.6]; это часть времени подготовительных процедур; альтернатива – постоянно включенное питание.

8. Стабильность отражает постоянство во времени метрологических показателей средства измерений. Часто эта характеристика представляется обратной величиной – нестабильностью показателей во времени. Общая нестабильность СА складывается из нестабильности (в частности, частотной) гетеродинов, переключателей, разъемов и т.д.

9. Помехозащищенность и электромагнитная совместимость. Электромагнитная совместимость средства измерения определяется гарантией достаточно низкого уровня его влияния на окружающие электромагнитные устройства, обеспечивающей сохранение свойств последних. Поскольку СА – пассивное устройство, а единственными его активными элементами являются гетеродины, требования нормативных документов по электромагнитной совместимости легко выполнить.

Помехозащищенность – способность электронного средства измерений сохранять в процессе измерений свои характеристики при наличии внешних радиопомех. Применительно к СА требования к помехозащищенности определяются нормативными документами; выполнимость этих требований зависит от состава, расположения и характеристик окружающих устройств; с другой стороны, влияние внешних радиопомех выражается характеристиками точности, обнаружения, динамического диапазона измерения полезных сигналов под влиянием этих помех.

1. Надежность. Общие комментарии к этому фактору эффективности даны выше.

11. Вес и габариты. Эти факторы не требуют комментариев.

12. Рабочие условия (условия измерений). Общие комментарии к этому фактору эффективности даны выше.

13. Поколения СА. Общие соображения о поколениях радиотехнических средств измерения изложены выше. Что касается СА, то большинство современных моделей этого прибора можно отнести к четвертому поколению: они имеют автоматическое управление от встроенного или внешнего компьютера; используют микросхемы и микросборки большой степени интеграции, многослойные печатные платы; используют цифровые технологии обработки сигналов после детектора огибающей или даже после последнего смесителя.

Можно ожидать, что для пятого поколения СА будет характерна полная готовность средств измерения к объединению в измерительные системы, с межкомпьютерной трансляцией данных и результатов, автоматическим формированием, выдачей и распечаткой отчетов с широким выбором номенклатуры и форматов, хранение установленных параметров, данных и результатов измерений в выбираемых номенклатурах и форматах и т. д.; а также переход к цифровой обработке не позднее тракта второй ПЧ; векторный характер спектрального анализа; возможность анализа в отличных от Фурье базисах, в частности, вейвлет-анализа.