Апріорної невизначеності
3.1 Основні положення статистичної теорії прийняття рішень
Розглянемо спрощену дихотомічну (двохальтернативну) модель прийняття рішень. Нехай на вході СПР (рис. 3.1.1а), яка функціонує за умов дії на неї випадкового фактора f(t), роздільно у часі відбуваються дві події А1і А2. За основну приймемо гіпотезу 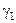 про наявність на вході події А1, а за альтернативну – гіпотезу
про наявність на вході події А1, а за альтернативну – гіпотезу 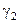 про наявність на вході події А2. Множина випадкових векторів
про наявність на вході події А2. Множина випадкових векторів 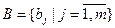 на виході системи утворює підмножину простору допустимих рішень – розбиття
на виході системи утворює підмножину простору допустимих рішень – розбиття 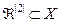 , яке поділяється роздільною гіперповерхнею на області класу
, яке поділяється роздільною гіперповерхнею на області класу 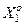 і класу
і класу 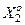 (рис. 3.1.16).
(рис. 3.1.16).
 | |||
 | |||
а) б)
Рисунок 3.1.1– Дихотомічна модель прийняття рішень:
а) інформаційна модель СПР; б) розбиття простору
допустимих рішень на два класи
Побудова оптимальної в інформаційному сенсі роздільної гіперповерхні між областями 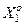 і
і 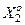 , що забезпечує максимальну достовірність рішення, є центральною задачею статистичної теорії прийняття рішень, а алгоритм прийняття рішень тоді полягає в порівнянні деякого порогового (критичного) значення відношення правдоподібності
, що забезпечує максимальну достовірність рішення, є центральною задачею статистичної теорії прийняття рішень, а алгоритм прийняття рішень тоді полягає в порівнянні деякого порогового (критичного) значення відношення правдоподібності 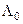 із здобутою статистичною оцінкою
із здобутою статистичною оцінкою 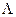 . При цьому, якщо
. При цьому, якщо 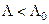 , то основна гіпотеза
, то основна гіпотеза 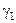 приймається, інакше - відкидається.
приймається, інакше - відкидається.
Якщо для двохальтернативного рішення відомі ймовірності 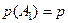 і
і 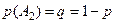 , тоді можна використовувати критерій максимума правдоподібності, який дозволяє мінімізувати повну ймовірність помилкового рішення:
, тоді можна використовувати критерій максимума правдоподібності, який дозволяє мінімізувати повну ймовірність помилкового рішення:
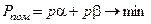 , (3.1.1)
, (3.1.1)
де 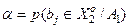 – помилка першого роду;
– помилка першого роду;
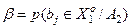 – помилка другого роду.
– помилка другого роду.
З урахуванням, що 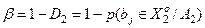 , де
, де 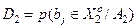 – друга достовірність, перетворимо вираз (3.1.1) до вигляду
– друга достовірність, перетворимо вираз (3.1.1) до вигляду
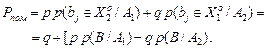 (3.1.2)
(3.1.2)
Необхідною умовою мінімізації Рпом є від’ємність виразу в квадратних дужках в (3.1.2). Звідки маємо відношення правдоподібності:
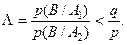 (3.1.3)
(3.1.3)
Таким чином, за критичне значення критерію максимума правдоподібності слід прийняти 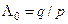 .
.
У випадку, коли 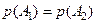 , тобто мають місце найбільш важкі в статистичному сенсі умови прийняття рішень, використовують критерій ідеального спостерігача, для якого згідно з (3.1.3)
, тобто мають місце найбільш важкі в статистичному сенсі умови прийняття рішень, використовують критерій ідеального спостерігача, для якого згідно з (3.1.3) 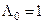 і рішення приймається за алгоритмом: якщо
і рішення приймається за алгоритмом: якщо 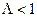 , то приймається гіпотеза
, то приймається гіпотеза 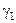 , інакше – гіпотеза
, інакше – гіпотеза 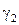 .
.
На практиці широке застосування знайшов статистичний критерій Неймана-Пірсона, який дозволяє мінімізувати вираз (3.1.1) при заданих обмеженнях на одну із помилок. Звичайно приймається 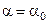 . Тоді як поріг класифікації приймається величина
. Тоді як поріг класифікації приймається величина 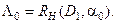
3.2. Мінімізація залишкової невизначеності за
статистичними критеріями
Залишкова невизначеність після прийняття рішень характеризується умовною ентропією, яка в статистичній теорії прийняття рішень подається у вигляді функції [10]
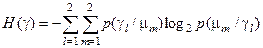 , (3.2.1)
, (3.2.1)
де 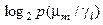 – логарифмічна функція втрат.
– логарифмічна функція втрат.
Відомо, що ймовірність прийняття гіпотези 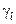 за умови
за умови 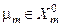 дорівнює
дорівнює 
p( 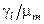 )=
)= 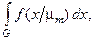 (3.2.2)
(3.2.2)
де 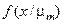 – умовна функція щільності розподілу ймовірностей.
– умовна функція щільності розподілу ймовірностей.
Функція (3.2.2) обчислюється як результат інтегрування функції щільності розподілу ймовірностей по області 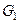 , якщо
, якщо 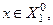 і - по області
і - по області 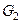 , якщо
, якщо 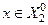 . Ймовірність p(
. Ймовірність p( 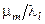 ) визначається як
) визначається як
p( 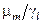 )=
)= 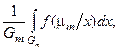 (3.2.3)
(3.2.3)
де 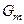 – обсяг, що відповідає області класу
– обсяг, що відповідає області класу 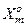 .
.
Після підстановки (3.2.2) і (3.2.3) у вираз (3.2.1) обчислимо його похідну по змінній роздільної гіперповерхні та прирівняємо її нулю:
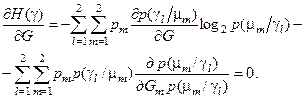
Прийнявши до уваги, що загальний обсяг 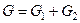 є незмінним, тобто
є незмінним, тобто 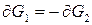 , після ряду перетворень отримаємо:
, після ряду перетворень отримаємо:
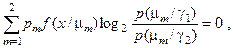
що дає відношення правдоподібності :
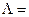
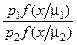 =
= 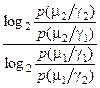 . (3.2.4)
. (3.2.4)
Для вибору порогу розпізнавання 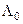 за критерієм Неймана-Пірсона у праці [10] за формулою (3.2.4) побудовано номограму, наведену на рис. 3.2.1. Тут криві однакових рівнів відповідають значенням критерію
за критерієм Неймана-Пірсона у праці [10] за формулою (3.2.4) побудовано номограму, наведену на рис. 3.2.1. Тут криві однакових рівнів відповідають значенням критерію 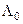 при різних значеннях першої достовірності
при різних значеннях першої достовірності 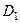 та помилки першого роду
та помилки першого роду 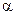 при
при 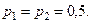
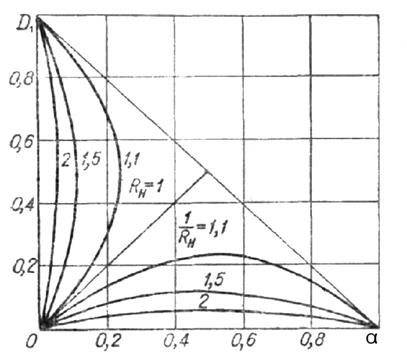
Рисунок 3.2.1– Номограма для обчислення порогу
розпізнавання за критерієм Неймана-Пірсона
Оскільки при 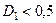 функція (3.2.1) не належить робочій області свого визначення, то значення критерію
функція (3.2.1) не належить робочій області свого визначення, то значення критерію 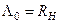 визначаються тільки за кривими, що знаходяться в області номограми вище прямої
визначаються тільки за кривими, що знаходяться в області номограми вище прямої 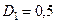 . Для цього необхідно задати на вісі абсцис допустиме (прийнятне) значення помилки першого роду
. Для цього необхідно задати на вісі абсцис допустиме (прийнятне) значення помилки першого роду 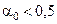 і відновити з нього перпендикуляр. За порогове можна вибирати будь-яке значення, яке перетинає перпендикуляр при
і відновити з нього перпендикуляр. За порогове можна вибирати будь-яке значення, яке перетинає перпендикуляр при 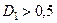 . При цьому необхідно враховувати, що менше значення порогу розпізнавання гарантує більшу достовірність, але забезпечує меншу надійність (завадозахищеність) прийняття рішень. Знайдене за номограмою значення критерію Неймана-Пірсона
. При цьому необхідно враховувати, що менше значення порогу розпізнавання гарантує більшу достовірність, але забезпечує меншу надійність (завадозахищеність) прийняття рішень. Знайдене за номограмою значення критерію Неймана-Пірсона 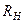 мінімізує залишкову невизначеність (3.2.1).
мінімізує залишкову невизначеність (3.2.1).
3.3. Детерміновані теоретико-ігрові моделі прийняття рішень
Розглянемо задачу вибору із скінченої множини допустимих рішень 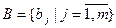 рішення (стратегії)
рішення (стратегії) 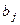 , яка дозволяє за можливих умов (станів природи)
, яка дозволяє за можливих умов (станів природи) 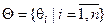 отримати гарантований виграш. Така модель прийняття рішень у теорії ігор характеризується таблицею платежів (табл. 3.3.1)
отримати гарантований виграш. Така модель прийняття рішень у теорії ігор характеризується таблицею платежів (табл. 3.3.1)
Таблиця 3.3.1– Таблиця платежів
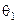
| 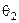
| ... | 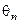
| |
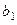
| 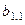
| 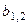
| ... | 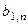
|
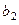
| 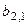
| 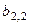
| ... | 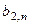
|
| ... | ... | ... | ... | ... |
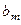
| 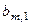
| 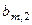
| ... | 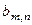
|
Величина 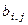 характеризує в теорії ігор платіж і звичайно задається евристично.
характеризує в теорії ігор платіж і звичайно задається евристично.
У випадку відсутності інформації про стан природи має місце детермінована задача прийняття рішень за умов невизначеності. Для її розв’язання існують такі три основні підходи за відповідними критеріями.
Критерій максиміну. Нехай 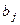 – найгірший результат, який дорівнює
– найгірший результат, який дорівнює 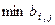 . Знайдемо стратегію за якою величина
. Знайдемо стратегію за якою величина 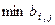 є максимальною, тобто
є максимальною, тобто
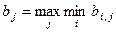 . (3.3.1)
. (3.3.1)
У цьому випадку виграш називаеться максиміном, який забезпечує гарантований прибуток за будь-яких станів природи.
Критерій мінімакса або втрачених можливостей.Цей критерій мінімізує програш у результаті втрачених можливостей. Тому поміняв місцями max і min у виразі (3.4.1) отримаємо критерій мінімакса:
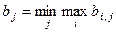 . (3.3.2)
. (3.3.2)
Таким чином, мінімакс забезпечує мінімальний програш за будь-яких станів природи. Для його обчислення формується платіжна матриця – матриця втрачених можливостей, значення елементів якої є оберненими до значень відповідних елементів матриці виграшів.
Критерій рівноможливих станів природи.Цей критерій як оптимальну визначає таку стратегію, для якої сума виграшів є максимальною, тобто
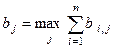 . (3.3.3)
. (3.3.3)
Приклад 3.3.1 [14].Нехай задано матрицю виграшів (табл. 3.3.2).
Таблиця 3.3.2 – Матриця виграшів
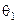
| 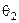
| |
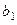
| 1 | 11 |
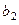
| 10 | 6 |
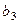
| 0 | 14 |
На практиці стратегії 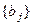 можуть бути різними режимами технологічного процесу при виготовленні деякого продукту, а елементи множини
можуть бути різними режимами технологічного процесу при виготовленні деякого продукту, а елементи множини 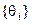 характеризують зовнішні фактори, які впливають на ефективність виробництва (якість і вартість сировини, енергоносіїв, кліматичні умови та інше).
характеризують зовнішні фактори, які впливають на ефективність виробництва (якість і вартість сировини, енергоносіїв, кліматичні умови та інше).
Знайдемо оптимальну стратегію за максимінним критерієм (3.3.1):
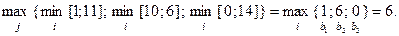
Таким чином, можна зробити висновок, що максимінною стратегією є 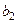 .
.
Для визначення мінімаксної стратегії сформуємо із урахуванням табл. 3.3.2 матрицю втрачених можливостей (табл. 3.3.3).
Таблиця 3.3.3 – Матриця втрачених можливостей
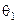
| 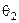
| |
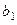
| ||
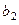
| ||
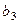
|
Для табл. 3.3.3 за критерієм (3.3.2) знайдемо мінімаксну стратегію:
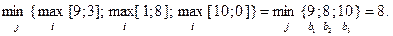
Таким чином, за мінімаксним критерієм оптимальною так само є стратегія 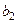 .
.
Нарешті, для табл. 3.3.2 знайдемо оптимальну стратегію за критерієм рівноможливих станів природи (3.3.3):
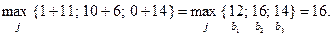
Бачимо, що стратегія 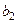 є оптимальною за всіма основними критеріями теорії ігор.
є оптимальною за всіма основними критеріями теорії ігор.
3.4. Прийняття рішень за умов ризику
При прийнятті рішень за умов ризику доцільно використовувати статистичну модель. Нехай відомі ймовірності 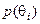 , які задовільняють умові повноти подій:
, які задовільняють умові повноти подій:
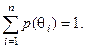
На практиці для обчислення оцінок імовірностей 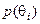 необхідна наявність повторних вибірок, отриманих із генеральної сокупності значень випадкової величини. За цієї умови можна сформувати платіжну матрицю у вигляді табл 3.4.1.
необхідна наявність повторних вибірок, отриманих із генеральної сокупності значень випадкової величини. За цієї умови можна сформувати платіжну матрицю у вигляді табл 3.4.1.
Таблиця 3.4.1–Таблиця платежів
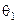
| 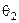
| ... | 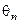
| |
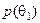
| 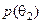
| ... | 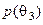
| |
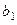
| 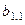
| 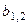
| ... | 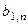
|
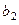
| 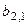
| 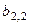
| ... | 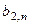
|
| ... | ... | ... | ... | ... |
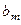
| 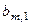
| 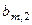
| ... | 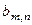
|
Алгоритм визначення оптимальної стратегії полягає в знаходженні взважених сум виграшів для всіх станів природи. Як розв’язок вибирають ту стратегію 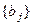 , для якої сума максимальна, тобто
, для якої сума максимальна, тобто
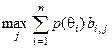 . (3.4.1)
. (3.4.1)
Приклад 3.4.1. Нехай відомі ймовірності 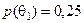 і
і 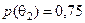 . Тоді отримаємо табл. 3.4.2.
. Тоді отримаємо табл. 3.4.2.
Таблиця 3.4.2 – Матриця виграшів
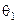
| 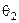
| |
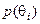
| 0,25 | 0,75 |
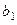
| ||
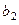
| ||
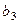
|
За формулою (3.4.1) маємо:
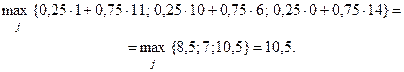
Таким чином, краще всього використовувати стратегію 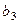 .
.
Для дослідження впливу значень ймовірності 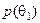 на вибір оптимальної стратегії позначимо її через змінну p. На рис. 3.4.1 показано області вибору оптимальної стратегії залежно від значень ймовірності р, які відкладаються на вісі абсцис від нуля до одиниці. Оскільки має місце
на вибір оптимальної стратегії позначимо її через змінну p. На рис. 3.4.1 показано області вибору оптимальної стратегії залежно від значень ймовірності р, які відкладаються на вісі абсцис від нуля до одиниці. Оскільки має місце 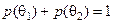 , то на лівій вісі ординат відкладено згідно з табл. 3.5.2 виграші для фактора
, то на лівій вісі ординат відкладено згідно з табл. 3.5.2 виграші для фактора 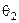 (
( 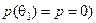 , а на правій вісі-для фактора
, а на правій вісі-для фактора 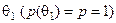 .
.
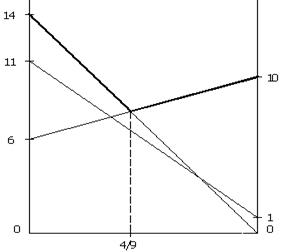 |
Рисунок 3.4.1– Області вибору оптимальних стратегій
Як показано на рис. 3.4.1, при 0 < p < 1/9 краще використовувати стратегію 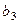 , а при 4/9 < p < 1 – стратегію
, а при 4/9 < p < 1 – стратегію 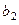 . При p=4/9 однаково, яку із стратегій
. При p=4/9 однаково, яку із стратегій 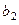 або
або 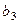 використовувати. Стратегію
використовувати. Стратегію 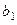 ні при яких значеннях ймовірності p застосовувати недоцільно.
ні при яких значеннях ймовірності p застосовувати недоцільно.
3.5 Вибір оптимальних змішаних стратегій за умов
неповної невизначеності. Байесівський підхід
Знайдемо середній виграш для кажної допустимої стратегії Sl за теоремою про повну ймовірність:
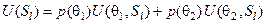 . (3.5.1)
. (3.5.1)
Стратегія, для якої функцяя U(Sl), що визначається за формулою (3.5.1), є максимальною, називаеться байесівською.
Розглянемо випадок, коли ОПР отримує деяку апріорну інформацію шляхом проведення експерименту без урахування вартості його проведення. У цьому випадку збільшення гарантованого виграшу досягається використанням не однієї стратегії, а декількох, які називаються змішаною стратегією.
Приклад 3.5.1 [14]. Для отримання гарантованої середньої корисності від запланованих турпоходів турист перед кожним турпоходом дзвонить у бюро погоди, отримуючи прогностичну інформацію. У найпростішому випадку турист повинен вибрати одну з таких альтернативних стратегій: b1 – одягнутися стосовно до теплої погоди; b2 – одягнутися стосовно до холодної погоди.
Як експерт по проведенню багатоденних турпоходів турист складає матрицю виграшів (табл. 3.5.1), де q1 – тепла погода і q2 – холодна погода
Таблиця 3.5.1– Матриця виграшів
| q1 | q2 | |
| b1 | ||
| b2 |
За критерієм максиміну перевага віддається стратегії 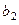 : max{min[10;0]; min{4,7}; min [0;4]}= 4. Легко перевірити, що за іншими критеріями стратегія
: max{min[10;0]; min{4,7}; min [0;4]}= 4. Легко перевірити, що за іншими критеріями стратегія 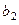 так само є оптимальною. Таким чином, турист при виборі стратегії b2 за критерієм максимину отримує 4 у. о. «корисності».
так само є оптимальною. Таким чином, турист при виборі стратегії b2 за критерієм максимину отримує 4 у. о. «корисності».
Тепер ускладнемо задачу. Нехай турист отримує одну із трьох відповідей: z1 – очікується тепла погода; z2 – очікується холодна погода; z3 – прогноз невизначений. При цьому за накопиченими статистичними даними відомі ймовірності кожної з відповідей для двох станів природи (табл. 3.5.2)
Таблица 3.5.2– Імовірності станів природи
| z1 | z2 | z3 | |
| q1 | 0,6 | 0,2 | 0,2 |
| q2 | 0,3 | 0,5 | 0,2 |
Тоді задача формулюється так: яку із двох стратегій b1 або b2 слід вибрати залежно від одного з трьох результатів експерименту. У цьому випадку маємо 23 змішані стратегії, які наведено в таблиці 3.5.3.
Таблиця 3.5.3– Матриця змішаних стратегій
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | |
| z1 | b1 | b1 | b1 | b1 | b2 | b2 | b2 | b2 |
| z2 | b1 | b1 | b2 | b2 | b1 | b1 | b2 | b2 |
| z3 | b1 | b2 | b1 | b2 | b1 | b2 | b1 | b2 |
Тут стратегія S1 є легковажною, оскільки незалежно від результату експерименту турист одягається як для теплої погоди. Стратегія S2 – песимістична, оскільки незалежно від результату експерименту турист одягається як для холодної погоди.
Прийнятними вважаються стратегії S3 і S4.
Для формування таблиці корисностей обчислемо за даними табл. 3.5.1 і 3.5.2 для кожної із стратегій {Sl } і двох станів природи взважені суми корисностей U(q1,Sl) і U(q2,Sl):

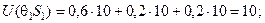
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
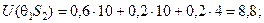
 - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - - -

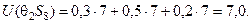
У результаті отримаємо матрицю виграшів (табл. 3.5.4)
Таблиця 3.5.4 – Матриця виграшів

| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | |
| q1 | 10,0 | 8,8 | 8,8 | 7,6 | 6,4 | 6,2 | 5,2 | 4,0 |
| q2 | 1,4 | 3,5 | 4,9 | 2,1 | 3,5 | 5,6 | 7,0 |
Виключемо з табл. 3.5.4 “погані” стратегії S2 , S5 і S6, які мають середні виграші меньше ніж за іншими стратегіями. Тоді замість табл. 3.5.4 отримаємо табл. 3.5.5, в якій стратегії, що залишилися, називаються допустимими.
Таблиця 3.5.5– Матриця виграшів
| S1 | S3 | S4 | S7 | S8 | |
| q1 | 8,8 | 7,6 | 5,2 | ||
| q2 | 3,5 | 4,9 | 5,6 |
З табл. 3.5.5 видно, що стратегія S7=(b2, b2, b1) є максимінною, за якою треба одягнутися тепло, якщо прогнозується тепла або холодна погода, и легко, якщо прогноз невизначений. Ця стратегія гарантує середню корисність у 5,2 у. о. на один турпохід. Для порівняння нагадаємо, що стратегія b2 гарантує середню корисність тільки у 4 у. о.
Таким чином, використання змішаної стратегії при отриманні додаткової інформації збільшує величину виграшу.
3.6. Метод Белмана за умов невизначеності
Застосування методу Беллмана для розв’язання багатокрокових задач прийняття рішень за умов невизначеності розглянемо на конкретному прикладі.
Приклад 3.6.1[15].Торгівельна фірма повинна прийняти рішення про закупівлю партії товару у зовнішнього виробника з наступною перепродажею товару 
 на протязі року в своїх торгівельних точках. Таким чином, умови прийняття рішення, в основному, характеризуються невизначеністю майбутнього попиту на цей товар, який може з часом змінюватися. За умовами контракту додаткову закупівлю товару фірма може здійснити лише через чотири місяці після початку календарного року. Таким чином, необхідно забезпечити правильне рішення як при початковій закупівлі, так і при можливій додатковій закупівлі товару з метою забезпечення максимального очікуваного прибутку. Щомісячний торгівельний прибуток, що може отримати фірма в кожній із можливих ситуацій, наведено в табл. 3.6.1.
на протязі року в своїх торгівельних точках. Таким чином, умови прийняття рішення, в основному, характеризуються невизначеністю майбутнього попиту на цей товар, який може з часом змінюватися. За умовами контракту додаткову закупівлю товару фірма може здійснити лише через чотири місяці після початку календарного року. Таким чином, необхідно забезпечити правильне рішення як при початковій закупівлі, так і при можливій додатковій закупівлі товару з метою забезпечення максимального очікуваного прибутку. Щомісячний торгівельний прибуток, що може отримати фірма в кожній із можливих ситуацій, наведено в табл. 3.6.1.
Таблица 3.6.1 – Прибуток, що одержується при різних
| z1 (високий попит) | z2 (низький попит) | |
| х1 (мала партия) | ||
| х2 (велика партия) |
рівнях попиту
У даному модельному прикладі прогнозується, що сумарний торгівельний щомісячний прибуток від продажу докупленого через чотири місяці товару буде декілька менше, ніж при початковій закупівлі великої партії, і складатиме 180 у. о. в місяць при високому попиті і 40 у. о. – при низькому попиті. Витрати на закупівлю великої та малої партії товару відповідно складають 1000 і 200 у.о., а витрати на можливу додаткову закупівлю товару (через чотири місяці) дорівнюють 840 у. о. Попередні маркетингові дослідження показали, що ймовірність високого попиту на даний товар дорівнює 0,75, а низького – 0,25. Треба рекомендувати керівництву торгівельної фірми таке вирішення проблеми, щоб забезпечити максимальний очікуваний через рік прибуток. За умов апріорної невизначеності мова може тут йти тільки про максимізацію математичного сподівання обсягу прибутку, що очікується. Якщо ситуація з торгівельною фірмою є унікальною (одиничною), тоді доцільно для формування рішення реалізовувати принцип гарантованого результату на базі максимінного критерію, що в будь-якому випадку корисно на першій стадії дослідження з метою попередньої оцінки потенційних можливостей.  Подамо сформовану задачу у вигляді дерева рішень (рис. 3.6.1). Тут квадратиками зображено розв’язуючі вершини, а кружечками – допоміжні вершини, що характеризують невизначений стан середовища. Позначення
Подамо сформовану задачу у вигляді дерева рішень (рис. 3.6.1). Тут квадратиками зображено розв’язуючі вершини, а кружечками – допоміжні вершини, що характеризують невизначений стан середовища. Позначення 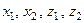 відповідають табл. 3.6.1, а змінні yt означають таке:
відповідають табл. 3.6.1, а змінні yt означають таке: 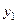 – рішення про додаткову закупівлю товару через чотирі місяці;
– рішення про додаткову закупівлю товару через чотирі місяці; 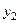 – рішення про відмову від додаткової закупівлі.
– рішення про відмову від додаткової закупівлі.
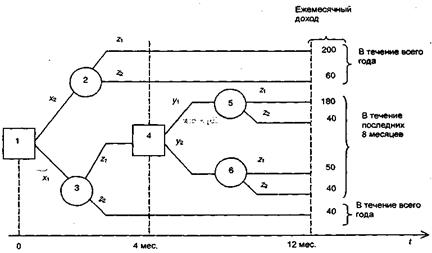
Рисунок 3.6.1 – Дерево рішень
Розв’язання задачі здійснимо за методом Беллмана шляхом просуванням по розв’язуючим вершинам графа справа-наліво. Таким чином, спочатку обробляється розв’язуюча вершина 4 (рис. 3.6.2).

Рисунок 3.6.2– Обчислення прибутку, що очікується, для
вершини 4
Із отриманих двох чисол 380 є найбільшим (максимізується прибуток). Цим числом відмічається вершина 4, а стрілка співпадає з напрямком 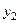 (рис. 3.6.3).
(рис. 3.6.3).

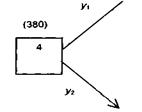
Рисунок 3.6.3– Вибір напрямку руху з вершини 4
Далі переходимо до вершини 1 (рис.3.6.4). Основний висновок полягає в тому, що за критерієм математичного сподівання доцільно з вершини 1 йти в напрямку 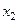 , тобто купувати велику партію товару. При цьому прибуток, що очікується, дорівнює 980 у.о. в рік.
, тобто купувати велику партію товару. При цьому прибуток, що очікується, дорівнює 980 у.о. в рік.

Рисунок 3.6.4–Обчислення прибутку, що очікується, для
вершини 1
При обробленні вершини 4 формується матриця рішень (табл. 3.6.2), де: 600=180*8-840; -520=40*8-840; 400=50*8; 320=40*8. Сама матриця рішень є матрицею платежів (у ній представлено сумарний прибуток за останні вісім місяців).
Таблица 3.6.2 – Матриця рішень для вершини 4
| Y | Z | |
| z1 (0, 75) | z2 (0,25) | |
| y1 y2 | -520 |


У вершині 1 маємо матрицю рішень (платежів), представлену у вигляді табл. 3.7.3, де: 380 = 50 * 4 + 380 - 200;
280 = 40*12-200; 1400 = 200*2-1000; -280 = 60*12-1000.
| X | Z |
| z1 (0, 75) | z2(0,25) | |
| x1 x2 | -280 |
Таблиця 3.6.3– Матриця рішень для вершини 1
Розв’яжемо тепер ту саму задачу, використовуючи принцип гарантованого результату. У вершині 4 так само маємо матрицю виграшів, представлену в табл. 3.6.2. За критерієм максиміну підсумовуємо, що оптимальним є рішення 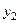 , оскільки найгірший можливий результат при цьому дорівнює 320 у. о. прибутку, а при виборі
, оскільки найгірший можливий результат при цьому дорівнює 320 у. о. прибутку, а при виборі 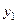 можемо отримати збитки в розмірі 520 у. о. З вершиною 4 тепер асоціюється число 320, а стрілка піде в напрямку
можемо отримати збитки в розмірі 520 у. о. З вершиною 4 тепер асоціюється число 320, а стрілка піде в напрямку 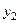 . Далі переходимо до вершини 1 з матрицею із табл. 3.6.4, яка вже відрізняється від матриці із табл. 3.6.3, оскільки тут: 320 = 50 * 4 + 320 - 200.
. Далі переходимо до вершини 1 з матрицею із табл. 3.6.4, яка вже відрізняється від матриці із табл. 3.6.3, оскільки тут: 320 = 50 * 4 + 320 - 200.
Таблиця 3.6.4 –Матриця рішень для вершини 1 у випадку
| X | Z |
| z1 | z2 | |
| x1 x2 | -380 |
гарантованого результату
За критерієм гарантованого результату кращей виявляється альтернатива 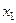 з гарантованим прибутком в 280 у.о. в рік, тобто спочатку рекомендуеться закуплять малу партію товару. Якщо на початку року встановиться високий попит на товар (і продовжиться чотирі місяці), то ми опинимось в розвязуючій вершині 4 и отримаємо прибуток в 50*4+320-200=320 у. о. за рік. При цьому через чотирі місяці згідно з принципом гарантованого результату рекомендуеться не робити додаткових закупок товару (рішення
з гарантованим прибутком в 280 у.о. в рік, тобто спочатку рекомендуеться закуплять малу партію товару. Якщо на початку року встановиться високий попит на товар (і продовжиться чотирі місяці), то ми опинимось в розвязуючій вершині 4 и отримаємо прибуток в 50*4+320-200=320 у. о. за рік. При цьому через чотирі місяці згідно з принципом гарантованого результату рекомендуеться не робити додаткових закупок товару (рішення 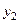 є оптимальним у вершині 4).
є оптимальним у вершині 4).
Таким чином, за умови невизначеності на різних етапах багатокрокової процедури прийняття рішень метод Беллмана дозволяє знаходити оптимальні стратегії поведінки в будь-якій розв’язуючій вершині, тобто для будь-якого стану, в якому може опинитися реальна система.
3.7. Марківські моделі прийняття рішень
Розглянемо багатокрокову задачу прийняття рішень із скінченим числом станів 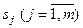 системи
системи 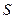 , що оптимізується. Розуміється, що в дискретні моменти часу
, що оптимізується. Розуміється, що в дискретні моменти часу 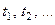 система переходить у новий стан відповідно з деякою матрицею перехідних імовірностей:
система переходить у новий стан відповідно з деякою матрицею перехідних імовірностей:
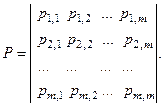
Елемент 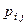 матриці означає ймовірність переходу системи із стану
матриці означає ймовірність переходу системи із стану 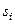 в стан
в стан 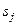 . Таким чином, строки матриці відповідають "старим", а стовпчики – "новим" станам системи. Зрозуміло, що сума елементів будь-якої строки матриці дорівнює 1. Такий процес поведінки системи називаеться марківським.
. Таким чином, строки матриці відповідають "старим", а стовпчики – "новим" станам системи. Зрозуміло, що сума елементів будь-якої строки матриці дорівнює 1. Такий процес поведінки системи називаеться марківським.
Визначення 3.7.1. Процес називається марківським, якщо ймовірність переходу системи в будь-який можливий стан в кожний момент 
 часу визначається тільки її станом в попередній момент часу і не залежить від більш ранньої передісторії.
часу визначається тільки її станом в попередній момент часу і не залежить від більш ранньої передісторії.
Розглянемо конкретний приклад ситуації, коли вона може бути описана за допомогою апарату марківських моделей.
Приклад 3.7.1[15].Деяка фірма займається розробкою програмного забезпечення для комп’ютерних систем. На початку кожного року вона розв’язує задачу заміни обладнання з метою забезпечення необхідного технологічного середовища розробки. Залежно від результатів експертної оцінки обладнення стан фірми (система S) характеризується як "добрий" (1), "задовільний" (2) і "поганий" (3), тобто система може знаходитися в одному із трьох указаних станів. Тоді матриця перехідних ймовірностей може мати вигляд:
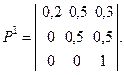
Якщо матриця перехідних ймовірностей не змінюється, то достатньо проаналізувати весь життєвий цикл системи S. Допустимо, що залежно від станів, в яких послідовно знаходиться система, може бути обчислено прибуток фирми. Логічно допустити, що прибуток за період 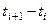 в значній мірі корелює з тим станом, в якому знаходилась фірма на початку періода, що розглядається, і в його кінці. Якщо, наприклад, у момент часу
в значній мірі корелює з тим станом, в якому знаходилась фірма на початку періода, що розглядається, і в його кінці. Якщо, наприклад, у момент часу 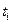 система знаходилась в "доброму" стані і в момент
система знаходилась в "доброму" стані і в момент 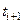 цей стан зберігся, то прибуток буде максимальним. Для моделювання цієї ситуації можна матриці перехідніх імовірностей
цей стан зберігся, то прибуток буде максимальним. Для моделювання цієї ситуації можна матриці перехідніх імовірностей 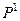 поставити у відповідність матрицю прибутків
поставити у відповідність матрицю прибутків 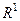 .
.
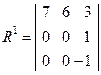
Елемент 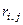 цієї матриці означає прибуток, отриманий за период
цієї матриці означає прибуток, отриманий за период 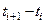 при переході системи із стану
при переході системи із стану 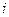 в стан
в стан 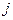 . Так, число 5 означає прибуток, виражений в деяких умовних одиницях, при збереженні системой "задовільного " стану. Від’ємні значення характеризують втрати.
. Так, число 5 означає прибуток, виражений в деяких умовних одиницях, при збереженні системой "задовільного " стану. Від’ємні значення характеризують втрати.
Маючи матриці 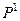 і
і 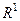 , можна достатньо просто прогнозувати результати функционування системи. Оскільки в часі обладнання потребує оновлення відповідно з новими міжнародними стандартами та вимогами ринку, то при незмінних матрицях
, можна достатньо просто прогнозувати результати функционування системи. Оскільки в часі обладнання потребує оновлення відповідно з новими міжнародними стандартами та вимогами ринку, то при незмінних матрицях 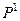 і
і 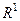 система може деградувати. У реально працюючих фірмах за результатами експертного анализу проводиться періодичне оновлення обладнення із зміною технологічного оточення та навчанням персоналу. Такий процес моделюється зміною матриць перехідних ймовірностей і прибутків. У нашому прикладі вони, наприклад, можуть помінятися таким чином:
система може деградувати. У реально працюючих фірмах за результатами експертного анализу проводиться періодичне оновлення обладнення із зміною технологічного оточення та навчанням персоналу. Такий процес моделюється зміною матриць перехідних ймовірностей і прибутків. У нашому прикладі вони, наприклад, можуть помінятися таким чином:
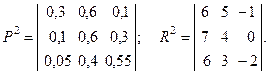
Тут в матриці прибутків враховано витрати на реорганізацію та модифікацію. Наприклад, елемент 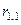 матриці
матриці 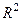 став менше відповідного елемента матриці R1. Таким чином, на кожному етапі виникає проблема вибору рішень з метою максимізації прибутку, що очікується.
став менше відповідного елемента матриці R1. Таким чином, на кожному етапі виникає проблема вибору рішень з метою максимізації прибутку, що очікується.
Для прикладу, що розглядається, розглянемо основні моменти вибору оптимального рішення. Допустимо, що планування 
 стратегії поведінки фірми здійснюється на кінцевий період часу. Покажемо, що рішення може бути отримано за вже відомим методом динамічного програмування (метод Беллмана) у відповідності із загальною концепцією аналіза й оптимізації багатокрокових задач. Нехай період
стратегії поведінки фірми здійснюється на кінцевий період часу. Покажемо, що рішення може бути отримано за вже відомим методом динамічного програмування (метод Беллмана) у відповідності із загальною концепцією аналіза й оптимізації багатокрокових задач. Нехай період 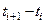 відповідає одному року, а планування здійснюється на трирічний період. Для наочності відповідне дерево рішень можна подати у вигляді графа, показаного на рис. 3.7.1. Тут кожний квадрат позначає розв’язуючу вершину і відповідає конкретному стану системи у визначений момент часу. Знак
відповідає одному року, а планування здійснюється на трирічний період. Для наочності відповідне дерево рішень можна подати у вигляді графа, показаного на рис. 3.7.1. Тут кожний квадрат позначає розв’язуючу вершину і відповідає конкретному стану системи у визначений момент часу. Знак 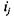 в середені квадрата означає, що в момент
в середені квадрата означає, що в момент  часу j, у'=1,2,3 (номер кроку) система знаходиться в стані 1', i = 1, 2, 3 (відповідно "добрий", "задовільний" або "поганий" стан). Дві стрілки, що виходять із кожної розв’язуючої вершины, відповідають двум альтернативам на кожному кроці:
часу j, у'=1,2,3 (номер кроку) система знаходиться в стані 1', i = 1, 2, 3 (відповідно "добрий", "задовільний" або "поганий" стан). Дві стрілки, що виходять із кожної розв’язуючої вершины, відповідають двум альтернативам на кожному кроці: 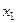 – проводити модернізацію (це верхня стрілка, яка визначає напрямок 1), або
– проводити модернізацію (це верхня стрілка, яка визначає напрямок 1), або 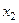 – не проводити (це нижня стрілка, яка визначає напрямок 2). Кружочки означають "випадкові" вершини, перехід із яких здійснюється у відповідності з вибраною матрицею перехідних імовірностей.
– не проводити (це нижня стрілка, яка визначає напрямок 2). Кружочки означають "випадкові" вершини, перехід із яких здійснюється у відповідності з вибраною матрицею перехідних імовірностей.
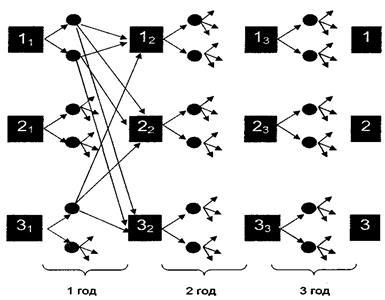
Рисунок 3.7.1– Дерево рішень
Згідно із загальним алгоритмом динамічного програмування, розв’язуємо задачу з кінця, рухаючись справа- наліво по розв’язуючим вершинам. Почнемо з вершини 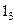 . Тоді при прийнятті рішення
. Тоді при прийнятті рішення 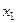 (без модернізаціїи) прибуток, що очікується, дорівнює
(без модернізаціїи) прибуток, що очікується, дорівнює
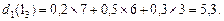
При виборі рішення 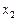 (модернізація) маємо:
(модернізація) маємо:
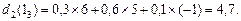
Число 5,3 більше числа 4,7, тому із вершини 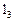 слід йти по напрямку 1, а сама вершина позначається числом 5,3. Стрілка 1 так само виділяється.
слід йти по напрямку 1, а сама вершина позначається числом 5,3. Стрілка 1 так само виділяється.
Далі переходимо до вершини 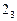 . Отримуємо значення двох прибутків залежно від рішень, що приймаються:
. Отримуємо значення двох прибутків залежно від рішень, що приймаються:
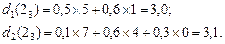
Вершина 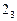 позначається числом 3,1 і виділяється напрямок 2. Для вершини
позначається числом 3,1 і виділяється напрямок 2. Для вершини 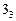 отримаємо:
отримаємо:
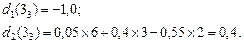
Вершина 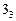 позначається більшим числом 0,4 і виділяється напрямок 2.
позначається більшим числом 0,4 і виділяється напрямок 2.
Одержані числа 5,3, 3,1, 0,4 характеризують один акт зміни стану і локальний прибуток, що при цьому отримується. Далі ці обчислення вже не повторюються, а значення цих локальних прибутків знадобляться в подальших розрахунках.
Перейдемо тепер до початку другого року. Почнемо з вершини 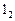 . При виборі напрямку (рішення) 1 маємо:
. При виборі напрямку (рішення) 1 маємо:
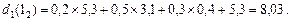
 Тут число 5,3 характеризує локальний прибуток этапа (розрахований раніше), а інші доданки характеризують найкращий прибуток, що очікується, отриманий на залишившихся етапах. Для другого варіанту рішення для цієї же вершини маємо:
Тут число 5,3 характеризує локальний прибуток этапа (розрахований раніше), а інші доданки характеризують найкращий прибуток, що очікується, отриманий на залишившихся етапах. Для другого варіанту рішення для цієї же вершини маємо:
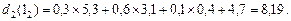
Число 8,19 більше числа 8,03, тому вершину 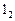 позначаємо числом 8,19 і виділяємо стрілку 2.
позначаємо числом 8,19 і виділяємо стрілку 2.
Для вершин 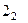 і
і 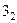 здійснимо аналогіичні розрахунки:
здійснимо аналогіичні розрахунки:
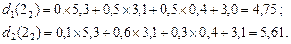
Вибираємо число 5, 61 і виділяємо стрілку 2. Далі маємо:
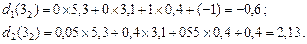
Для першого этапу аналогічно отримаємо:
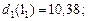
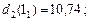
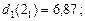
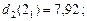
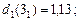
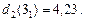
Тепер зворотна процедура динамічного програмуваннязавершена і, рухаясь від початку дерева рішень до кінця, можна "прочитати" оптимальне рішення: числа 10,74; 7,92; 4,23 означають оптимальний прибуток, що очікується, якщо відповідно система знаходилась на початку в станах 1, 2 і 3. Ці прибутки, що очікуються, досягаються, якщо ми завжди будемо вести себе "оптимально", тобто відповідно з поміченими на дереві рішень стрілками. А саме: в якому б стані не знаходилась система на початку першого року, доцільним є рішення, пов’язане з модернізацією обладнення. Те саме відноситься до початку другого року (всі виділені стрілки спрямовано "вниз"). І тільки, якщо на початку третього року ми опинимось у стані 1, нам недоцільно проводити модернізацію обладнання фірми.
Таким чином, задачу, що розглядається, розв’язано.
3.8 Запитання та завдання для самопідготовки
1. Яка центральна задача статистичної теорії прийняття рішень?
2. Який алгоритм прийняття рішень за статистичним критерієм?
3. Що називається критерієм максимуму правдоподібності?
4. Який алгоритм прийняття рішень за критерієм ідеального спостерігача?
5. Який алгоритм прийняття рішень за статистичним критерієм Неймана-Пірсона?
6. Вибрати за номограмою (рис. 3.2.1) порогове значення критерію Неймана-Пірсона та його обґрунтувати.
7. Поясніть суть максимінного критерію.
8. Поясніть суть мінікаксного критерію.
9. Поясніть суть критерію рівноможливих станів природи.
10. Знайдіть оптимальну за максимінним критерієм стратегію для матриці виграшів (табл. 3.8.1):
Таблиця 3.8.1 – Матриця виграшів
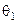
| 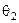
| 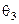
| |
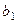
| |||
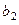
| |||
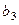
|
11. Знайдіть оптимальну за мінімаксним критерієм стратегію для матриці втрачених можливостей, побудованої із урахуванням матриці виграшів, заданої табл. 3.8.1.
12. Знайдіть оптимальну стратегію для матриці виграшів (табл. 3.8.1) за критерієм рівно можливих станів природи.
13. Який алгоритм визначення оптимальної стратегії за умов ризику?
14. Визначити оптимальну стратегію за матрицей виграшів (табл. 3.8.2).
Таблиця 3.8.2 – Матриця виграшів
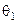
| 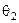
| |
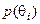
| 0,40 | 0,60 |
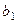
| ||
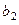
| ||
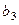
|
15. Побудувати графічно області вибору оптимальних стратегій залежно від імовірності 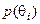 .
.
16. Яка стратегія називається байесівською?
17. Що називається змішаною стратегією? Поясніть суть використання змішаних стратегій.
18. Який процес називається марківським?
Дата добавления: 2016-02-20; просмотров: 1078;
