КОМБИНАЦИОННЫЕ СХЕМЫ

В комбинационных схемах логическая функция зависит только от комбинации значений входных переменных.

При описании многих цифровых устройств невозможно обойтись без упорядоченных двоичных наборов входных и выходных сигналов. Эти наборы удобно представлять в тех или иных системах счисления (СС).

НЕКОТОРЫЕ СИСТЕМЫ СЧИСЛЕНИЯ

В позиционных СС "вес" каждого разряда зависит от его позиции в числе. К числу непозиционных относится "римская" СС, например число - XVII.

Любое неотрицательное n-разрядное целое число C(n-1), C(n-2), ... ,C1,C0 в позиционной системе счисления может быть представлено в виде:

D = C_n-1*b^n-1 + C_n-2*b^n-2 + ... + C₁*b¹ + C₀*b⁰ (15)

где D - десятичный эквивалент числа, Ci - значение i-го разряда, b - основание системы счисления, b в степени i - вес (весовой коэффициент) i-го разряда и n число разрядов целой части числа. В цифровой и вычислительной технике наиболее распространены двоичная (BIN), десятичная (DEC), шестнадцатиричная (HEX) и непозиционная двоично-десятичная (BCD) системы счисления. В BCD системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая цифра i-го разряда кодируется 4-мя двоичными цифрами. Восьмиричная СС(OCT) применяется реже. В 16-ной системе счисления цифры от 0 до 9 совпадают с десятичными, а для ЦИФР болше 10 используются буквы латинского алфавита : A(a) = цифра 10, B(b) = 11, C(c) =12, D(d) = 13, E(e) =14. Двоичное число преобразуется в десятичное беззнаковое число по формуле (15), например 10010011 = 1*2⁷ + 1*2⁴ + 1*2¹ + 1*2⁰ = 147 (DEC). Для перевода числа из двоичной системы в 16 - ную, его необходимо разбить начиная справа на группы по 4 двоичных цифры и в каждой четверке просуммировать веса (8,4,2,1) соответствующие единичным значениям Ci. Для обратного перевода каждая HEX цифра заменяется четверкой двоичных, незначащие нули слева, если они есть, отбрасываются.

Двоично-десятичное число можно записывать и десятичными цифрами, например 1998, и двоичными - 0001 1001 1001 1000. Каждое десятичное число можно представить в виде BCD, например 19(DEC) = 19(BCD), но их двоичные представления не равны: 10011(19DEC) не равно 1 1001(19BCD). Не каждая запись из нулей и единиц имеет двоично-десятичный эквивалент. Например, 11001001(BIN) = [C9(HEX),201(DEC)] = ?(BCD), т.к. десятичной цифры 1100=12 не существует.

ДЕШИФРАТОР

Дешифратор (ДШ) преобразует двоичный код на входах в активный сигнал на том выходе, номер которого равен десятичному эквиваленту двоичного кода на входах. В полном дешифраторе количество выходов m = 2ⁿ, где n - число входов. В неполном ДШ m < 2ⁿ. По определению полный ДШ должен генерировать 2ⁿ выходных ЛФ, определенных на всех наборах из n - входных переменных, т.е. минтермов. Рассмотрим ДШ с n=2 и m=4, называемый также дешифратором "2 в 4" и дополним его входом разрешения выходов OE. Активным уровнем сигнала на прямых входах/выходах будет 1, а на инверсных - 0. По этому определению заполним таблицу истинности, где величина x может принимать любые значения.

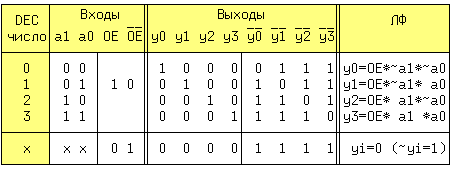
Таблица Карно для выхода y0 и 3-х входных переменных будет иметь вид:

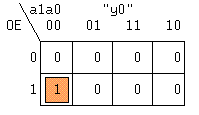
Прямоугольник, составленный из 1-ных клеток содержит только одну такую клетку, поэтому логическая функция выхода y0 будет иметь вид: y0 = OE*~a1*~a0. Аналогично получены остальные три уравнения. Преобразуем полученные для yi уравнения с помощью аксиомы двойного отрицания к базису И-НЕ: y0 = ~(~(OE*~a1*~a0)). Решению соответствует схема на рис.13.

Схема обведенная "..." имеет условное обозначение (A), а схема в запятых - обозначение (Б). Возможны также еще 2 комбинации прямых и инверсных входов и выходов В и Г.

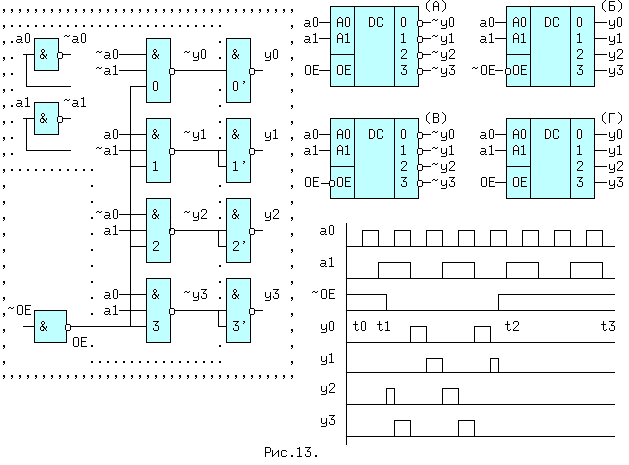
Пояснить работу ДШ можно с помощью временных диаграмм для схемы (Б). Во время действия сигнала ~OE=1 на нижних входах элементов И-НЕ(0..3) присутствует OE=0, и независимо от значений a0,a1, выходные значения ~yi=1, а yi=0, что и видно из рис.13. В эти отрезки времени t0..t1 и t2..t3 выходы "запрещены", т.е. на прямых выходах yi устанавливается пассивный уровень "0", а на инверсных выходах пассивная "1". В интервале t1..t2 сигнал ~OE=0(OE=1) и значения yi зависят только от переменных a1,a0. Если код на входах A1A0=10, что соответствует десятичной двойке, на входах второго элемента И-НЕ соберутся 3 логических "1". Сигнал ~y2=0, а y2=1, что видно на диаграмме y2. Вместо инвертора OE,может применяться более сложная схема,показанная на рис.14. Здесь OE=1 в случае,когда ~OE1 = ~OE2 = 0 и OE3 = 1.

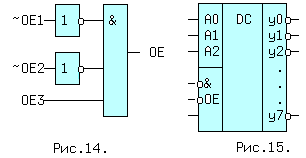
Такая схема применяется в дешифраторе "3 в 8" типа 1533ИД7(555ИД7), условное обозначение которого приведено на рис.15. Дешифраторы широко применяются в вычислительной технике, как часть больших интегральных схем, для выбора одного из нескольких внешних устройств (ВУ) при обмене данными между ним и микропроцессором. В этом случае на входы ai подаются сигналы, называемые адресом ВУ, а входы называются адресными.

ДЕМУЛЬТИПЛЕКСОР

Устройство передающее сигнал с информационного входа на один из выходов, причем номер этого выхода равен десятичному эквиваленту двоичного кода на адресных входах, называется демультиплексором (ДМ). В качестве ДМ может использоваться дешифратор, у которого вместо сигнала OE подается информационный сигнал x. Например, если на входы подать код a1a0=10(BIN)=2(DEC), то сигнал x появится на выходе y2, а на остальных выходах yi=0. На рис.16. даны условное обозначение ДМ "1 в 4" и его механический аналог.