Изотермы адсорбции.

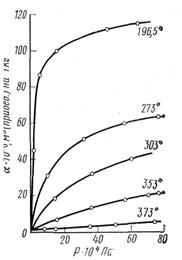Как показали исследования, адсорбция увеличивается с ростом давления (концентрации) газа, однако это увеличение не беспре­дельно. Для каждого адсорбируемого га­за (при t = const) через некоторое время над адсорбентом устанавливается пре­дельная величина адсорбции, отвечающая равновесию между обеими фазами. Кри­вая зависимости адсорбции от давления (концентрации) при постоянной темпера­туре носит название изотермы адсорбции. Она является одной из важнейших харак­теристик адсорбционных процессов. На рис. 5.2 изображены типичные изотермы адсорбции СО₂ углем при различных тем­пературах, взятые из работы А. А. Ти­това.

Как видно из рис. 5.2, повышение дав­ления газа Рис 5.2 увеличивает адсорбируемое количество его. Однако на разных участ­ках изотермы адсорбции это влияние ска­зывается неодинаково .

Наиболее силь­ным оно оказывается в области низких давлений, где адсорбция подчиняется закону Генри для раствори­мости газов в жидкостях, т. е. она прямо пропорциональна давлению газа.

Дальнейшее повышение давления тоже увеличивает количество адсорбированного газа, но уже во все уменьшающейся степени. И, наконец, при достаточно высоких давлениях кривая стремится к прямой, параллельной оси абсцисс. В этом случае достигнуто полное насыщение адсорбента и повышение давления газа уже не влияет на его адсорбцию.

Таким образом, между адсорбцией и давлением (концентрацией) газа отсутствует прямая пропорциональная зависимость. Это и вызвало необходимость найти математическое выражение, которое достаточно точно описало бы экспериментальные данные. Впервые эмпирическое уравнение, которым пользуются и в настоящее время, было предложено Фрейндлихом. Это уравнение имеет следующий вид:

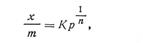
5.3

где х/m— величина адсорбции на единицу массы адсорбента; р — равновесное давление газа над поглотителем (для растворов поль­зуются равновесной концентрацией С), К и 1/n — константы ад­сорбции, характерные для данного процесса адсорбции в опреде­ленных пределах, значение которых можно найти из опытных дан­ных.

Рассмотрим, как определяются численные значения констант. На рис. 5.3, а дано графическое изображение уравнения для слу­чая адсорбции из жидкости. По оси абсцисс отложены равновес­ные концентрации С (кмоль/м³), по оси ординат — значения х/m

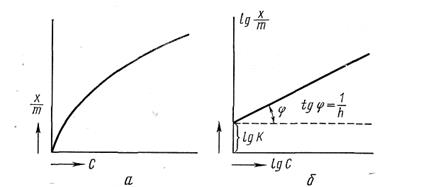
Рис 5.3

(кмоль/кг). Если прологарифмировать уравнение (5.3), получим следующее выражение:

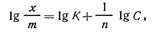
5.4

из которого можно найти значения постоянных К 1/п. Для этой цели построим график, выражающий зависимость lg х/m — lg С. Получается прямая линия (рис. 5.3 ,б), отсекающая на оси орди­нат отрезок, равный lg К, а тангенс угла наклона этой прямой к абсциссе дает значение 1/n.

Уравнение (5.4) есть уравнение прямой линии. Несмотря на то, что уравнение Фрейндлиха широко применяется на практике, оно имеет определенные недостатки. Многочисленные исследования показали, что значение адсорбции, вычисляемое на основании этого уравнения, не соответствует данным опыта в области малых и боль­ших концентраций. Константы К и 1/n являются чисто эмпириче­скими и не имеют реального физического смысла.

Позднее (1917) Ленгмюр вывел простейшее уравнение адсорб­ции для случая адсорбции газа на гладкой твердой поверхности (стекло, слюда, монокристаллы), оказавшееся в дальнейшем при­менимым и к другим поверхностям раздела. При выводе своего уравнения Ленгмюр исходил из допущения, что адсорбционный слой мономолекулярен, т. е. только один слой молекул связан си­лами молекулярного сцепления с поверхностью. При этом указан­ный слой полностью поглощает собой все адсорбционные силы по­верхности адсорбента, поэтому образование второго слоя адсорби­рованных молекул исключается.

Число активных мест поверхности ученый принял равным еди­нице, а долю активных мест, связанных с адсорбированными моле­кулами, обозначил через х. При этом условии свободная часть по­верхности равняется 1—х. Обозначив величину адсорбции через Г и учитывая, что при х=0, Г = 0 и при х=1, Г = Г_∞, он нашел, что х=Г/Г_∞, где Г — количество вещества, адсорбированное единицей поверхности при полном насыщении.

Тогда уравнение Ленгмюра можно записать:

Г = Г∞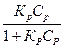

5.5

Опыт показывает, что уравнение изотермы адсорбции Ленгмю­ра сравнительно удовлетворительно дает количественную характе­ристику адсорбции при низких и при высоких концентрациях по­глощаемого вещества. В отличие от уравнения изотермы Фрейндлиха все величины, входящие в уравнение Ленгмюра, имеют опреде­ленный физический смысл и вполне обоснованы теоретически. Уравнение Ленгмюра исходит из расчета мономолекулярного адсорбционного слоя.

Однако не все ученые разделяют эту точку зрения. По мнению Поляни и ряда других авторов, возможен мно­гослойный адсорбционный слой, причем эта точка зрения имеет некоторое теоретическое и опытное обоснование.

По теории Ленгмюра молекулы адсорбтива, притянутые к от­дельным активным точкам, между собой не взаимодействуют. Од­нако при накоплении в адсорбционном слое молекул веществ, об­ладающих высокой молекулярной массой, между ними могут воз­никнуть значительные силы сцепления. В этом случае уравнение Ленгмюра дает неверные результаты. В ряде случаев, в частности при применении пористых адсорбентов, таких, как уголь, силикагель и др., формула Фрейндлиха дает лучшие результаты, чем уравнение Ленгмюра.

Изотерма Брунауэра – Эммета – Теллера (БЭТ) см. рис.5.4.

Теория адсорбции БЭТ исходит из:

1) адсорбционный слой имеет непостоянную толщину на поверхности адсорбента;

2) тепловой эффект адсорбции ≠ тепловому эффекту конденсации адсорбтива;

3) центры адсорбции – двумерные ячейки на поверхности адсорбента;

4) латеральное взаимодействие отсутствует.

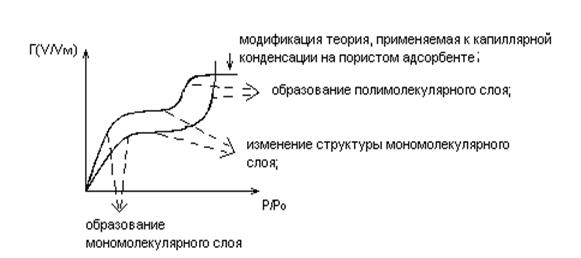
Рис. 5.4

При малых P/P₀ изотерма БЭТ переходит в изотерму Ленгмюра.

Достоинство:

1)учитывает полимолекулярность слоя адсорбтива.

Недостатки:

1) не учитывает латеральные взаимодействия.

На основе БЭТ – изотермы рассчитывают величину адсорбции для конкретных систем.