Параметрические колебания.
Колебания механических систем, которые приходят в движение не под действием вынуждающих сил, а вследствие периодического изменения параметров самой системы (инерционность, жесткость, геометрические размеры), называются параметрическими (рис.4.1). Примеры на первых двух рисунках соответствуют периодическому изменению инерционных нагрузок за счет изменения геометрических параметров системы; они относятся к случаю периодического изменения обобщенного коэффициента инерции.
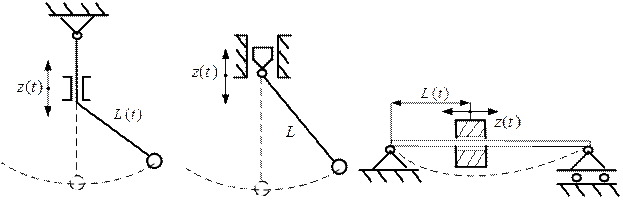
Рис.4.1
Причины возникновения параметрических колебаний несложно понять, рассмотрев один практический пример - раскачивание качелей приседанием человека в верхнем положении и вставанием в нижнем.
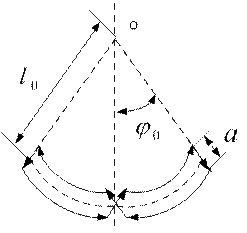
Рис.4.2
Для простоты заменим качели математическим маятником массы 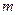 , «длина»
, «длина» 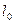 которого изменяется скачкообразно на величину
которого изменяется скачкообразно на величину 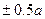 , где
, где 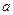 - понижение центра тяжести человека при приседании (рис.4.2). Надо сделать замечание, касающееся длины маятника. Под длиной маятника следует понимать не длину нити, а расстояние от точки подвеса до центра тяжести подвешенного груза. Нетрудно выполнить расчет величины энергии
- понижение центра тяжести человека при приседании (рис.4.2). Надо сделать замечание, касающееся длины маятника. Под длиной маятника следует понимать не длину нити, а расстояние от точки подвеса до центра тяжести подвешенного груза. Нетрудно выполнить расчет величины энергии 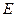 , поступающей для раскачивания маятника за половину одного периода. При приседании в отклоненном положении высвобождается энергия, равная работе силы тяжести
, поступающей для раскачивания маятника за половину одного периода. При приседании в отклоненном положении высвобождается энергия, равная работе силы тяжести 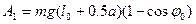 , где
, где 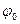 - угол наибольшего отклонения, а в нижней точке при подъеме центра тяжести необходимо затратить энергию
- угол наибольшего отклонения, а в нижней точке при подъеме центра тяжести необходимо затратить энергию 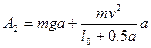 , где
, где 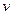 - скорость в нижней точке траектории. Тогда, с учетом
- скорость в нижней точке траектории. Тогда, с учетом 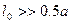 и малости угла
и малости угла 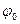 ,
, 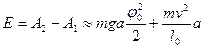 . Если величина поступающей энергии окажется больше потерь энергии на преодоление сопротивления, которое всегда имеет место в реальных конструкциях, то будет происходить раскачивание маятника (качелей). Более подробно процесс колебаний качелей рассмотрен в [1, 8].
. Если величина поступающей энергии окажется больше потерь энергии на преодоление сопротивления, которое всегда имеет место в реальных конструкциях, то будет происходить раскачивание маятника (качелей). Более подробно процесс колебаний качелей рассмотрен в [1, 8].
Основная цель исследования параметрических колебаний состоит в определении диапазона изменения параметров, являющихся причинами возникновения колебательного процесса с точки зрения его устойчивости. То есть если периодически изменяющиеся параметры самой системы (масса, жесткость, геометрические размеры) приводят к колебательному процессу с нарастающей амплитудой колебаний (параметрический резонанс), то движение считается неустойчивым, а область, в которой происходит изменение этих параметров, называется областью неустойчивости. Диапазон, в котором лежат периодически изменяющиеся параметры механической системы, приводящие к затухающим колебаниям, называется областью устойчивого движения. С точки зрения энергетического состояния механической системы важно знать, увеличивается ли ее полная механическая энергия за период колебаний или уменьшается. При устойчивом движении происходит уменьшение энергии, а при неустойчивом движении – увеличение. Для определения диапазонов изменения периодически изменяющихся параметров, соответствующих областям устойчивости и неустойчивости, необходимо составить уравнение колебательного движения механической системы и получить его решение хотя бы в приближенной форме. Дальнейшее исследование этого решения позволит установить диапазоны изменения параметров системы, соответствующие областям устойчивого и неустойчивого режимов движения.
Без особых затруднений можно прейти к математическому описанию параметрических колебаний, рассмотрев в качестве примера параметрические колебания маятника, точка подвеса которого перемещается по вертикали с течением времени (рис.4.3).
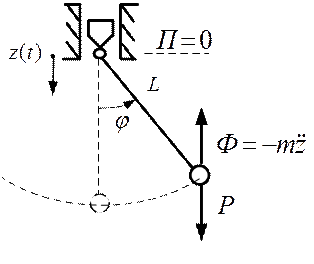
Рис.4.3
Это механическая система с одной степенью свободы, так как закон вертикального перемещения опоры 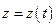 задан. Для описания относительного колебательного движения механической системы будем использовать угловую обобщенную координату
задан. Для описания относительного колебательного движения механической системы будем использовать угловую обобщенную координату 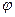 . Уравнение относительного движения можно записать в виде
. Уравнение относительного движения можно записать в виде
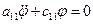 ,
,
где 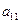 и
и 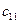 - обобщенные коэффициенты инерции и жесткости соответственно. Их значения подсчитываются следующим образом с помощью вычисления кинетической и потенциальной энергий:
- обобщенные коэффициенты инерции и жесткости соответственно. Их значения подсчитываются следующим образом с помощью вычисления кинетической и потенциальной энергий:
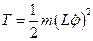 ;
; 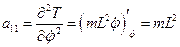 .
.
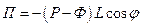 ;
; 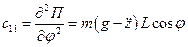 .
.
Для малых углов отклонения 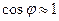 , коэффициент жесткости равен
, коэффициент жесткости равен
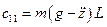
Уравнение колебательного движения принимает вид
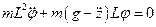 ,
, 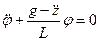 (4.1)
(4.1)
Это дифференциальное уравнение с переменными коэффициентами. Обобщая рассмотренный пример, уравнение параметрических колебаний для механических систем с одной степенью свободы можно записать в виде
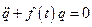 .
.
При решении этого уравнения возникают серьезные математические трудности. В литературе приводятся решения для некоторых частных случаев.
Уравнение Мейснера 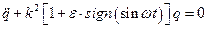 ;
;
график изменения функции 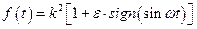 изображен на рис.4.4;
изображен на рис.4.4;
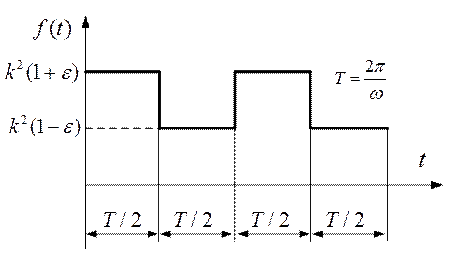
Рис.4.4
Уравнение Матье 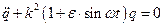 ;
;
Уравнение Хилла 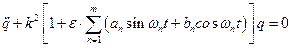 .
.
Дата добавления: 2016-02-11; просмотров: 4948;
