Дәріс. Комбинациялық құрылғылардың анализі мен синтезі

Дәріс мазмұны:комбинациялық құрылғылардың синтезінің кезеңдері, типтік комбинациялық сұлбалардың жұмысының анализі.

Дәріс мақсаты:логикалық функциялардың көрініс түрлерін зерттеу, оларды минимизациялау әдістерін және құрылымдық сұлбалардың құрылуын үйрену, типтік комбинациялық микросұлбалар жұмысының анализінің дағдысын алу.

Комбинациялық құрылғы (КҚ) –бұл шығысы кірісінің күйіне байланысты анықталатын логикалық құрылғы, яғни дәл сол уақытта кірістік айнымалылардың қайсысы беріліп жатқанына байланысты. 3-суретте үш кірісі және бір шығысы бар КҚ көрсетілген.

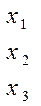
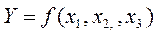
3-сурет – үш кірісті комбинациялық құрылғыға мысал

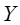логикалық функциясын үш кірістік айнымалылар үшін арналған шынайылық кестесімен берсе болады.

2-кесте

N

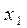
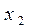
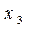
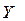
2-кестенің бағаналарында кірістік айнымалылар мәндері мен оларға сәйкес келетін берілген логикалық функциялардың мәндерінің ықтималды жиынтықтары.

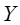логикалық функциясын құрылымдық формуламен берсе болады, яғни теңдікпен, оның сол жағында логикалық функцияны білдіретін әріп жазылған, ал оң жағында – логикалық өрнек. Логикалық қосу, көбейту және терістеу белгілерімен қосылған екілік айнымалылары бар жазу логикалық өрнек деп аталады.

Құрылымдық формуланы жазудың екі түрі бар: жетілген дизюнктивті нормалы форма (ЖДНФ) және жетілген конъюктивті нормалы форма (ЖКНФ).

ЖДНФ – минтермдер логикалық қосындысы, олардың логикалық функциясы 1-ге тең. Минтерм – бұл терістеумен немесе терістеусіз көрсетілген кіріс айнымалыларының логикалық туындысы. 2-кестеге сәйкес ЖДНФ түріндегі құрылымдық формуланы жазып қояйық, терістеу белгілерін 0-ге тең кірістік айнымалылардың үстіне қоямыз:

.

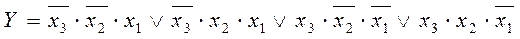Әр кірістік айнымалылардың жиынтығына, өзінің ондық эквиваленті сәкес келетіндіктен, құрылымдық формуланы қысқа түрде көрсетсе болады

.

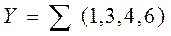ЖКНФ – бұл макстермдер логикалық қосындысы, олардың логикалық функциясы 0-ге тең. Макстерм – бұл терістеумен немесе терістеусіз көрсетілген кіріс айнымалыларының логикалық қосындысы. 2-кестеге сәйкес, терістеу белгісі 1-ге тең кірістік айнымалылардың үстіне қойылатынын ескере отырып, ЖДНФ құрылымдық формуласын жазып қояйық:

.

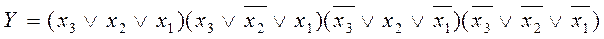Құрылымдық формула қысқа түрінде былай жазылады

.

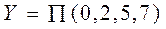Құрылымдық формулаларды минимизациялау үшін келесі әдістер қолданылады: а) Карно карталарының графикалық әдісі немесе Х ≤ 5 аргументтер саны кезіндегі Вейч диаграммалар әдісі; ә) Х > 5 кезінде Мак-Класки әдісі [ 6 ].

Жоғарыда келтірілген құрылымдық формулаларды минимизациялауға Карно карталар әдісімен мысал келтірейік. Карта торларының санын 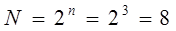формуласымен анықтайды, мұндағы n – кіріс саны.

4-суретте 2-кесте бойынша толтырылған Карно картасы келтірілген. 4-суреттен көрініп тұрғандай, Х₃Х₂Х₁ кірістік айнымалыларының әр жиынтығына сәйкес келетін торға логикалық функцияның өзінің мәні сәйкес келеді.

ЖДНФ:1 логикалықтарын біріктіреді

ЖКНФ:0 логикалықтарын біріктіреді

			1

00 01 11 10

0

4-сурет – сегіз торлы Карно картасы

Картадағы торларды сандағы екі модуль бойынша біріктіруге болады (2,4,8,16), горизонталь немесе вертикаль бойынша, бірге тұрған немесе қарама-қарсы жақта тұрғандары бойынша. Екі торды біріктірген кезде бір айнымалы жоғалады, төрт торды біріктіргенде – екі айнымалы, сегіз торды біріктіргенде – үш айнымалы, егер біріктірілген аймақта сол айнымалылар 1 және 0 қарама-қарсы мәндерін қабылдаса.

Осы ережелерді мысалымызға келтіре отырып, келесі минимизацияланған құрылымдық формулаларды аламыз:

ДНФ : 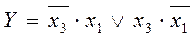; КНФ: .

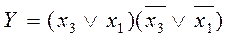Шыққан өрнектерге анализ жасай отырып, мынадай қорытындыға келеміз: олардың негізгі базистегі (ЖӘНЕ,НЕМЕСЕ,ЕМЕС) сұлбалық жүзеге асырылуы үшін бірдей бірнеше логикалық элемент (бес дана) қажет. ЖӘНЕ-ЕМЕС немесе НЕМЕСЕ-ЕМЕС универсалды базистерінде жүзеге асыру үшін өрнектердің үстіне екі терістеу қойып, де Морган ережесін қолдану керек:

,

.

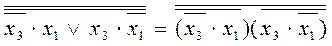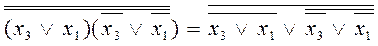Алынған өрнектерден көрініп тұрғандай, логикалық операциялар саны, сәйкесінше логикалық элементтер саны екі жағдайда да алтыға дейін өсті, бірақ логикалық элементтерді қолданудың біртиптілігі осы сұлбалы жүзеге асыруды жағымды етеді. 5-суретте ЖӘНЕ-ЕМЕС базисіндегі құрылымдыұ сұлбаның мысалы келтірілген.

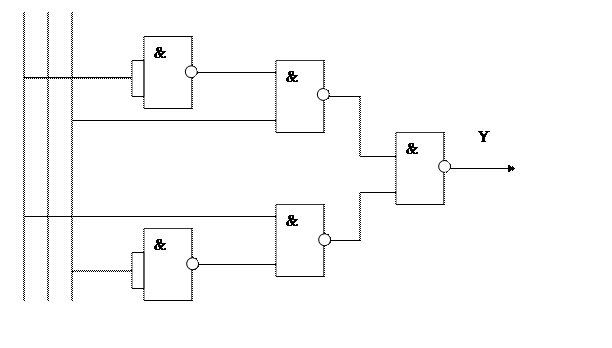
5-сурет – ЖӘНЕ-ЕМЕС базисіндегі комбинациялық құрылғының сұлбасы

Келтірілген мысалға қатысты мынадай қорытынды жасауға болады, КҚ синтезін бірқатар кезеңдерге бөлгеніміз абзал:

1) 1 логикалық функция сияқты ауызша берілетін, яғни ақиқат кестесі мен дайын құрылымдық функция, КҚ жұмыс істеу шарттарын жазу;

2) құрылымдық формуланы минимизациялау мен жазу;

3) құрылымдық сұлбаны құрастыру;

4) минимизацияланған құрылымдық формуланы берілген базис бойынша жазу.

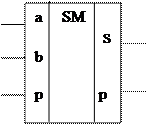
Сандық техникада күрделі құрылғыларды құрастырған кезде тек бөлек логикалық элементтерді ғана емес, олардың типтік құрылысы түріндегі комбинацияларын кеңінен қолданылады. Олар интегралды микросұлба түрінде біртұтас жұмыс істейді. 6-суретте 3 те 8 ұйымдастырылуы мен тік шығыстары бар дешифратор, ¼ ұйымдастырылуы бар демультиплексор, D ақпараттық кіріс, терістеуші шығыстар және 1,2 адрестік кірістер және толық сумматор тәріздес типтік комбинациялық құрылғылардың шартты белгіленулері көрсетілген.

Дешифратор (DC-decoder) кодтық комбинацияларды тану үшін арналған, олардың әр қайсысына сәйкес өзінің шығысы бар. Сол шығыста тура шығыс болған кезде логикалық 1 пайда болады, ал егер терістелген болса, логикалық 0. 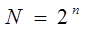теңдігінен дешифратордың шығыстар саны анықталады, мұндағы n – кіріс саны. Шифратор (CD-coder) дешифраторға қарама-қарсы операцияны орындайды, яғни кірісіне келетін ақпаратты кодтайды. Демультиплексор (DMS) бір ақпараттық кірістен таңдалған реттегі бір шығысқа ақпаратты өткізу үшін қолданылады. Қажет болған шығысты таңдау адрестік кірістерге келетін екілік код арқылы жүзеге асырылады.

Шығыс саны 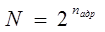өрнегінен анықталады, мұндағы 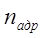- адрестік кірістер саны. Мультиплексор (MS) демультиплексорға қарама-қарсы мәселені шешеді, яғни ақпаратты қажет болған ретте бірнеше кірістен бір шығысқа жібереді. Осыған орай оның адрестік кірістеріне сәйкесінше екілік код беріледі. Сумматор(SM) – екілік немесе екілік-ондық сандардың арифметикалық қосындысын есептейтін құрылғы. Ең қарапайым сумматор 2 модулі бойынша сумматоры болып табылады. Ол ЕРЕКШЕЛЕЙТІН НЕМЕСЕ деп аталады. Оның екі кірісі мен бір шығысы бар және кірістеріне тең емес мәнді сигналдар (1 және 0) келген кезде ғана логикалық 1-ді көрсетеді. Сандық сұлбаларды жұптық пен тақтыққа тексеру үшін қолданылады. Толық сумматор бірразрядты екілік сандардың арифметикалық қосындысын есептеуге арналған, сол үшін оның 2 кірісі бар, ал үшіншісі ауысу кірісі болып табылады және көпразрядты сандарды қосу үшін керек. Сумматордың екі шығысы қосынды мен ауысудың пайда болуына қатысады.

6-сурет – Типтік комбинациялық құрылғылардың шартты белгіленулердің мысалдыры