Дәріс. Қалыптаспаған режимде ұңғыны зерттеу әдісі
Дәріс мақсаты:Ұңғыны тоқтатқаннан кейін түп қысымының қалпына келтіру жылдамдығын және ұңғыны іске қосқаннан кейін түп қысымының төмендеу жылдамдығын бақылау.
Дәріс жоспары: Қалыптаспаған режимде ұңғыны зерттеу. Қысымды қалпына келтіру әдісімен скважинаны зерттеу кезінде мәліметтері төмендегі тәртіппен өндеу. 1) 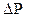 -
- 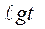 байланыс графигі құру; 2) График бойынша і және А анықтау.
байланыс графигі құру; 2) График бойынша і және А анықтау.
Қалыптаспаған режимде ұңғыларды гидравликалық әдіспен зерттеген кезде серпімді режим заңына сүйенеді. Қабаттың серпімді қасиеттері және сұйыққа қаныққан және тәуелсіз газ өлшемі қабат жүйесінен байқалады. Мұндай өзгерістер ауытқулар деп аталады, ал жұмыс режимі кезінде жылдам өзгеретін ұңғыларды, ауытқу ұңғыларында немесе ағынды ауытқуда.
Бір ұңғыдағы ауытқуды қарастырайық, ол үлкен тығыз қабатта үздіксіз жұмыс жасайды.
Ұңғы айналасындағы воронка депрессиясын қоректендіру нұсқасы деп аталады, ал воронка радиусы 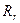 -қоректендіру нұсқасының радиусы. Нұсқаға қысым
-қоректендіру нұсқасының радиусы. Нұсқаға қысым 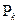 - әсер етеді, ал ұңғы түбіне орнатылған жұмыс кезінде – қысым Рс.
- әсер етеді, ал ұңғы түбіне орнатылған жұмыс кезінде – қысым Рс.
Егер ұңғыны бірден тоқтатсақ және жұмыс жасау режимін өзгертсек онда оның айналасында қысымды қайта бөлу процесі басталады. Нақты түсіндіріп айтатын болсақ ол кезде жүретін құбылыс ұңғы айналасындағы сұйық тығыздығының өзгеруін ескеру қажет. Қысым тығыздығының функциясы болып табылады 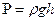
Мұнай тығыздығының нұсқасы үлкен мәнге ие болады. Ұңғыдағы өндіріліп жатқан мұнайды тоқтату кезінде контурдан мұнайдың саны түсе береді, ұңғыны тоқтатудың алдында ұңғы дебитінде тексертіледі.
Ұңғыны түсіру кезінде көп сондай құбылыстар пайда болады, тоқтату кезіндегідей, қысым түседі, воронка депрессиясы 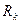 биіктігіне жеткенше өседі, айдау ұңғының жібергіштігі пайдаланумен сай келеді, ал айдау ұңғысының тоқтатылуы пайдалану жіберуіне сай.
биіктігіне жеткенше өседі, айдау ұңғының жібергіштігі пайдаланумен сай келеді, ал айдау ұңғысының тоқтатылуы пайдалану жіберуіне сай.
Қисықтарды қалпына келтіруді барлық ұңғыларда кездестіруге болады, ол пайдалану мен белгілеуіне тәуелді емес. Қисықтарды қалпына келтіруді алу ұңғыны тоқтатқаннан кейін пайда болады. Оны режимнің жұмыс кезінде дебит төмендеген кезде алуға болады, керісінше дебит жоғарылаған кезде қисық қысымның құлауын аламыз. Осылайша қисық қысымды қалпына  келтіру үшін ұңғыны тоқтату міндетті емес. Ол үшін келесі формуланы қолданады, ұңғыдағы сұйық тығыздығының ағынын гидродинамикалық жер асты есептеулеріне пайда болған онда қисықты қалпына келтіру қысымы алынады.
келтіру үшін ұңғыны тоқтату міндетті емес. Ол үшін келесі формуланы қолданады, ұңғыдағы сұйық тығыздығының ағынын гидродинамикалық жер асты есептеулеріне пайда болған онда қисықты қалпына келтіру қысымы алынады.
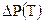 =
= 
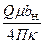
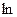
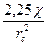 +
+ 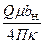
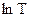 (13)
(13)
мұндағы Q-ұңғы дебиті, 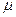 -тұтқырлық,
-тұтқырлық, 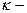 өтімділік, h-қабат қалыңдығы,
өтімділік, h-қабат қалыңдығы, 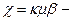 өткізгіштік, мұндағы
өткізгіштік, мұндағы 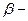 орташа коэффициент тығыздығының көлемі, t-ұңғыны тоқтатқанда немесе жіберген кездегі уақыт:
орташа коэффициент тығыздығының көлемі, t-ұңғыны тоқтатқанда немесе жіберген кездегі уақыт:
У= 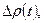 а=
а= 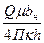 ln
ln 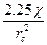
 (14)
(14)
x=ln t, b= 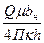 (15)
(15)
1-ші теңдікті қайтадан былай жазамыз яғни 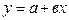 бұл түзу теңдігі болып табылады.
бұл түзу теңдігі болып табылады.
Сондықтан, ұңғы түбіндегі қисық қысымды қалпына келтіреді 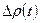 ,
, 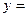
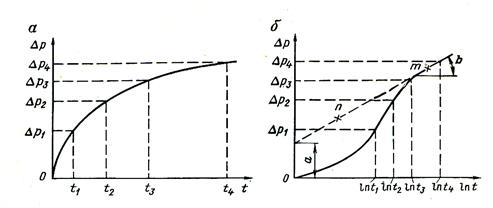
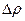 жартылай графикалық координат: x=ln t, у және
жартылай графикалық координат: x=ln t, у және 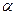 осіндегі ісінетін түзу түрінде болады; мағынасын 2-ші формула бойынша анықтаймыз, b бұрыштық коффициент, 3-ші формула бойынша анықталады.
осіндегі ісінетін түзу түрінде болады; мағынасын 2-ші формула бойынша анықтаймыз, b бұрыштық коффициент, 3-ші формула бойынша анықталады.
ҚҚҚ ұңғы түбіне ұңғыны белгілейтін монометр орналастырады. Мұндай монометр ұңғы түбіне түсіріледі ол өзгеру 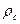 көрсеткіші t уақыт функциясында байқалады. Сондықтан шынында
көрсеткіші t уақыт функциясында байқалады. Сондықтан шынында 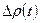 қисығын
қисығын 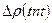 -ны кординатасына қайтадан өзгертеміз де а және в күнделікті коэффициент табамыз. Бастапқы ҚҚҚ аймағы түзуге тиісті болмайды ол соңғы ағынға байланысты болады және сұйық маскасының инерциясы ол 1-ші формулада мүлде қарастырылмайды.
-ны кординатасына қайтадан өзгертеміз де а және в күнделікті коэффициент табамыз. Бастапқы ҚҚҚ аймағы түзуге тиісті болмайды ол соңғы ағынға байланысты болады және сұйық маскасының инерциясы ол 1-ші формулада мүлде қарастырылмайды.
Қайтадан салынған 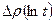 қисығында түзу сызқықты аймақ қарастырылады ол екі нүктелі коэффициент арқылы анықталады:
қисығында түзу сызқықты аймақ қарастырылады ол екі нүктелі коэффициент арқылы анықталады:
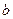 =
= 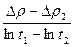 (16)
(16)
b-анықтап, 3-ші формуладан сұйық өткізгіштікті Е= 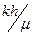 -ды анықтауға болады:
-ды анықтауға болады:
Е= 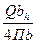 (17)
(17)
Енді белгілі болған Е-нан 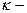 өткізгіштік анықталады:
өткізгіштік анықталады:
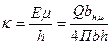 (18)
(18)
1-ші формуладан ұңғыдағы анықталмаған радиусын анықталған:
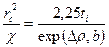 (19)
(19)
Арықталмаған режимде ұқсас әдіспен айдау ұңғыларын зерттеген. КВД-дан айдау ұңғыларын алу үшін дебитпен Q ұзақ уақыт жұмыс жасаған ол үшін саға басында ысырманы жауып айдауды және қисық құлауды 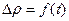 тоқтату керек.Ұзындық
тоқтату керек.Ұзындық 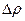 қысыммен сағадағы орнатылған айдау режимін және т.б айдау қысымы,сағадағы ағынды қысым.
қысыммен сағадағы орнатылған айдау режимін және т.б айдау қысымы,сағадағы ағынды қысым.
Аналитикалық ақпарат айдау ұңғыларымен анықталмаған режим үшін арналған,ол 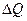 ұзындық дебитіндегі сатылы өзгерісін өңдеу үшін тиімді.Дебиттің сатылы өзгерісі штуцермен ысырманы өзгерткен кезде жүзеге асуы мүмкін. Бұл жағдайда ұңғы манометірінде ҚҚҚ
ұзындық дебитіндегі сатылы өзгерісін өңдеу үшін тиімді.Дебиттің сатылы өзгерісі штуцермен ысырманы өзгерткен кезде жүзеге асуы мүмкін. Бұл жағдайда ұңғы манометірінде ҚҚҚ 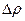 (t) байқалады сонда бастапқы дебит Q
(t) байқалады сонда бастапқы дебит Q 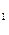 жаңа дебитке Q
жаңа дебитке Q 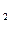 ұзындық өзгерісі Q=Q
ұзындық өзгерісі Q=Q 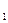 -Q
-Q 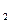 тәуелді.Берілген формуладағы Q–ға
тәуелді.Берілген формуладағы Q–ға 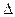 Q-ды қою керек.Нәтижесі өзгеріссіз қалады.
Q-ды қою керек.Нәтижесі өзгеріссіз қалады.
Анықталмаған режимдегі қабат айналасындағы өткізбейтін немесе өткізетін қасиетінің қаншалықты тиімді екені анықталады. Бұрышты коэффицент b аяғында өткізгіштік төменде, онда b өткізгіштігі жоғарылайды.
5.1 Теориялық негіздері.
Зерттеудің негізінде пьезоөткізгіштік теңдеуі жатыр:
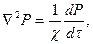 (34)
(34)
мұндағы 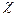 — пьезоөткізгіштік коэффициенті, м2/с;
— пьезоөткізгіштік коэффициенті, м2/с;
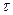 - уақыт, с.
- уақыт, с.
Біркелкі ерітіндімен толтырылған шексіз қабатта орналасқан бір ұңғы үшін уақыт және аймақтың шеңберінде айналасындағы қысымның өзгерісі былай жасалуы мүмкін:
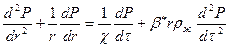 (35)
(35)
мұндағы ρж – қабат сұйықтығының тығыздығы, кг/м3;
β* — серпімді сыйымдылық коэффициенті, м2/Н, (1) теңдеуімен анықталады.
Оң жақ бөліктегі екінші бөлінді инерциялық мүшені көрсетеді. Инерциялық мүшені бөлу арқылы (35) Фурье теңдігі алынады:
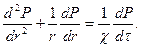 (36)
(36)
9-суретте ұңғының тоқтаган уақытындағы дебиті мен қысымының графикалық өзгерісі көрсетілген.; Р(Т) — үздіксіз Q дебиті Т уақыттығы жұмыс істеу кезіндегі қысымның өзгеруі. T уақыттан бастап, уақытқа (ұңғының тоқтаған уақыты) дейінгі ұңғы түбінің Pзаб(t) қысымы орнына келтірілгені көрсетіледі. (9 суретті қараңыз) келесі теңдіктерді жазамыз.
ΔP1(t)=-P(T)+Pзаб(t), (37)
ΔP2(t)=Pпл+Pзаб(t), (38)
мұндағы Р(Т) — қысымы, егер ұңғы зерттеу үшін тоқтатылмаған болса, t уақытқа (тоқтатылған уақыты), дейін деп қысыммен жұмыс істеген болар еді. (9 суретте штрихтік сызықпен көрсетілген );
Рпл — қабат қысымы;
Pзаб(t) — ұңғы зерттеуге тоқтатылған уақыттағы оның түбінің қысымы.
Қорытындысында (36) теңдікті былай шешеміз:
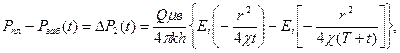 (39)
(39)
мұндағы Q — ұңғы Т уақыттан тоқтатылғанға дейін жасалған үздіксіз дебит;
в — қабаттағы сұйықтықтың колемді коэффиценті (мұнйдың);
eI — экспоненциалды интегралды функцияның белгісі.
T>>t болғандықтан (39) теңдік былай болады:
- 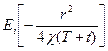 ≈
≈ 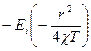 (40)
(40)
τ = Т уақыт ішіндегі қысымның түсуі былай шығарылады:
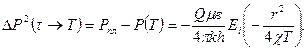 (41)
(41)
(39) теңдіктен (41) айыра отырып (40) есепке ала отырып:
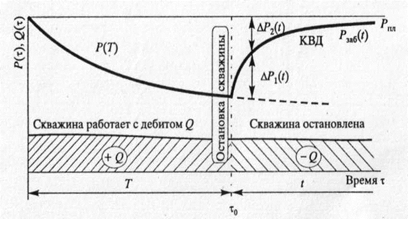 |
Сур. 9. Стационарлық емес жұмыс режимінде ұңғыны зерттеу
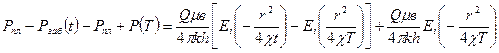 (42)
(42)
немесе:
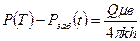
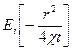 (43)
(43)
Алынған санды (-1) минус бірлікке көбейтіп нәтижесінде :
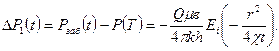 (43)
(43)
немесе:
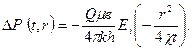 (44)
(44)
(36) теңдіктің шешімі осылай болады. Ол бойынша ұңғы түбі жабық және τ0 (тоқтаған) уақыттағы дебит нөлге тең болады. Уақыт бойынша қысымды өлшеу ұңғы қабырғасында орын алатын болғандықтан:
r=rc=rпр
мұндағы rc, rпр — ұңғының физикалық және келтірілген радиусы.
Енді (44) тендікті былайша қайта жазамыз:
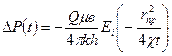 (45)
(45)
(45) теңдік күрделі болып табылғандықтан, мұнда тәжірибелі қолданыс үшін экспоненциялды интегралды функцияның белгілі сандарынкөрсету керек. (45) теңдікті жеңілдетіп шешу үшін экспоненциялды интегралды функцияның Тэйлер қатарымен 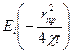 деп шешеміз:
деп шешеміз:
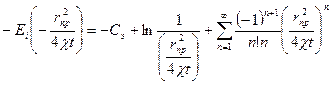 (46)
(46)
мұндағы Сэ — Эйлер коэффиценті ол -0,5772 тең.
Сараптама көрсеткендей үшінші және келесі қатар мүшелерінің снасы аз болғандықтан алғашқы екеуін ғана есепке аламыз. Осылайша (45) теңдікті қайта жазамыз:
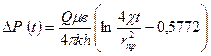 немесе
немесе
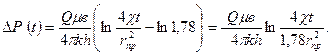
Тиісті қысқартулардан соң соңғы рет былай жазамыз:
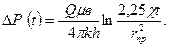 (47)
(47)
Бұл шешімді стационарлық емес мыс кестесінде ұұңғы зерттеу нәтижесінде қысымның төмендеуін қалпына келтіру үшін М.Маскели тапқан. Тағы бір рет естеріңізге салар болсақ, берілген теңдеу қабат жабылып, дебит нөлге теңгерілгенде қолданылады. Ал мұндай жағдайда тәжірибеде кездестіру мүмкін емес.
Дата добавления: 2015-12-08; просмотров: 3835;
