Сандық техниканың логикалық және арифметикалық негіздері

Дәрістің мазмұны:сандық техниканың негізгі ұғымдары мен анықтамаларын еңгізу, арифметика және екілік сандарды кодтау, логика алгебрасының негіздері.

Дәріс мақсаты:сандық техниканың негізгі ұғымдары мен анықтамаларымен танысу, бір санау жүйесінен екінші санау жүйесіне аударудың және екілік арифметиканың негізгі ережелерін меңгеру, екілік сандарды кодтау тәсілдері және аксиомаларды зерттеу, логика алгебрасының негізгі заңдары мен ережелері.

Хабарлама немесе сигнал деп кейбір материалдық тұрғыда жүзеге асырылған ақпарат. Өзгеретін шама (функция) уақыттың нақты мәндерінде орын алуы мүмкін кезде, сигналдар аналогты (үздіксіз) немесе дискретті (сандық) болуы мүмкін. Сандық сигналдар тек 1 және 0 сандарының тізбегінен тұрады. Оларды логикалық деп атайды. Себебі осындай екілік сигналдармен жұмыс жасау ережелерін бекітетін, логика алгебрасы деп аталатын, математиканың бөлімі бар. Сандық сигналдарды өңдеу әдістері және сәйкес келетін құралдар мен жүйелер сандық немесе логикалық деп аталады. Сигналдарды екі түрде көрсетуге болады: потенциалды және импульсты. Бірінщі жағдайда ең үлкен физикалық шама, мысалы, кернеуге логикалық 1 сәйкес келеді, ал ең кіші шамаға – логикалық 0 (оң логика), егер керісінше болса, онда теріс логика орын алады. Екінші жағдайда белгілі бір уақытта импульстің пайда болуы логикалық 1 cәйкес келеді, ал оның болмауы – логикалық 0-ге. Ең көп тараған сандық құралдар - сандық сигналдарды потенциалды түрде көрсетуді қолданатын, әсіресе оң логиканы, сандық микросұлбалар түрінде жүзеге асырылған сандық құралдар.

Сандық техника екілік санау жүйесін қолданады, себебі тек екілік түрде көрсетілген сандарды өңдейді. Бірақ екілік сандарды микропроцессорлық техникада қысқа түрде жазу үшін сегіздік және он алтылық санау жүйелерін қолданады.

Санау жүйесі – бұл сандарды сандық символдармен жазу тәсілі. Санау жүйелерін позициялы және позициялы емес деп бөледі. Позициялы емес санау жүйесінде символдың мағынасы, оның санның ішіндегі орнына байланысты емес, ал позициялы санау жүйесінде байланысты.

Кез келген санды барлық санау жүйелерінде келесі полином түрінде жазуға болады

,

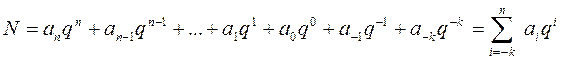Мұнда, q – санау жүйесінің негізі; 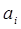- негіздің дәрежелеріндегі коэффициенттер ( 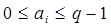); 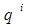- санның разрядтарының салмақтары. Екілік санау жүйесінде q = 2 және екі коэффициент қолданылады (1 и 0). 101101,101 екілік санын келесі полином ретінде көрсетуге болады: .

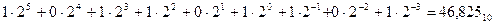Екілік арифметика өте жеңіл. Сандық құрылғыларда қолданылатын негізгі арифметикалық операция қосу болып табылады, себебі алуды алынатын санның таңбасын өзгерте отырып қосындыға ауыстырса болады, ал көбейту мен бөлуді – қосу мен алу операцияларына және кейбір логикалық амалдарға. Екілік сандарды арифметикалық қосу немесе алу кезінде екі логикалық 1 бір разрядта орналаса алмайтынын, яғни олар көрші жоғарғы разрядқа бір логикалық 1 ретінде көшетінін есте сақтау қажет.

Сегіздік санау жүйесінде q = 8 және сегіз коэффициент қолданылады (0,1,2,3,4,5,6,7). 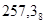сегіздік санды келесі полином түрінде көрсетсе болады .

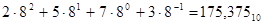Он алтылық санақ жүйесінде q = 16 және он алты коэффициент қолданылады ( 0-ден 9-ға дейінгі сандар және латын алфавитінің алғашқы әріптері). 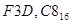Он алтылық санды келесі полином ретінде көрсетуге болады .

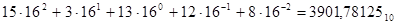Бөлшек санды ондық санау жүйесінен басқа санау жүйесіне аудару екі этаптан тұрады:

1) санның бүтін бөлігі, оны жүйенің негізіне қалдық қалғанша бөлу арқылы аударылады, қалдық жүйенің негізінен үлкен болуы қажет және шыққан сан оңнан солға қарай жазылады;

2) бөлшек бөлігі, оны санау жүйесінің негізіне көбейтіп, үтірден кейін қалдық қалмағанша немесе берілген дәлдік дәрежесіне жеткізу арқылы аударылады. Шыққан сан үтірдің сол жағынан жоғарыдан төмен қарай жазылады. 1-суретте 45,75 ондық санының екілік санау жүйесіне аудару мысалы көрсетілген.

1) 45 2 2) 0,75

1 22 2 2

0112

1 5 2 1,50

1 2 2 2

0 1 1,00

Жауабы: 45,75₁₀ = 101101,11₂

1-сурет — ондық санау жүйесінен екілік санау жүйесіне аудару мысалы

Кері аудару үшін бар болғаны екілік санның бірлік разрядтарының салмақтарын қосу қажет .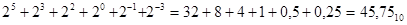

1-кестеде өсу ретімен орналасқан шынайы ондық сандар қатары көрсетілген, олардың әрқайсысына екілік эквивалент сәйкес келеді.

1-кесте

0

1-кесте жалғасы

9								∙∙∙
								∙∙∙

Осы ондық сандарды кодтау әдісінің кемшіліктері:

а) ондық сандардың бірегейлік диапазонын үлкейту үшін құрылғылардың разрядтылығын үлкейту қажет;

ә) шынайы кодтан ондық жүйеге өтуді жузеге асыру техникалық қиын;

Екілік-ондық кодтау жүйесінде бұл кемшіліктер жоқ, өйткені 0-ден 9-ға дейінгі әр ондық санға тетрада түрінде екілік эквивалент береді, яғни төртразрядты екілік сан. Мысалы, осындай кодтау әдісінде 1-кестеге сәйкес 37 санын 0011 0111 түрінде көрсетуге болады. Осыған орай, екілік-ондық кодтау кезінде ондық сандарды екілік түрде көрсету арқылы ондық санау жүйесі сақталады.

Алгебра логикасы сандық құрылғылар жұмысының анализі мен синтезінің математикалық база рөлін атқарады. Оның негізі үш логикалық функция болып табылады: логикалық қосу (дизъюнкция), логикалық көбейту (конъюнкция) және логикалық терістеу (инверсия). 2-суретте НЕМЕСЕ, ЖӘНЕ, ЕМЕС логикалық элементтері және сәйкесінше жүзеге асыратын функциялар көрсетілген.

НЕМЕСЕ ЖӘНЕ ЕМЕС

			х			Y

∙ ∙

∙ ∙

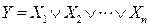
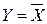
2-сурет – Негізгі базистің логикалық элементтері

Егер НЕМЕСЕ логикалық элементінің кем дегенде бір кірісіне логикалық 1 келсе, кірістік екілік айнымалылардың логикалық қосындысынан шығысы логикалық 1 тең болады. Егер барлық кірістеріне логикалық 0 берілсе, шығысында логикалық 0 болады. Екілік айнымалылардың логикалық көбейтіндісі кезінде әрдайым шығысы логикалық 0 тең, егер ЖӘНЕ логикалық элементінің кем дегенде бір кірісіне логикалық 0 келетін болса. Егер барлық кірістеріне логикалық 1 келетін болса, шығысында логикалық 1 болады. Логикалық терістеу кезінде ЕМЕС логикалық элементінің шығысы әрдайым екілік мағынасының кірісін инверттейді. Іс жүзінде НЕМЕСЕ-ЕМЕС, ЖӘНЕ-ЕМЕС логикалық элементтер көп қолданысқа ие. Олар екі логикалық функцияны орындайды: теріс нәтижелі логикалық қосынды және сәйкесінше теріс нәтижелі логикалық көбейту. ЖӘНЕ, НЕМЕСЕ, ЕМЕС логикалық элементтері логикалық құрылғылар құрылысындағы негізгі базисті құрайды.

Логикалық функцияны құрылымдық формула арқылы берсе болады, яғни теңдік арқылы. Теңдіктің сол жағында әріп жазылған, ол логикалық функцияның мәнін береді, ал оң жағында – логикалық өрнек.

Логикалық өрнектің екі формасы бар: жетілген дизюнктивті нормалы форма (ЖДНФ) және жетілген конъюнктивті нормалы форма (ЖКНФ).

ЖДНФ – бұл минтермдердің логикалық қосындысы, логикалық функция бірге тең. Минтерм – бұл терістеумен немесе терістеусіз көрсетілген кіріс айнымалыларының логикалық туындысы.

ЖКНФ – бұл макстермдердің логикалық туындысы, логикаық функция нөлге тең. Макстерм – бұл терістеумен немесе терістеусіз көрсетілген кіріс айнымалыларының логикалық қосындысы.

Сандық құрылғыларды жобалаған кезде құрылымдық формулаларды жиі өзгерту қажеттілігі туындайды. Ол үшін аксиомалар мен алгебра логикасының заңдарынан шығатын байланыстарды қолданады.

Логикалық қосу, көбейту және терістеу ережелерін қоладана отырып, әділдіктерін дәлелдеуге болатын аксиомаларды қарастырайық.

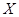- кейбір логикалық айнымалы болсын, онда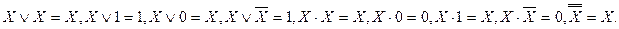

Қосу және көбейту логикалық операциялары үшін көшіретін және үйлестіретін заңдар әділ болады. Орналастыратын заңның тек бірінші бөлігі (жақшаны ашу ережесі) ғана кәдімгі алгебраға сәйкес келеді, ал екінші бөлігі (жақшаға алу ережесі) тек логика алгебрасында ғана орын алады.

Құрылымдық формулаларды өзгерту үшін іс жүзінде ең көп қолданатын логика алгебрасының кейбір ережелерін қарастырайық. 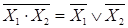және 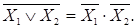де Морган ережесі. Бұл ереже логикалық көбейтуді қосумен ауыстыруға және керісінше жасауға мүмкіндік береді. 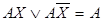және 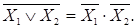жабыстыру ережесі. Жабыстыру ережесіне Карно карталарының графикалық әдістері мен логикалық функцияларды минимизациялау үшін арналған Вейч диаграммалары негізделген.