ПРИ ПЕРЕМЕННОЙ НАГРУЗКЕ

Принято различать нагрузочные диаграммы механизма и электропривода. Под нагрузочной диаграммой механизма понимают зависимость момента сопротивления механизма М_м или мощности Р_м от времени. Вместе с нагрузочной диаграммой механизма дается или рассчитывается скоростная диаграмма ω_м(t).

Для электропривода нагрузочная диаграмма (М = f(t) или Р = f(t)) более сложна, так как она определяется не только статическими режимами работы, но и переходными процессами электропривода. Переходные процессы в системе электропривода оказывают заметное влияние на момент, развиваемый двигателем, и соответственно на зависимость М(t). К ним прежде всего относятся: включение двигателя в сеть и его отключение, изменение параметров подводимого напряжения, главных цепей и цепей возбуждения и т.п. В таких случаях dω/dt ≠ 0. Поэтому при построении нагрузочной диаграммы электропривода М(t) следует пользоваться уравнением движения.

Для электроприводов, работающих длительно с постоянной нагрузкой и скоростью, можно не учитывать потери энергии в переходных процессах, т.е. не учитывать динамическую составляющую момента двигателя и считать М(t) = М_с = const и Р(t) = Р_с = const.

Формулы для расчета мощности и момента производственных механизмов определяются спецификой их работы и относительно просты. Например, мощность насоса зависит от массы перекачиваемой жидкости и скорости ее движения, мощность подъемного механизма определяется весом поднимаемого груза и скоростью подъема, мощность двигателя шпинделя металлорежущего станка – усилием резания и скоростью резания и т.д.

Более сложным представляется построение нагрузочной диаграммы электропривода, когда скорость, ускорение и другие показатели системы не остаются постоянными в процессе работы механизма. В качестве примера рассмотрим построение нагрузочной диаграммы лифтадля рабочего участка, на котором кабина лифта разгоняется до определенной скорости, движется некоторое время с постоянной скоростью, а затем затормаживается.

По соответствующим формулам можно рассчитать статическую нагрузку лифта М_с(t). Заданными для кабины лифта являются скорость движения кабины ω, а также максимальные значения величин dω/dt и d²ω/dt², которые обусловливаются соответствующими нормами.

Нагрузочная диаграмма лифта строится в виде графика (рис. 13.1), состоящего из семи участков. Первым строится участок 4-го графика, на котором dω/dt = const. Затем можно построить участки 2 и 6, на которых постоянными являются ускорение и замедление, а скорость увеличивается и уменьшается по линейному закону. Участки 1, 3, 5, 7 характеризуются линейным изменением ускорения (замедления), когда вторая производная от скорости по времени (рывок) остается постоянной, обусловленной нормами, а скорость изменяется по параболическому закону.

Рис. 13.1. К построению нагрузочной диаграммы ЭП пассажирского лифта

По известному моменту инерции J системы электропривода лиф-та можно построить график J dω/dt = f(t), так как dω/dt известна.

Таким образом, имеются все данные для построения графика М(t):

М(t) = М_с + J dω/dt.

На основании графиков М(t) и ω(t) можно построить зависимость Р(t) = М(t)∙ω(t) и далее перейти к выбору электродвигателя по мощности, если по данной методике будут построены нагрузочные графики и для других участков движения кабины лифта.

Методы расчета мощности электродвигателя при переменной нагрузке. В электроприводах, у которых мощность на валу электродвигателя изменяется по определенному нагрузочному графику (рис. 13.2), электродвигатель сначала выбирают по наибольшей мощности этого графика с учетом его перегрузки, а затем выбранный электродвигатель проверяют по нагреву. Примерами электропривода с переменной нагрузкой на валу электродвигателя являются электроприводы многооперационных станков, кулачковых автоматов и др. Форма нагрузочного графика зависит от обрабатываемой детали, мощности и продолжительности отдельных переходов цикла обработки детали. При этом электродвигатель вращается непрерывно почти с постоянной скоростью, хоть его механическая характеристика имеет большую жесткость.

Рис. 13.2. Нагрузочный график при переменной нагрузке

Для проверки выбранного электродвигателя по нагреву при переменной нагрузке существуют следующие четыре метода:

1) метод эквивалентного тока I_э;

2) метод эквивалентного момента М_э;

3) метод эквивалентной мощности Р_э;

4) метод средних (эквивалентных) потерь.

Рассмотрим эти методы.

Метод средних (эквивалентных) потерь. При переменной нагрузке (в станкостроении и других областях) наиболее часто используют обычные электродвигатели, предназначенные для длительного режима работы с постоянной нагрузкой. Поэтому электродвигатель выбирают на такую постоянную мощность Р_э длительного режима работы, при которой в электродвигателе выделяется столько же тепла за время цикла работы t_ц, сколько и при работе при переменной нагрузке:

Q_э × t_ц = ∑(Q_i ×∙t_i) или ∆P_э × t_{ц =} ∑(∆P_i × t_i),

где Q_э – количество тепловой энергии, выделяемой в электродвигателе мощностью Р_э в единицу времени;

∆Р_э – потери мощности в электродвигателе при работе с мощностью Р_э;

∆Р_i – потери мощности в электродвигателе при работе с мощностью Р_i.

Отсюда получаем формулу средних потерь:

∆P_э = ∑(∆P_i × t_i) / t_ц. (13.1)

Метод средних (эквивалентных) потерь для проверки электродвигателя по нагреву, предварительно выбранного по перегрузке, основан на использовании этой формулы средних потерь и состоит в следующем:

1.Используя нагрузочный график, определяют:

∆P_i = P_i / η_i – P_i,

где η_i – КПД электродвигателя при работе с мощностью P_i.

В достаточно подробных технических данных АД приводят значения КПД при нагрузках 1/4, 2/4, 3/4, 4/4 и 5/4 от Р_н. По этим данным строят график η = f (Р), из которого определяют значения η_i.

Для приближенных расчетов (и при отсутствии данных для построения графика η = f (Р)) можно использовать формулу

.

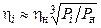2.Вычисляют ∆Р_э по формуле (13.1) и проверяют выполнение условия ∆Р_э ≤ ∆Р_н.

Если это условие не выполняется, берут следующий по номинальной мощности электродвигатель из каталога и т.д. до выполнения данного условия.

Метод эквивалентного тока. Если в формуле (13.1) потери мощности разделить на постоянные и переменные, пропорциональные квадрату тока нагрузки I², получим

∆Р_пост + b∙I_э² = ∑((∆Р_пост + b∙I_i² ) × t_i) / t_ц, (13.2)

где b – величина, постоянная для конкретного двигателя.

Так как ∆Р_пост × t_ц = ∆Р_пост × ∑ t_i, то после преобразований и решения (13.2) относительно I_э получим

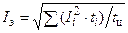. (13.3)

Эта формула соответствует нагрузочному графику (см. рис. 13.2) с прямоугольными участками. Если нагрузочный график I = f(t) содержит треугольные и трапецеидальные участки (рис. 13.3), в формулу (13.3) вместо I₁ и I₅ следует подставлять

; .

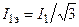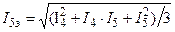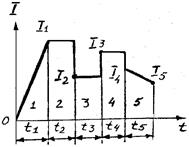
Рис. 13.3. Нагрузочный график I = f (t)

Метод эквивалентного тока основан на использовании формулы (13.3) при проверке электродвигателя по нагреву и состоит в следующем:

1.Рассчитывают I_э по (13.3), используя нагрузочный график I = f(t).

2.По каталогу (зная предварительно род тока, напряжение, скорость вращения и другие данные) выбирают электродвигатель с номинальным током I_н ≥ I_э.

Данный метод применим к электродвигателю любого типа.

Метод эквивалентного момента. Для ДПТ НВ и АД метод эквивалентного тока можно заменить методом эквивалентного момента, использующего формулу эквивалентного момента

,

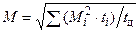так как для ДПТ при Ф = const ток пропорционален моменту, а для АД при небольших значениях скольжения (на рабочем участке) момент можно считать примерно пропорциональным току.

Метод эквивалентной мощности. Если скорость вращения электродвигателя во время работы изменяется незначительно, что характерно для электродвигателей с жесткими механическими характеристиками, то мощность примерно пропорциональна моменту. Тогда можно пользоваться методом эквивалентной мощности, использующим формулу эквивалентной мощности,

.

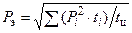Эта формула более удобна, чем формула средних потерь, в которой необходимы дополнительные вычисления КПД η_i.

Данный метод используют также и при небольшом числе пусковых процессов (до 20 в час), пренебрегая их влиянием на нагрев электродвигателя.