Дифференциальное уравнение теплопроводности
При решении задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности.
Температурное поле – совокупность значений температур во всех точках рассматриваемого пространства для каждого момента времени 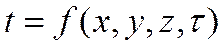 .
.
Для упрощения вывода этого дифференциального уравнения сделаны следующие допущения:
– тело изотропно;
– физические параметры постоянны;
– деформация рассматриваемого объема, связанная с изменением температуры, является очень малой величиной по сравнению с самим объемом;
– внутренние источники теплоты в теле 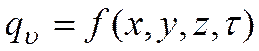 распределены равномерно.
распределены равномерно.
В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии в формулировке:
количество теплоты dQ, введенное в элементарный объем извне за время dτ теплопроводностью, а также от внутренних источников, равно изменению внутренней энергии или энтальпии вещества (в зависимости от рассмотрения изохорного или изобарного процесса), содержащегося в элементарном объеме.
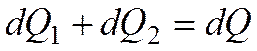 (*)
(*)
где dQ1 – количество теплоты, Дж, введенное в элементарный объем теплопроводностью за время dτ;
dQ2 – количество теплоты, Дж, которое за время dτ выделилось в элементарном объем 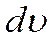 за счет внутренних источников;
за счет внутренних источников;
dQ – изменение внутренней энергии или энтальпии вещества, содержащегося в элементарном объеме 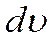 , за время dτ.
, за время dτ.
Для нахождения составляющих выделим в теле элементарный параллелепипед со сторонами dx, dy, dz. Параллелепипед расположен так, чтобы его грани были параллельны соответствующим координатным плоскостям.
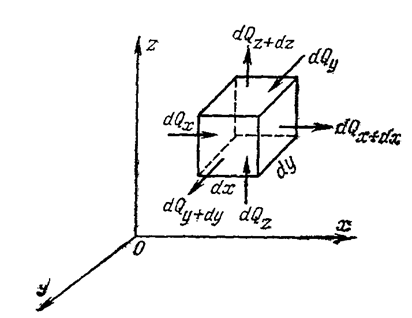
Количество теплоты, которое подводится к граням элементарного объема за время dτ в направлении осей Оx, Оy, Оz обозначим соответственно dQx, dQy, dQz.
 Количество теплоты, которое будет отводиться через противоположные грани в тех же направлениях, обозначим соответственно dQx+dx, dQy+dy, dQz+dz.
Количество теплоты, которое будет отводиться через противоположные грани в тех же направлениях, обозначим соответственно dQx+dx, dQy+dy, dQz+dz.
Количество теплоты, подведенное к грани dydz=dF в направлении оси Ох за время dτ, составляет 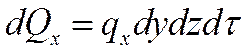 ,
,
где qx – проекция плотности теплового потока на направление нормали к указанной грани.
Количество теплоты, отведенное через противоположную грань элементарного параллелепипеда в направлении оси Ох
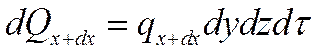 .
.
Разница количеств теплоты, подведенного к элементарному параллелепипеду и отведенного от него за время dτ в направлении оси Ох
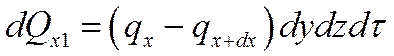
Функция 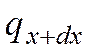 является непрерывной в рассматриваемом интервале dx и может быть разложена в ряд Тейлора
является непрерывной в рассматриваемом интервале dx и может быть разложена в ряд Тейлора
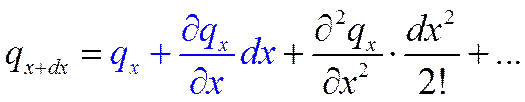
Если ограничиться двумя первыми членами ряда:
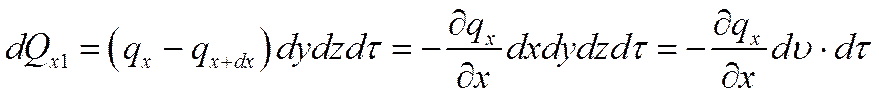
Аналогично можно найти количество теплоты, подводимое к элементарному объему в направлениях двух других координатных осей Oy и Oz.
Количество теплоты dQ, подводимое теплопроводностью к рассматриваемому объему, будет равно
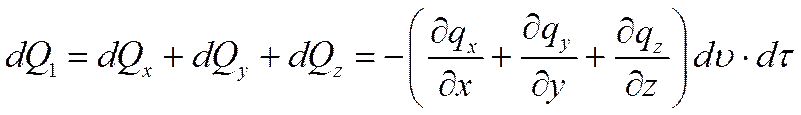
Обозначим через 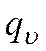 , Вт/м3, количество теплоты, выделяемое внутренними источниками в единице объема в единицу времени.
, Вт/м3, количество теплоты, выделяемое внутренними источниками в единице объема в единицу времени.
Тогда 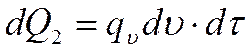
Третья составляющая уравнения (*) найдется в зависимости от характера термодинамического процесса изменения системы.
В случае рассмотрения изохорного процесса вся теплота, подведенная к элементарному объему, уйдет на изменения внутренней энергии вещества, заключенного в этом объеме, т.е.
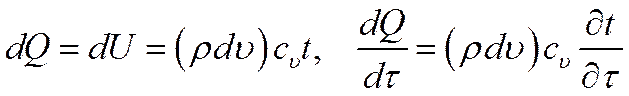
где 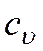 – изохорная теплоемкость единицы массы, Дж/(кг·К);
– изохорная теплоемкость единицы массы, Дж/(кг·К);
ρ – плотность вещества, кг/м3.
Подставляя полученные выражения в уравнение (*), получим
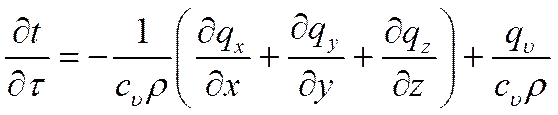 ,
,
Проекции вектора плотности теплового потока на координатные оси Ох, Оу, Оz определяются законом Фурье:
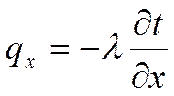 ;
; 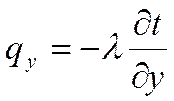 ;
; 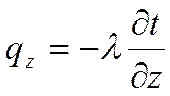 .
.
где λ – коэффициент теплопроводности (физический параметр вещества, характеризующий способность проводить теплоту), Вт/(м∙°С).
Подставляя полученные выражения проекций вектора плотности теплового потока в уравнение (*), опуская индекс при с, ипринимая теплофизические характеристики постоянными, получим
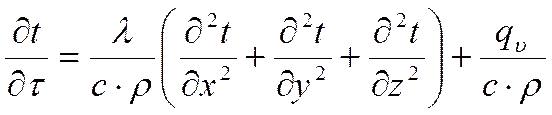 (***)
(***)
Выражение (***) называется дифференциальным уравнением теплопроводности. Оно устанавливает связь между временнЫм и пространственным изменением температуры в любой точке тела.
Можно обозначить
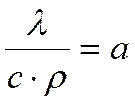 и
и 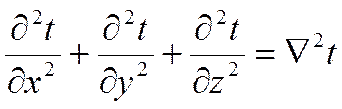
Тогда выражение (***) имеет вид:
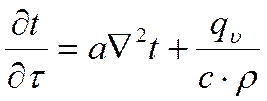
Выражение (***) в цилиндрической системе координат:

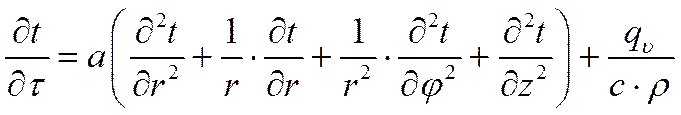
где r – радиус-вектор;
φ – полярный угол;
z – аппликата.
Коэффициент пропорциональности а, м2/с, называется коэффициентом температуропроводности и является физическим параметром вещества.
Он характеризует скорость изменения температуры, т.е. является мерой теплоинерционных свойств тела. Поэтому при прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает бόльшим коэффициентом температуропроводности.
Коэффициент температуропроводности зависит от природы вещества.
Например, жидкости и газы обладают большой тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности.
Металлы обладают малой тепловой инерционностью, т.к. они имеют большой коэффициент температуропроводности.
Если система тел не содержит внутренних источников теплоты (qυ=0), то
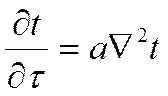
Если имеются внутренние источники теплоты, но температурное поле соответствует стационарному состоянию, т.е. 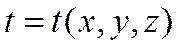 , то
, то
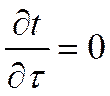
При рассмотрении изобарного процесса вся теплота, подведенная к объему, уйдет на изменение энтальпии вещества, заключенного в этом объеме:
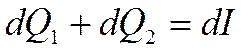 (**)
(**)
Если рассматривать энтальпию единицы объема как 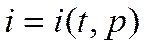 , то
, то
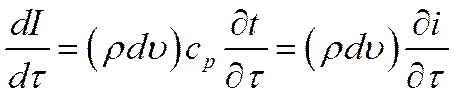
где сp – изобарная теплоемкость единицы массы, Дж/(кг·К).
В итоге (**) имеет вид:
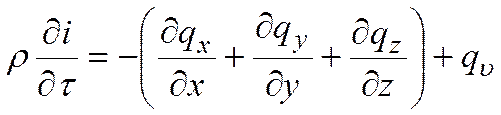
| <== предыдущая лекция | | | следующая лекция ==> |
| СПОСОБЫ ПЕРЕНОСА ТЕПЛОТЫ | | | Условия однозначности для процессов теплопроводности. Дифференциальное уравнение теплопроводности описывает явление теплопроводности в самом общем виде |
Дата добавления: 2016-02-09; просмотров: 5387;
