Вплив речовини на поширення світла обумовлений взаємодією світла з атомами і молекулами, з яких складається речовина

Ця взаємодія призводить до зміни швидкості світла υ, а отже, визначає і значення показника заломлення п = 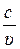, де с – швидкість світла у вакуумі.

Основи теорії дисперсії можуть бути одержані, якщо розглядати взаємодію світлових хвиль із зарядженими частинками (електронами і позитивними ядрами), що входять до складу атомів і молекул. При цьому передбачається, що заряджені частинки в атомах і молекулах утримуються біля своїх положень рівноваги квазіпружними силами. Таким чином, кожен атом або молекула мають певну власну частоту коливань w₀. Під впливом падаючої світлової хвилі заряджені частинки в атомах і молекулах здійснюють вимушені коливання з частотою, співпадаючою з частотою падаючої хвилі w.

Первинна електромагнітна (світлова) хвиля, поширюючись через речовину зі швидкістю с, викликає вимушені коливання частинок. Завдяки цьому біля кожної частинки виникнуть вторинні хвилі. Амплітуда і фаза цих вторинних хвиль визначаються амплітудою і фазою вимушених коливань частинок; останні ж залежать від співвідношення між частотою падаючої хвилі w і частотою власних коливань w₀.

Таким чином, у речовині поширюються хвиля первинна і вторинна. Фаза вторинних коливань запізнюється відносно первинних, і тому виникає деяка різниця фаз. (Запізнення відбувається внаслідок того, що самі ці заряджені молекули мають деяку інерцію). Швидкість сумарної хвилі менша за швидкість первинної хвилі, тобто має місце показник заломлення.

При вивченні гармонійних коливань ми встановили, що періодична вимушуючи сила з частотою w викликає вимушене коливання з амплітудою

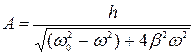4.19

і фазою α, яка визначається рівністю:

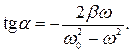4.20

Тут h — константа, β – коефіцієнт, що характеризує загасання коливань системи. При малому значенні коефіцієнта β, роль загасання помітна лише для частот вимушуючої сили w, які близькі до частот власних коливань w₀. Тому при слабкому загасанні для всіх частот w, не дуже близьких до w₀, можна приблизно написати:

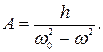4.21

Амплітуда і фаза вимушених коливань залежать від співвідношення частот w₀ і w. Поблизу резонансу амплітуда А велика. При w<<w₀ амплітуда А значно менше і із зменшенням w прямує до постійної границі, не рівної нулеві. Якщо
w >> w_0, то амплітуда А вимушених коливань зменшується до нуля із зростанням частоти w. Фаза вимушених коливань змінюється від 0 до –π при зміні w від нуля до частот, які багато більше w₀. Біля резонансу (при малому загасанні) фаза близька до – 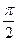. Ті ж висновки відносяться до амплітуди і фази вторинних хвиль.

Вторинні хвилі, складаючись із первинною, утворюють результуючу хвилю з амплітудою і фазою, відмінними від амплітуди і фази первинних хвиль. Це призводить до того, що хвиля проходить через речовину з фазовою швидкістю, відмінною від швидкості, з якою вона розповсюджувалася б у порожнечі. Відмінність у швидкостях буде тим більша, чим сильніші вимушені коливання частинок.

Звідси витікає, що світло (електромагнітні хвилі), частота якого набагато менше частот власних коливань атомів або молекул, проходить через речовину з швидкістю, практично не залежною від частоти, але відмінною від швидкості світла у вакуумі (оскільки А ≈ const ≠ 0).

Для світла дуже великої частоти, що помітно перевищує частоти власних коливань атомів, амплітуда вторинних хвиль близька до нуля, він проходить через речовину з швидкістю, близькою до швидкості світла у вакуумі. Показник заломлення для таких речовин близький до одиниці. В обох розглянутих випадках, як випливає з теорії, поглинання світла незначне. При значеннях частот, w близьких до w_0, швидкість світла в речовині починає дуже відрізнятися від його швидкості у вакуумі. Завдяки цьому і показник заломлення дуже відрізняється при цих частотах від одиниці: при w<w₀ він виявляється «аномально» великим; при w>w₀ — «аномально» малим. Крім того, при w близькому до w_0, в результаті великих амплітуд вимушених коливань велике і поглинання.

Речовина, що складається з атомів або молекул із певним набором частот власних коливань w_0і, дасть у спектрі вузькі лінії (лінії поглинання). Показник заломлення виявиться постійним в областях, далеких від поглинання, і швидко мінятиметься з частотою і дуже відрізнятиметься від одиниці поблизу кожної лінії поглинання, де взаємодія світла з речовиною велика.

ІІ. За електромагнітною теорією світла показник заломлення визначається рівністю

.

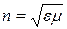Для всіх прозорих діелектриків магнітна проникність μпрактично рівна одиниці, тому маємо:

.

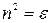Діелектричні властивості речовини обумовлені її поляризацією, яка виникає у зв’язку зі зміщенням заряджених часток у атомі або молекулі, відносно положення рівноваги внаслідок дії електромагнітних хвиль.

При цьому значення діелектричної постійної ε не буде бути постійним. Для швидко змінних електричних полів, які мають місце в світловій хвилі, ці зміни виражаються знайденою нами амплітудою. Тому, як показує теорія, квадрат коефіцієнта заломлення n² виражається наступною дисперсійною формулою:

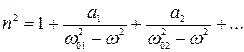4.22

де w₀₁, w₀₂, … — частоти власних коливань атомів або молекул, а₁, а₂…— деякі константи. Оскільки довжина хвилі λ пов’язана з циклічною частотою співвідношенням:

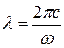, 4.23

де с — швидкість світла у вакуумі, то формулі (4.22) можна також надати вигляду:

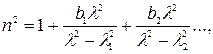4.24

де b₁, b₂ ... – нові константи, а λ₁, λ₂, ... – довжини хвиль, відповідні резонансу. Формула (4.24) дає значення показника заломлення в проміжку між лініями поглинання. Якщо обмежитися у формулі (4.24) двома членами (речовина з двома власними частотами коливань), то вийде залежність п²–1від λ,зображена

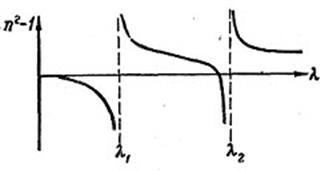
Рис. 4.36. Залежність коефіцієнта заломлення n від довжини

хвилі λ поблизу двох ліній поглинання λ₁ і λ₂

на рисунку 4.36. Пунктирні лінії показують положення ліній поглинання речовини λ₁ і λ₂. Поблизу ліній поглинання крива дисперсії круто згинається. У кожної лінії поглинання з боку малих довжин хвиль (λ < λ_і) коефіцієнт заломлення n приймаємалі значення, а з боку великих довжин хвиль (λ > λ_і) — вельми великі значення. За формулою (4.24) для довжини хвилі, меншої і дуже близької до однієї з λ,для п² вийдуть від’ємні значення, що дає уявні значення для n. Це відбувається через те, що не врахований коефіцієнт загасання β. Тому формулою (4.24) можна користуватися лише в областях, де β дуже мале. Далеко від ліній поглинання значення показника заломлення п наближаєтьсядо постійних величин.

Загальний хід дисперсії, зображений на рисунку, з характерними вигинами біля ліній поглинання має назву «аномальної» дисперсії. Насправді в цьому ході немає нічого «аномального», навпаки, він є типовим ходом, що відповідає фізичній суті явища. Область монотонної зміни показника заломлення між двома лініями поглинання передає характер дисперсії прозорих речовин і має назву нормальної дисперсії.