Комбінаційне розсіювання світла

Суттєвим методом вивчення властивостей молекул є комбінаційне розсіювання світла, тобто таке розсіювання, при якому змінюється частота. Релеєвське розсіювання спостерігається, якщо розсіюючі частинки не здійснюють таких коливань, які призводять до періодичного змінення амплітуди розсіяних променів. У останньому випадку світло буде модульованим. Якщо частота власних коливань розсіюючої частинки , то . Л.І.Мандельштам вказав, що такого роду модуляції світла можуть спостерігатися при розсіюванні променів від згустків, що виникають при тепловому русі в кристалах. В кристалічній решітці тепловий рух призводить до створення стоячих хвиль. Завдяки цьому в певних місцях у кристалі періодично виникають згущення і розрідження, які викликають модульоване розсіювання світла. Зміна первинної частоти дорівнює ~ 1/1000 процента (Грос). Друга причина заключається в коливанні іонів, які входять до складу молекул. Виникають промені з частотою , де – частота власних коливань іонів у молекулі ( ~10¹²с^-1). Якщо молекула має декілька власних частот коливань , , , ..., то у розсіяному світлі повинні з’явитися всі „комбінаційні” частоти: ; ; 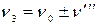. Звідси і назва – комбінаційне розсіювання світла. Воно виявлено експериментально у 1928 році в Московському університеті Л.І.Мандельштамом і Г.С.Ландсбергом, які вивчали спектральний склад променів, розсіяних від кварцу (рис. 4.47). Розсіювання від рідин вивчалося індусами К.Кришнаном і Ч.Раманом.

Схема досліду Мандельштама і Ландсберга

Рис. 4.47

S – ртутна дуга;

– релеївська лінія завжди присутня, вона оточена „червоними” зміщеними в бік збільшення довжин хвиль і „фіолетовими” супутниками, зміщеними в бік зменшення довжин хвиль, які розміщені симетрично.

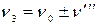; ; , при чому , , не залежать від , а характерні для даної розсіюваючої речовини. Якщо первинний пучок має декілька „ліній”, то біля кожної з’являються супутники. „фіолетові” супутники слабкіші „червоних”. Із підвищенням температури інтенсивність „фіолетових” супутників значно підвищується, інтенсивність „червоних” не залежить від температури.

Комбінаційне розсіювання має квантовий характер. Із точки зору квантової механіки випромінювання і поглинання коливальних частот пов’язані з переходом молекули з одного квантового (енергетичного) стану в інший (рис. 4.48). Нехай молекула може знаходитись у ряді коливальних енергетичних станів Е₀, Е₁, … , Е_і . Припустимо, що нормальний стан Е_0. В результаті взаємодії молекули з фотоном енергії , молекула може бути переведеною в більш високий енергетичний стан Е_і.

Рис. 4.48 а) Рис. 4.48 б)

На цей перехід витрачається енергія . Енергія фотону зменшується на величину .

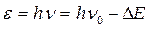; тобто ;

з’являється “червоний” супутник. Появу “фіолетового” супутника можна пояснити якщо припустити, що частина молекул спочатку знаходяться у збудженому стані Е_і. Така молекула віддасть падаючому фотону енергію і виникне розсіяний фотон з енергією , тобто для “фіолетового” супутника. . Зрозуміло, що збуджених молекул менше, ніж нормальних, тому інтенсивність “фіолетових” супутників менша, ніж “червоних”. Із підвищенням температури число збуджених молекул збільшується й інтенсивність фіолетових супутників збільшується. Число молекул у нормальному стані мало зменшується з підвищенням температури, тому інтенсивність червоних супутників помітно не змінюється.

Комбінаційне розсіювання може виникнути і при обміні енергією між фотонами й обертальними енергетичними станами молекули. Ці енергії малі й супутники, які відповідають їм, знаходяться ближче до основної лінії. Комбінаційне розсіювання є важливим методом вивчення власних частот коливань у складних багатоатомних молекулах, особливо в молекулах органічних з’єднань. У наш час широко використовується метод молекулярного спектрального аналізу.

§4.2. Практичні заняття

Практичне заняття № 12. Тема: Поляризація світла.

План

1.Поляризація світла при відбиванні від діелектрика.

2.Поляризація при заломленні.

3.Закон Брюстера.

4.Подвійне променезаломлення. Закон Малюса.

Основні формули:

1) 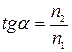– закон Брюстера. 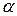– кут повної поляризації світла. – відносний показник заломлення другого середовища відносно першого.

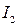2) – закон Малюса, де – інтенсивність світла, що виходить із аналізатора, 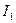– інтенсивність світла, що виходить із поляризатора і потрапляє на аналізатор. , де – інтенсивність світла, яке падає на систему, тобто інтенсивність природного світла. Поляризатор розділяє це світло на звичайне та незвичайне, інтенсивність яких однакова. Тому закон Малюса можна записати і так 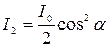, де 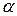– кут між головними площинами поляризатора і аналізатора.

Приклади розв’язування задач

Задача № 1

Чому дорівнює показник заломлення скла, якщо при відбиванні від нього світла відбитий промінь буде повністю поляризований при куті заломлення ?

Дано: Аналіз та розв’язок

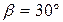
За законом Брюстера за законом заломлення. , тобто кут .

.

Відповідь: , а також ми показали, що при повній поляризації кут між відбитим і заломленим променями рівний , тобто вони взаємно перпендикулярні.

Задача № 2

В скільки разів ослаблюється світло при проходженні через два ніколі, площини поляризації яких створюють між собою кут 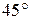, якщо кожен ніколь поглинає 5% світла, що проходить крізь нього.

Дано: Аналіз та розв’язок

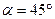
Без поглинання закон Малюса запишемо у вигляді: 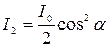. З урахуванням поглинання: . Тобто

.

Відповідь: інтенсивність зменшиться в 4,43 рази.

Задача № 3

Якщо між двома схрещеними поляроїдами розмістити третій, оптична вісь якого складає кут 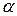з оптичною віссю аналізатора, то поле зору посвітлішає. Знайти інтенсивність пройденого світла. Втратами світла на відбиття та поглинання знехтувати.

Дано: Аналіз та розв’язок

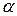
І₀ – інтенсивність природного світла;

І₃ – інтенсивність світла, що вийшло із системи поляроідів

У незвичайного променя, що пройшов крізь поляризатор, вектор напруженості електричного поля буде , а проекцією вектора на оптичну вісь третього поляроїда буде напруженість електричного поля променя, який пройшов третій поляроїд . Аналогічно це проекція на оптичну вісь аналізатора, тобто напруженість електричного поля променя, який пройшов крізь аналізатор . Підставивши , отримаємо = . Інтенсивність хвилі пропорційна квадрату вектора напруженості: . Враховуючи, що аналізатор пропустив тільки незвичайний промінь, інтенсивність 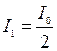, тоді

.

Відповідь: .

Задачі для самостійного розв'язування та домашнього завдання:

12.1. Знайти кут повної поляризації при відбиванні світла від скла, показник заломлення якого 1,57.

12.2. Граничний кут повного внутрішньго відбивання для деякої речовини дорівнює 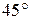. Чому дорівнює для цієї речовини кут повної поляризації?

12.3. Під яким кутом до горизонту повинно знаходитись Сонце, щоб його промені відбивання від поверхні озера були б найбільш поляризовані?

12.4. Промінь світла проходить крізь рідину, налиту в скляний ( ) сосуд, і відбивається від дна. Відбитий промінь повністю поляризований при падінні його на дно сосуда під кутом 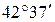. Знайти 1) показник заломлення рідини; 2) під яким кутом повинен падати на дно сосуда промінь світла, який іде в цій рідині, щоб наступило повне внутрішнє відбивання.

12.5. Чому дорівнює кут між головними площинами аналізатора і поляризатора, коли інтенсивність природного світла, яке пройшоло крізь поляризатор та аналізатор, зменшилась у чотири рази? Поглинанням світла нехтувати.

12.6. Природне світло проходить крізь поляризатор та аналізатор, які розташовані так, що кут між головними площинами дорівнює 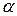. Як поляризатор, так і аналізатор поглинають та відбивають 8% світла, яке на них падає. Сталося так, що інтенсивність променя, який вийшов із аналізатора, дорівнює 9% інтенсивності природного світла, яке падає на поляризатор. Знайти кут .

12.7. Під яким кутом потрібно відбити промінь від кристала кам'яної солі ( 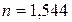), щоб отримати максимальну поляризацію відбитого променя?

12.8. Головні площини двох призм Ніколя створюють між собою кут у . Як зміниться інтенсивність світла, що їх пройшло, коли головні площини поставити під кутом у ?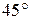

12.9. За допомогою якого простого досліду можна довести, що світлові вектори в природньому світлі орієнтовані сіметрично відносно напряму поширення?

12.10. Природне світло проходить крізь поляризатор та аналізатор. Інтенсивність світла, яке виходить з аналізатора, становить 25% інтенсивності природнього світла. Визначити кут 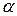між площинами пропускання поляризатора та аналізатора.

12.11. У скільки разів послаблюється інтенсивність світла, що проходить крізь два Ніколі, площини поляризації яких утворюють кут , якщо в кожному Ніколі втрачається 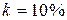падаючого на нього світлового потоку?

12.12. Природне світло падає на систему з трьох послідовно разміщених поляроїдів. Площини пропускання перших двох поляроїдів утворюють кут 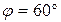, а напрям площини пропускання третього поляроїда збігається з напрямом площини першого. Коефіцієнт пропускання кожного поляроїда . У скільки разів зменьшиться інтенсивність світла після проходження системи?

12.13. Природне світло інтенсивністю проходить крізь поляризатор та аналізатор, головні площини яких утворюють кут . Після проходження системи світло падає на дзеркало і, відбившись, знову проходить крізь неї. Якою буде інтенсивність 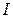світла після його зворотнього проходження?

12.14. Визначити показник заломлення скла , якщо у разі відбивання від нього світлового пучка у повітрі кут максимальної поляризації становить . Як зміниться кут максимальної поляризації, якщо скло занурити у воду?

12.15. Встановити найменше значення кута повної поляризації під час падіння світла з повітря на поверхню речовини, показник заломлення якої .

12.16. Який повинен бути заломлюючий кут скляної призми, щоб кути входу та виходу променя з призми були кутами повної поляризації? Який при такому преломлюючому куті, кут найменьшого відхилення?

Практичне заняття № 13. Тема: Поляризація світла

План:

1.Побудова хвильових поверхонь Гюйгенса та ходу променів, звичайного та незвичайного.

2.Обертання площини поляризації.

3.Інтерференція поляризованих променів.

Основні формули та співвідношення:

1) Коли 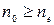, тобто – кристал від’ємний. Коли , тобто – кристал додатній.(см. рис. 1 і 2)

2) 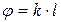, де – кут повороту площини поляризації, – коефіцієнт пропорційності, який залежить від властивостей речовини. – це питоме обертання, кут, на який повертається площина поляризації при проходженні променем товщі кристалу в 1 мм, , тобто залежить від довжини хвилі поляризованого світла.

3) – закон Біо, де – кут повороту площини поляризації, – коефіцієнт, який залежить від роду взятої речовини та від довжини хвилі, – довжина шляху променя в рідині, – концентрація речовини.

4) – рівняння еліпса, який одержується при інтерференції двох променів, поляризованих у взаємно перпендикулярних площинах. Це еліптична поляризація. В загальному випадку одержується еліпс, довільно орієнтований відносно осей та 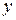. – різница фаз коливань, і –амплітуди коливань звичайного і незвичайного променів.

Задача № 1

Побудувати за Гюйгенсом напрямок заломлених хвиль в одновісному кристалі, додатньому та від’ємному для випадку, коли оптична вісь лежить у площині падіння, паралельно поверхні кристала. Промені падають на кристал нормально.

Аналіз та побудова:

Рис. 1 Рис. 2

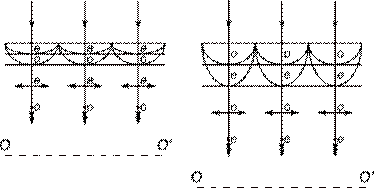
Рис.3 Рис.4

Намалюємо хвильові поверхні для додатнього та від’ємного кристалів. Для додатного кристала . Хвильова поверхня звичайного променя – сферична поверхня, тому що не залежить від напрямку поширення в кристалі, а хвильова поверхня незвичайного променя – еліпсоїд обертання. Тобто хвильові поверхні додатнього променя будуть виглядати як на рис. 1, від’ємного – як на рис. 2.

Намалюємо поверхню поділу повітря-кристал у першому та другому випадках.

Вісь позначена пунктиром. Намалюємо ті частини поверхонь, які знаходяться в кристалі, проведемо огинаючі цих поверхонь і продовжимо промені до точок дотикання. Це і будуть промені, що поширюються в кристаллах: додатній (рис. 3) і від’ємний (рис. 4). Як бачимо, в цьому випадку промені поширюються в одному напрямку, але в додатньому кристалі звичайний промінь випереджує незвичайний, а в від’ємному – навпаки. Площини коливань у першому і другому випадках також змінилися.

Задача № 2

Паралельний пучок світла падає нормально на пластинку ісландського шпату, що вирізана паралельно оптичній вісі. Визначити різницю ходу звичайного та незвичайного променів, які пройшли крізь пластинку. Товщина пластинки 0,03 мм.

Дано: Аналіз та розв’язок:

мм

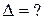
Із умови задачі видно, що кристал ісландського шпата відноситься до від’ємних кристалів, так як . Із попередньої задачі видно, що в такому випадку, як ми маємо в цій задачі, промені в кришталі не розщеплюються, але незвичайний промінь має більшу швидкість і випереджає звичайний. Оптична різниця ходу буде дорівнювати

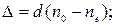
мм нм.

Відповідь: 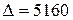нм

Задача № 3

В кювету цукрометра налито 5% розчин цукру, який повертає площину поляризації на 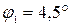. Визначити концентрацію такого розчину цукру, який повертає площину поляризації на .

За законом Біо , де – коефіцієнт, який залежить від властивостей речовини та від довжини хвилі, – довжина шляху променя в розчині цукру, – концентрація цукру. Тобто . Якщо розчин цукру наливають в одну і ту ж кювету, то 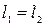. Поділимо вирази, одержимо:

Дано: Аналіз та розв’язок:

, тобто .

Відповідь:

Задача № 4

Знайти найменшу товщину пластинки кварца, яка вирізана паралельно оптичній вісі, щоб падаюче плоско-поляризоване світло виходило поляризованим по колу

(n_e = 1,5533, (см)).

Дано:

Аналіз та розв’язок:

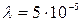см

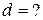
Намалюємо установку для спостереження інтерференції поляризованих променів: П – поляроїд, К – пластинка кварца, і – амплітуда коливань незвичайного і звичайного променів. 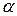– кут між напрямом коливань у падаючому світлі з амплітудою А та одним з головних напрямків пластинки. При інтерференції звичайного та незвичайного променів одержимо еліптичну поляризацію. Рівняння еліпса буде .

Звичайний і незвичайний промені, які пройшли пластинку К, мають різницю ходу, яка дорівнює 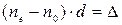і відповідно різницю фаз . Якщо таке, що , тобто , рівняння еліпса буде мати вигляд 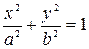, якщо ще й , то і рівняння має вигляд , тобто рівняння кола. Світло буде поляризоване по колу. Для цього 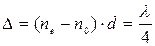, звідси см.

Відповідь: Найменша товщина пластинки см. В загальному виді , де , при , , що ми і використали в задачі.