Квантование магнитного потока

Согласно основным положениям квантовой механики следует, что квантование энергии, заряда, импульса и других физических величин происходит только в микромире и свойственно процессам, протекающим в молекулах, атомах, ядрах.

Изучение явлений, происходящих при температурах, близких к Т = 0 К, показало, что возможно и макроскопическое квантование.

Действительно, экспериментально наблюдается квантование величин, характеризующих свойства макроскопических тел, размеры которых в 10⁵ раз превосходят размеры атомов.

Если электрический ток протекает по сверхпроводящему металлическому кольцу, то он становится незатухающим из-за отсутствия сопротивления и потерь на выделение теплоты Джоуля-Ленца.

Классическая теория природу этого явления объяснить не смогла.

Сверхпроводящее кольцо позволило наблюдать в большом масштабе квантовый эффект.

Сила тока в сверхпроводящем кольце не принимает любые значения и не изменяется непрерывно.

Как и всякий ток, сверхпроводящий ток создает магнитное поле. Квантование тока приводит к квантованию индукции магнитного поля, т. е. она может принимать только ряд дискретных значений, а не любые, как это следует из классической физики.

Это, в свою очередь, приводит к квантованию магнитного потока сквозь сечение сверхпроводящего кольца, т. е.

Ф_м = NФ₀,

где N = 1, 2, 3, ...;

Рис. 14

Ф₀ =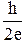

Ф₀ = 2,0678506(54)×10^-15 Вб - квант магнитного потока.

Магнитный поток - макроскопическая величина, и возможность его квантования означает переход к большим, по сравнению с атомными, масштабам квантования.

Экспериментально квант магнитного потока определен на основе эффекта Джозефсона.

При некоторых условиях критический ток через сверхпроводящий контакт оказывается периодически зависящим от внешнего магнитного потока с периодом, равным кванту магнитного потока Ф₀.

Согласно теории сверхпроводимости куперовские электроны, создающие ток (Купера эффект), описываются единой волновой функцией, характеризующейся некоторой фазой j - фазовой когерентностью сверхпроводящих электронов, которая и приводит к квантованию магнитного потока.

В замкнутом сверхпроводящем кольце (рис. 14) разность фаз волновой функции между точками А и В

j_АВ = j_А - j_В,

удовлетворяет соотношению Джозефсона

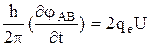, (3)

где U - разность потенциалов между точками А и В контура L (штриховая линия, рис. 14).

Согласно закону электромагнитной индукции напряжение между т. А и В (рис. 1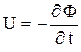4)

, (4)

где Ф - магнитный поток, охваченный контуром L.

Из уравнений (3) и (4 следует, что

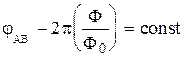. (5)

Постоянная интегрирования в этом выражении связана со скоростью движения сверхпроводящих электронов, что следует из квантово-механического выражения для скорости куперовских пар:

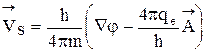, (6)

где m - масса электрона; 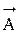- векторный потенциал электромагнитного поля.

Интегрируя 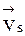по контуру L между точками А и В, получаем следующее выражение:

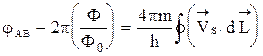. (7)

Фундаментальность явления квантования магнитного потока сказывается, например, в существовании квантовых вихрей в сверхпроводниках II рода, определяющих магнитные свойства большого класса сверхпроводников.

Квантование магнитного потока наряду с эффектом Джозефсона составляет основу работы сверхпроводящих квантовых интерферометров.

В настоящее время ведутся работы по созданию суперкомпьютора нового поколения на основе эффекта Джозефсона.