Приближения слабой и сильной связи. Функция Блоха

Дальнейшее развитие квантовая теория проводимости металлов получила в зонной теории Зоммерфельда.

Согласно этой теории кристаллическое тело рассматривается, как периодическая структура, в которой ионы, расположенные в узлах кристаллической решетки, создают электрическое поле. Для описания поведения электрона в этом поле используются методы приближения сильной и слабой связи. По методу «приближения сильной связи» каждый электрон имеет свою систему дискретных энергетических уровней, а энергия связи электрона с атомами значительно больше их кинетической энергии движения в кристалле. Из-за сильной связи электрона с атомами только внешние (валентные) электроны при сближении атомов на расстояние сравнимое с размерами самих атомов (r » 10^-10 м), переходят от одного атома к другому. Согласно метода «приближения слабой связи» считается, что энергия взаимодействия

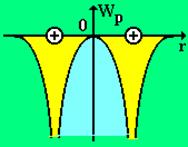Рис. 1

электрона с решеткой много меньше их кинетической энергии, что позволяет считать электроны свободными. Если два изолированных атома находятся на расстоянии много больше их диаметра, то потенциальный барьер для внешних электронов у этих атомов настолько широк, что вероятность просачивания электрона сквозь потенциальный барьер близка к нулю (рис. 1).

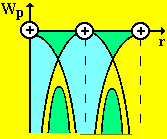Рис. 2

При сближении атомов на расстояние, сравнимое с периодом кристаллической решетки твердого тела происходит перекрытие электрических полей из-за сильного взаимодействия атомов.

Потенциальные кривые накладываются друг на друга (рис. 2), происходит их сужение и понижение. Поэтому получают свободу перемещения по кристаллу не только валентные, но и электроны, расположенные на более глубоких энергетических уровнях, за счет туннельного прохождения сквозь потенциальный барьер, отделяющий соседние атомы друг от друга. Основной задачей теории твердого тела является определение энергетического спектра электронов в кристалле. Для свободного электрона все точки пространства эквивалентны и вероятность его обнаружения в той или иной области этого пространства одинакова и не зависит от координат электрона.

Иначе обстоит дело с электронами, движущимися в периодическом поле правильной кристаллической решетки, образованной ионами, расположенными в ее узлах (рис. 3).

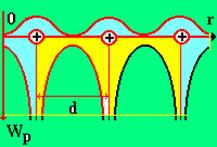Рис. 3

Вероятность обнаружения электрона в данной точке кристалла должна быть периодической функцией координаты, например х. Положения, отличающиеся друг от друга на величину, кратную постоянной решетки d, для электрона являются одинаково вероятными. Различными будут только положения в пределах одного периода.

Следовательно, амплитуда волновой функции электрона y(х), движущегося в периодическом электрическом поле решетки, не остается постоянной, а периодически изменяется (модулирована с периодом, равном d) с течением времени.

Если обозначить амплитуду волновой функции через u(x), то волновую функцию электрона, движущегося в направлении оси Х, можно представить в виде функции Блоха: y(х) = u(x)×e ^{i k x} ,

где е - основание натуральных логарифмов; i = -1; k = 2p / l - волновое число; l - длина волны электрона.

Таким образом, на распределение электронов по энергетическим уровням в твердых телах влияет: 1. внутреннее периодическое электрическое поле ионов кристаллической решетки; 2) взаимодействие между атомами (происходит перекрытие волновых функций валентных электронов).

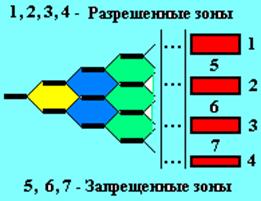Рис. 4

В результате этого влияния происходит объединение энергетических уровней в зоны разрешенных энергий, разделенных запрещенными зонами (рис. 4).

Вывод: При объединении N атомов вещества в кристалл вместо отдельных энергетических уровней, в энергетическом спектре электронов, возникают зоны разрешенных энергий из (2 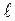+1)N дискретных уровней ( 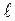- орбитальное квантовое число).

Расстояние между уровнями в разрешенной зоне кристалла очень мало. Например, при ширине разрешенной зоны в 1 эВ (1эВ = 1,6×10^-19 Дж) это расстояние составляет примерно 10^-22 эВ. Но число уровней в разрешенных зонах конечно, что оказывает влияние на распределение электронов по энергетическим состояниям.