Механические и электромеханические характеристики двигателей постоянного тока последовательного возбуждения (ДПТ ПВ).

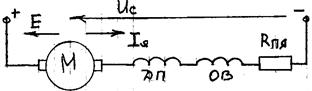
Схема включения:

Обмотки возбуждения ДПТ ПВ включены последовательно с якорем. Поток возбуждения двигателя будет определятся нагрузкой на валу двигателя. Уравнение равновесия напряжения данного двигателя имеет вид U_c=E+I_я(R_z+R_пя+R_ов); Е=КФ(I_я)w.

;

.

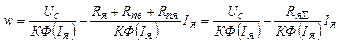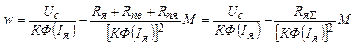Т.е. вид уравнения данного двигателя аналогичен виду ДПТ НВ, но в эти двигатели дополнительно входит сопротивление обмотки возбуждения и, в отличие от двигателя независимого возбуждения, нельзя аналитически в общем виде получить электромеханические скоростные характеристики двигателя, так как поток и ток возбуждения связаны нелинейной зависимостью, которую трудно представить в виде формулы. Для построения электромеханических и механических характеристик необходимо знать зависимости Ф_*(Iя_*) и М_*(Iя_*) , которые были бы универсальными для всей серии двигателей. Эти зависимости существуют, так как внутри одной серии зазоры и степень насыщения машин мало отличаются друг от друга для всех машин.

Приблизительно вид таких зависимостей следующий:

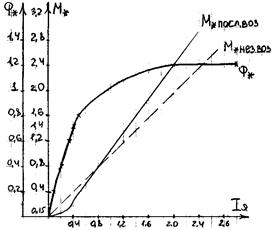
I зона - I_я*£0,3; М_*£0,15;

II зона - I_я*=0,3¸1,3; М_*=0,15¸1,4;

III зона - I_я*>1,3; М_*>1,4.

Следует обратить внимание, что при токе I_я*>1 момент, развиваемый двигателем с последовательным возбуждением, возрастает в большей степени, чем ток М_*>I_я* и эта ситуация является одним из достоинств двигателей с последовательным возбуждением. При одной и той же перегрузке по току двигатели последовательного возбуждения развивают больший момент. Это связанно с тем, что с увеличением тока растет поток двигателя. Так для двигателя независимого возбуждения:

I_я*доп=2¸2,5 - М_*=2,0¸2,5 – НВ

I_я*доп=2¸2,5 - М_*=2,4¸3,0 – ПВ

Зная зависимости Ф_*(I_я*) и М_*(I_я*), можно построить одну зависимость Ф_*(М_*)

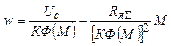
Для полного представления о характеристиках двигателя с последовательным возбуждением пользуются кусочно-линейной аппроксимацией кривой намагничивания Ф(I_я).

1,2 зона: Ф=a₁I_я; М=КФI_я; ; ;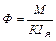

;

.

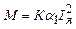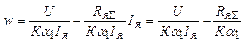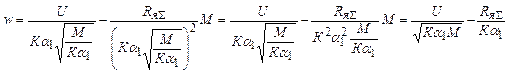3 зона: Ф=Ф₀+a₂I_я

Из выражения скоростных характеристик видно, что они представляют из себя кривые гиперболического вида одной из асимптот, которой является ось ординат, а второй -асимптотой говорить не имеет смысла, так как она соответствует I_я®¥, М®¥, т.е. она лежит вне аппроксимации.

Из выражения электромеханических характеристик видно, что при идеальном холостом ходе, когда ток якоря и момент стремятся к нулю, скорость двигателя w®¥. В действительности при токе якоря равном нулю, есть остаточное магнитное поле Ф_ост*=0,02¸0,09 и наличие остаточного поля беспечивает величину скорости идеального холостого хода . Скорость при этом превышает номинальную скорость в 10 раз, что недопустимо из условия прочности коллектора и бандаже крепящих обмоток якоря.

Следует заметить, что допустимым значением идеального холостого хода для выпускаемых двигателей является w_0*доп<4.

Данные двигатели последовательного возбуждения нельзя применять для механизмов, у которых возможен режим холостого хода с малыми потерями. Эти двигатели запрещается применять для механизмов с использованием цепных, ременных и клиноременных передач.

Наибольшая крутизна электромеханических характеристик в начальной части. Участок линейной аппроксимации в третей зоне обеспечивает более пологую механическую характеристику. На участках большей нагрузки I_я*>2, крутизна электромеханических характеристик практически не зависит от нагрузки. При полюсном насыщении магнитной цепи двигателя уравнение двигателя последовательного возбуждения становится аналогичным что и для двигателей с независимым возбуждением. В этом случае электромеханические характеристики будут представлять из себя прямые линии.