Интегрирующее звено. Подставив в уравнение (1.63) значения b0 = 0 и a0 = a2 = 0, получим уравнение состояния следующего вида (дифференциальное уравнение первого порядка):

Подставив в уравнение (1.63) значения b₀ = 0 и a₀ = a₂ = 0, получим уравнение состояния следующего вида (дифференциальное уравнение первого порядка):

a₁ y′(t) = b₁ x(t) (1.68.)

Выходной параметр звена пропорционален интегралу его входного параметра и описывается следующим выражением:

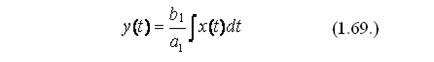
Передаточная функция интегрирующего звена может быть найдена с помощью преобразования по Лапласу и будет иметь вид:

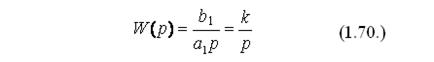
В данном случае k – передаточный коэффициент звена, размерность которого определяется отношением размерности скорости изменения выходного параметра к размерности входного.

Переходная функция звена при х(t) = 1(t) имеет следующее представление:

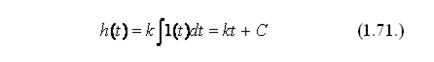
В данном случае С – постоянная интегрирования, при начальных условиях равная нулю.

При постоянном параметре входного воздействия выходной параметр может изменяться, т.к. постоянная интегрирования может принимать различные значения, поэтому интегрирующее звено называют астатическим. Если величина входного параметра

уменьшится до нуля, то, в отличие от пропорционального звена, в интегрирующем звене величина выходного параметра не будет стремиться к нулю.

Интегрирующее звено также называют интегратором. Для получения АФЧХ интегрирующего звена подставим в выражение (1.70.) jwвместо р, и получим:

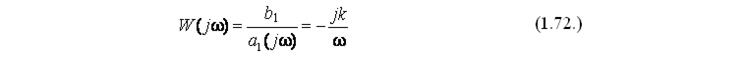
Из выражения видно, что действительная частотная характеристика Re(w) равна нулю, при этом мнимая частотная характеристика совпадет с АЧХ:

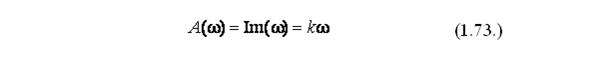
Далее, найдем ФЧХ интегрирующего звена следующим образом:

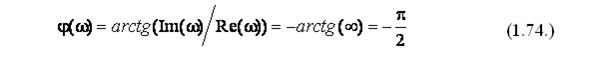
Из этого следует, что интегратор ослабляет высокие частоты и неограниченно усиливает низкие частоты. Амплитуда выходных колебаний стремится к нулюс ростом частоты входных колебаний, при этом сдвиг фаз постоянен и равен – π/2.

Графическое представление характеристик звена изображено на рисунке 30.

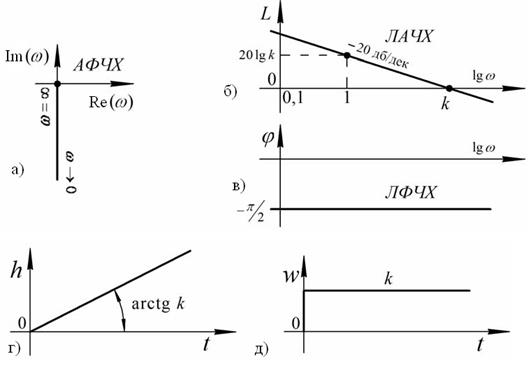
Рис.30. Характеристики интегрирующего звена: а), б), в) – частотные;

г), д), - временные

Существующие реальные интегрирующие звенья характеризуются «накапливанием» входного воздействия и обладают заметной инерционностью.

Интегрирующее звено не может находиться в состоянии равновесия при любом постоянном значении входного сигнала.

При воздействии любой минимальной величины входного параметра, величина выходного параметра через некоторое время может стать

несоизмеримо большой. Положение равновесия в данном звене достигается только при отсутствии входного воздействия.

Примерами существующих звеньев может служить конденсатор (электрическая емкость), гидравлический демпфер и т.д. Схема реального представления интегрирующего звена изображена на рисунке 31.

Рис.31. Реальное представление интегрирующего звена (конденсатора)