Типовые звенья систем управления
Элементарные звенья, из которых состоит система автоматического управления, имеют различные принципы действия и конструктивные особенности. Для удобства проектирования, анализа систем, применяются типовые виды элементарных звеньев, имеющие определенные динамические параметры. Данные звенья соединяют в требуемую структурную схему, и в зависимости от их характеристик получают необходимые выходные параметры системы. Характеристиками звеньев являются дифференциальные уравнения, описывающие процессы, происходящие в звене во время переходного процесса.
Система автоматического управления может состоять из звеньев, использующих различные виды энергии (пар, вода, тепло, ветер, электричество, атомная энергия и т.д.) и различное конструктивное исполнение (электродвигатель, реле, датчики давления, датчики уровня, преобразователи, регуляторы температуры и т.д.). Независимо от перечисленных различий переходные процессы в звеньях могут описываться одними и теми же дифференциальными уравнениями, так как схожие динамические параметры различных звеньев позволяют объединить их в типовые группы. Создание классификации типовых звеньев, выделение типовых групп из их большого количества позволило упростить создание реальных систем автоматического управления, их проектирование и расчет.
Элементарное звено – неделимое звено, имеющее по одному входу и выходу, описываемое дифференциальным уравнением не выше второго порядка и пропускающее сигнал только в одном направлении.
Наиболее удобно классифицировать типовые звенья, используя частные формы линейного дифференциального уравнения второго порядка, представленного ниже:
a0 y′′( t) + a1 y′(t) + a2 y(t) = b0 x′(t) + b1 x(t) (1.63.)
При изменении коэффициентов a и b изменяется уравнение состояния, и в свою очередь изменяется вид (тип) описываемого данным уравнением звена. В таблице изменения характеристик типовых звеньев САУ, в зависимости от изменения коэффициентов дифференциального уравнения, на рисунке 27.1. приведены виды звеньев, реализация которых имеет физический смысл (1.63.).
Представленные звенья имеют общие особенности. Звенья, у которых коэффициенты a2 ≠ 0 и b1 ≠ 0, обладают однозначной связью между входом и выходом в статическом режиме. Поэтому их называют статическимиили позиционными. К этим звеньям относятся звенья, расположенные в таблице под №№ 1, 3, 4, 6, 8 и 9. Звенья под №№ 2, 5, 7 называют астатическими.
Звенья, у которых a2 ≠ 0 и a1 ≠ 0 или a0 ≠ 0 (№ 4, 6, 9) обладают инерционностью (замедлением).
Звенья № 1, 2 и 3 имеют только два коэффициента не равные нулю, поэтому считаются элементарными. Все остальные звенья могут быть образованы из элементарных звеньев путем комбинирования.
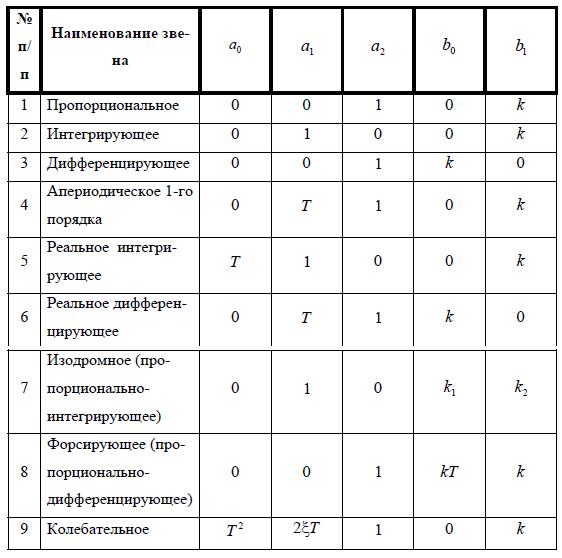
Рис.27.1 Таблица изменения характеристик типовых звеньев САУ, в зависимости от
изменения коэффициентов дифференциального уравнения
Подробнее рассмотрим виды типовых звеньев, т.к. знание их характеристик существенно облегчает анализ и синтез САУ, потому что любой элемент системы и вся система в целом могут быть представлены в виде одного или совокупности типовых звеньев.
1.8.1. Пропорциональное (безынерционное) звено
Подставив в уравнение (1.63) значения bо = 0 и a1 = a2 = 0, получим уравнение состояния следующего вида:

где выходной параметр пропорционален входному. Звено, процессы в котором описываются указанным уравнением состояния, называется пропорциональным
или безынерционным.
Передаточную функцию безынерционного звена можно найти, применив к выражению
(1.64.) прямое преобразование Лапласа. После преобразования получаем:
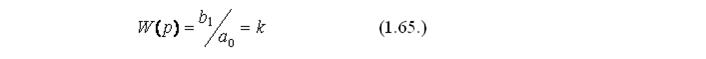
В данном случае k – передаточный коэффициент звена, размерность которого определяется отношением размерности выходного параметра к размерности входного.
Переходная функция звена h(t) имеет следующее представление:

Импульсная переходная характеристика будет выглядеть:
w(t) = h′(t) = kδ (t)(1.67.)
Графическое представление характеристик звена изображено на рисунке 28.

Рис.28. Характеристики пропорционального звена: а), б), в) – частотные;
г), д), - временные.
Пропорциональное (безынерционное) звено можно охарактеризовать равномерным пропусканием всех частот с отсутствием сдвига по фазе. Совпадение по фазе выходных колебаний с входными называют синфазностью.
Реальные звенья все же обладают инерционностью, поэтому относятся к типу пропорциональных (безынерционных) условно, т.к. инерционность звена считается незначительной, если его инерционность пренебрежительно мала относительно инерционности всей системы. К типу таких реальных пропорциональных звеньев могут быть отнесены червячные редукторы, рычажные сочленения, усилители и т.д. Реальное представление пропорционального звена изображено на рисунке 29.
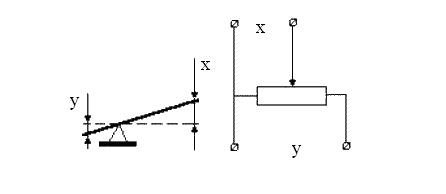
Рис.29. Реальные представления пропорционального (безынерционного) звена
Дата добавления: 2016-02-04; просмотров: 973;
