Частотные характеристики объекта управления
При гармоническом воздействии на входе системы, на ее выходе возникают вынужденные колебания, охарактеризовать которые можно с помощью их частотных характеристик. На рисунке 25 представлено графическое изображение входного и выходного сигналов.
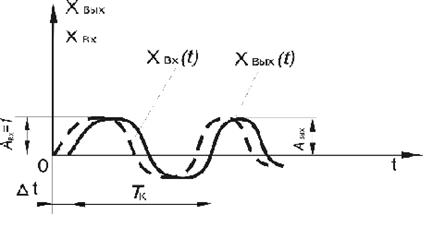
Рис.25. Входной и выходной сигналы гармонических колебаний системы
На графике изображено некоторое гармоническое воздействие, описываемое синусоидой с амплитудой A = const и частотой w, например:
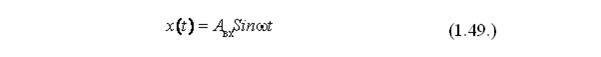
В данном случае Авx=1, поэтому входное воздействие является единичным гармоническим колебанием, в котором угловая частота w = 2p / Тк, период колебаний Тк. В установившемся режиме на выходе системы установились гармонические колебания:

Выходные колебания имеют ту же частоту, что и входные, но изменившуюся амплитуду Ay(w) и сдвиг по фазе относительно входных колебаний на угол j(w), который рассчитывается по временному сдвигу Dt:
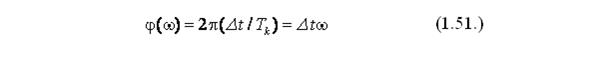
При увеличении частоты колебаний от 0 до ¥, определяя установившиеся амплитуды и фазы выходных колебаний для различных частот, можно установить зависимость от соотношения выходной амплитуды к входной A(w) = Ay(w) /A вх(w) и соотношения сдвига фазы выходных колебаний к входным j(w)= jy(w )- j вx(w). Такие зависимости называются амплитудно-частотными характеристиками A(w) (АЧХ) или фазово-частотными характеристиками j(w) (ФЧХ).
При моделировании и анализе систем автоматического управления используют преобразование Фурье, состоящее в переходе функции от оригинала к изображению. Преобразование Фурье определяется выражением:
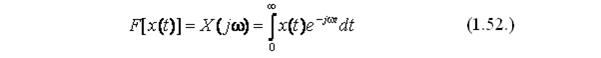
Данное преобразование называется прямым односторонним преобразованием Фурье, получившееся изображение - X(jw)- изображением по Фурье или спектром функции - x(t). Обратное преобразование Фурье состоит в переходе от изображения функции к оригиналу и определяется следующим выражением:
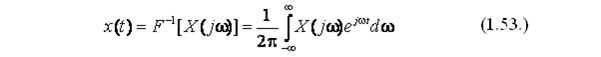
Нетрудно заметить, что преобразование Лапласа (1.16.) и преобразование Фурье (1.52.) идентичны, за исключением символа p у Лапласа и символа jw у Фурье. Широкое применение в теории автоматического управления получило отношение изображений по Фурье выходного ко входному параметру:
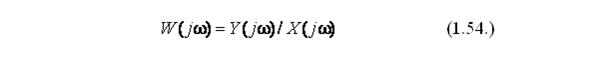
Данное отношение называется частотной передаточной функцией или амплитудно-фазово-частотной характеристикой (АФЧХ). Так как преобразования по Лапласу и Фурье различаются только применяемыми символами p и jw, то к изображениям функций по Фурье применяют такие же операции, как с изображениями по Лапласу, заменяя указанные символы. Выражение амплитудно-фазово-частотной характеристики W(jw) получают из выражения передаточной функции, заменив символы:
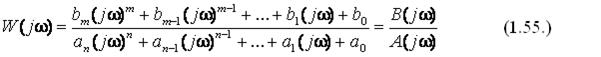
Для представления АФЧХ в алгебраической форме выделяют вещественную Re(jw) и мнимую Im(jw) составляющие:
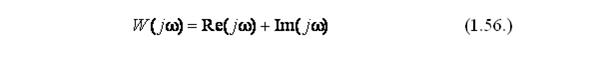
Действительной частотной характеристикой Re(jw) называется зависимость действительной части АФЧХ от частоты, а мнимой частотной характеристикой Im(jw), зависимость мнимой части АФЧХ от частоты. Действительную и мнимую частотные характеристики можно выразить через полиномы числителя и знаменателя выражения (1.14.), выделяя действительную и мнимую часть.
Стандартным методом отображения АФЧХ на комплексной плоскости при изменении частоты от –¥ до +¥ является годограф, представляющий собой кривую, которую описывает конец вектора W(jω), показанный на рисунке 26:
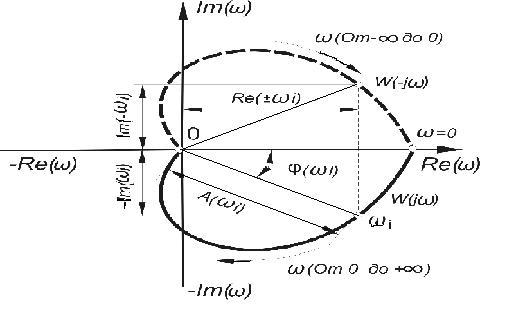
Рис.26. Амплитудно-фазово-частотная характеристика на комплексной плоскости
Параметром на кривой годографа является частота, изменяющаяся от –¥ до +¥, угол j (ωi) – сдвиг по фазе между выходным и входным сигналом, если провести радиус-вектор в любую точку W(jω) для произвольной частоты ωi, он покажет амплитуду выходного сигнала. Подразумевая, что АФЧХ является обобщением обычного коэффициента усиления k и фазового сдвига, в случае их зависимости от частоты, W(jω) называют также комплексным коэффициентом передачи.
В случае необходимости для частотного анализа систем применяется также раздельное построение графиков амплитудно-частотной характеристики (АЧХ) и фазово-частотной характеристики (ФЧХ):
- амплитудная частотная характеристика (АЧХ) – график функции A(ω) = W( jω),
- фазовая частотная характеристика (ФЧХ) – график функции j (ω) = Arg W( jω).
Показательная форма записи АФЧХ имеет следующий вид (1.57.):
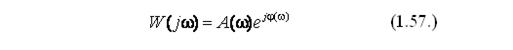
где A(ω) – модуль, а j (ω) – аргумент, представленные в следующем виде:
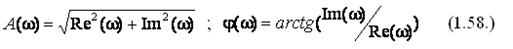
Для наглядности изображения частотных характеристик в большом диапазоне частот на практике нашло широкое применение логарифмического масштаба. Логарифмический масштаб позволяет представлять частотные характеристики отрезками ломаных линий, делать выводы о характеристиках сложных систем с помощью простого суммирования характеристик составляющих звеньев.
Единицей измерения частоты в логарифмическом масштабе является декада. Отношение частот w1 и w2 равно одной декаде, если:
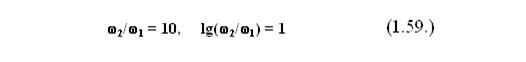
В децибелах выражают отношение амплитуд в логарифмическом масштабе. Мощность w1 больше мощности w2 на один децибел, если соблюдается равенство: 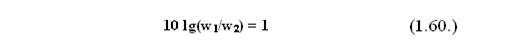
Мощности относятся между собой также, как квадраты образующих их физических величин, поэтому величина a1 больше величины а2 на один децибел, если соблюдается равенство: 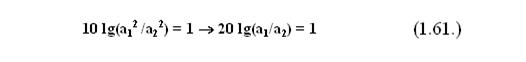
В теории автоматического управления нашло широкое применение использование логарифмических амплитудно-частотных (ЛАЧХ) и фазово-частотных (ЛФЧХ) характеристик. Графики ЛАЧХ и ЛФЧХ изображены на рисунке 27.
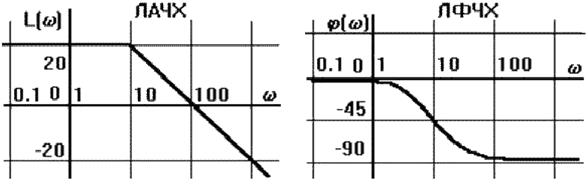
Рис.27. Изображение частотных характеристик в логарифмическом масштабе
ЛАЧХ и ЛФЧХ можно получить путем логарифмирования частотной передаточной функции, получая при этом следующее выражение:
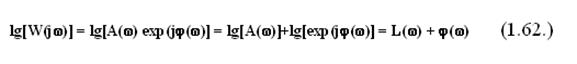
Чтобы получить ЛАЧХ, первое слагаемое умножается на 20, отсюда получим
L(w) = 20 lg A(w). Получившееся значение L(w) откладываем на графике, и получаем изменение уровня сигнала на 20 дБ при изменении частоты сигнала в 10 раз. Единичному промежутку изменения частоты на графике соответствует изменение w в 10 раз.
ЛФЧХ получаем из второго слагаемого, для элементарного звена значение j(w) не превышает: -p ≤ j ≤ p.
Определить параметры системы или звена и восстановить их передаточные функции просто, зная их частотные характеристики.
Дата добавления: 2016-02-04; просмотров: 965;
