Основные классификационные признаки

Системы автоматического управления и системы автоматического регулирования могут классифицироваться по различным признакам. Схема классификации систем приведена на рисунке 12. Различают несколько основных подгрупп классификации:

- по методу управления

- по характеру использования информации

- по результатам работы в установившемся состоянии

- по виду используемой энергии

- по характеру воздействия во времени

- по виду дифференциального управления

Подгруппа систем, различающихся по методу управления, подразделяется на классы неприспосабливающихся (неадаптивных) и приспосабливающихся (адаптивных) систем, в которых класс неприспосабливающихся систем подразделяется на подклассы стабилизирующих, программных и следящих систем, а класс приспосабливающихся систем подразделяется на классы экстремальных и оптимальных систем.

Системы подразделяются на автоматические и автоматизированные.

Автоматические системы работают без участия человека в процессе управления.

Автоматизированные системы работают при частичном участии человека в процессе управления. Данное участие может заключаться в выборе одного решения из множества вариантов.

Неприсбосабливающиеся системы являются одними из самых простых систем автоматического управления, в которых управляющие параметры задаются на основе уже имеющихся данных и обеспечивают устойчивое управление системой с учетом типовых или объективно предполагаемых условий работы.

Стабилизирующие системы – системы, поддерживающие постоянное значение заданного выходного параметра.

Программные системы – системы, обеспечивающие изменение выходного параметра по определенной программе.

Следящие системы – системы, изменяющие выходной параметр в зависимости от внешнего воздействия с заданной на входе точностью, причем значение воздействия изменяется произвольно.

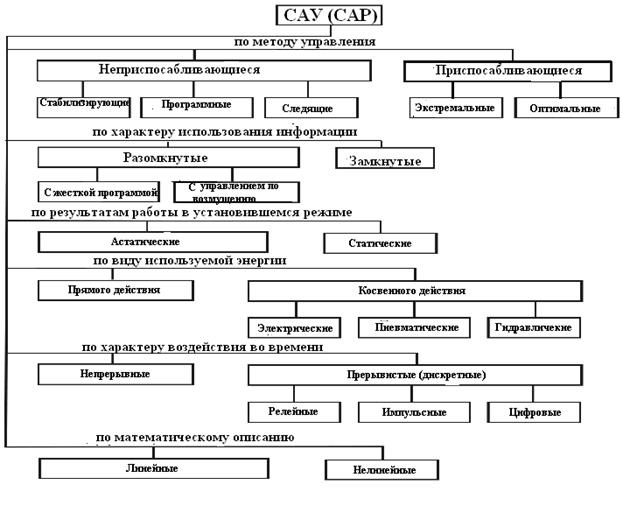
Рис. 12. Классификация САУ и САР

В большинстве систем автоматического управления используется принцип обратной связи, т.е. данные системы являются замкнутыми и управляющие параметры задаются с учетом результата управления.

Положительнаяобратная связь увеличивает значение выходного параметра, отрицательная обратная связь уменьшает значение выходного параметра, по сравнению со значением выходного параметра системы управления без обратной связи. При положительной обратной связи величина параметра обратной связи Х_ос суммируется с входной величиной Х_вх, а при отрицательной обратной связи Х_ос вычитается из входной величины Х_вх. Значит, для входного параметра объекта управления системы с обратной связью, верно равенство:

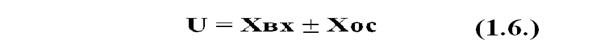Исходя из вышесказанного, величиной входного параметра объекта управления будет являться отклонение регулируемого параметра от его заданной величины U, а выходным параметром Y – управляющий параметр.

В простой замкнутой системе автоматического управления (рисунок 9) на вход сравнивающего корректирующего устройства (СКУ) поступает заданная задающим устройством величина параметра Х_вх и измеренное датчиком и преобразованное преобразователем в сигнал значение ошибки (отклонения) управления Х_ос. Учитывая знак ошибки, (СКУ) корректирует и выдает на выходе (СКУ) параметр U. Величина U поступает на вход объекта управления (ОУ), на выходе которого преобразуется в управляющий параметр Y, с целью придания системе нужного состояния (преодоления отклонения, вызванного внешним возмущением), а значит, в процессе работы системы параметр Y пытается приблизиться к значению Х_вх – параметру заданному оператором. Процесс работы такой системы сводится к преодолению отклонения системы от заданного состояния, поэтому такие системы автоматического управления называются системами с регулированием по отклонению. Участие человека заключается в установлении величины параметра задающего устройства, а само решение задачи управления, заключающееся в устранении отклонения фактического значения выходного параметра системы от заданного, выполняется автоматически.

Разомкнутые системы управления применяются в тех случаях, когда известны параметры внешнего возмущения, реакция объекта управления на данное возмущение, имеются типовые схемы и алгоритмы применения разомкнутых систем в нужных

условиях, т.к. применение разомкнутой системы дешевле, чем замкнутой, и они применяются, когда это не влияет на качество выполнения поставленной задачи.

Исполнительные органы систем разомкнутого типа обычно имеют жесткие электромеханические характеристики, встречающиеся, например, у синхронных машин, шаговых двигателей. Кроме замкнутых и разомкнутых систем применяются также комбинированные системы.

Достоинства разомкнутых систем:

- простота

- низкая стоимость

Недостатки разомкнутых систем:

- отсутствует корректировка входного параметра

- не учитывается влияние воздействия случайного внешнего возмущения

- не учитывается состояние системы в процессе работы

По количеству регулируемых параметров системы автоматического управления подразделяются на одномерные и многомерные.

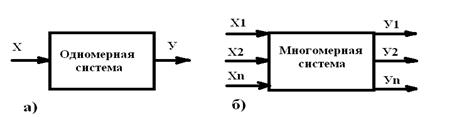
Рис. 13. Структурные схемы: а) одномерной системы, б) многомерной системы

Структурные схемы данных систем представлены на рисунке 13, где Х (Х₁, Х₂, …, Х_n) – величины заданных параметров, У (У₁, У₂, …, У_n) – величины управляющих параметров.

К одномерным системам можно отнести регуляторы Ползунова, Уатта, т.к. в них регулируется только один параметр, в регуляторе Ползунова – уровень, в регуляторе Уатта – скорость вращения вала.

В настоящее время большинство систем автоматического управления являются многомерными, потому что управляют несколькими параметрами. В многомерных системах могут быть задействованы несколько каналов управления. Каждый параметр характеризуется своим управляющим воздействием, действующим через определенный канал и имеющим свой управляющий элемент, причем каналы и управляющие элементы не взаимодействуют друг с другом и косвенное влияние случайных возмущений, создаваемых каналами, крайне мало, поэтому, обычно не учитывается. Такую многомерную систему можно представить, как множество одномерных систем со своими управляющими элементами.

Однако, многомерные системы также характеризуются наличием связей между управляемыми параметрами. Связи могут быть внутренними и внешними.

Внутренние связи зависят от физических характеристик системы, тогда как внешние – от зависимостей между отдельными управляемыми параметрами.

Системы могут различаться по принципу представления информации на аналоговые (непрерывные) и дискретные. В непрерывных системах входные и управляющие

параметры зависят от времени (непрерывно изменяются с течением времени), т.е. непрерывно с изменением величины входного параметра изменяется и величина управляющего воздействия. В дискретных системах автоматического управления входные и управляющие параметры изменяются с учетом дискретизации, т.е. прерывисто или пошагово, в определенные временные промежутки.

Непрерывные системы подразделяются на линейные и нелинейные, но если в системе из множества звеньев, имеется одно нелинейное звено, то вся система считается нелинейной.

Линейные системы – системы, процессы в которых описываются линейными дифференциальными уравнениями. Из-за сложности описания процессов, происходящих в системах, линейными дифференциальными уравнениями, их линеаризуют, т.е. приводят к линейному виду с помощью определенных ограничений и допусков

Нелинейные системы – системы, процессы в которых описываются нелинейными дифференциальными уравнениями.

Дискретные системы подразделяются на:

- релейные

- импульсные
- цифровые

Релейные системы характеризуются наличием звена (звеньев) с релейной характеристикой, т.е. когда величина выходного параметра данного звена изменяется скачкообразно при определенной величине входного параметра.

Импульсные системы характеризуются наличием звена (звеньев) с импульсной характеристикой, т.е. когда при непрерывном изменении величины входного параметра, величина выходного параметра изменяется только в определенные промежутки времени.

Цифровые системы характеризуются наличием цифровых устройств, в которых сигналы (входные и выходные параметры) являются дискретизированными по уровню и по времени.

Различают системы с сосредоточенными и системы с распределенными параметрами.

Системами с сосредоточенными параметрами называются системы, характеризующиеся величиной управляемого параметра в одной точке пространства, в которых величина управляемого параметра является только временной функцией.

Системами с распределенными параметрами называются системы, характеризующиеся величиной управляемого параметра в нескольких точках пространства.