Полное внутреннее отражение
Элементы геометрической оптики
Принцип Гюйгенса
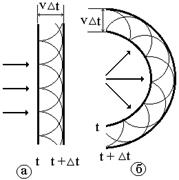 Рис. 7.1
Рис. 7.1
|
При распространении волн в среде, в том числе и электромагнитных, для нахождения нового фронта волны в любой момент времени используют принцип Гюйгенса.
Каждая точка фронта волны является источником вторичных волн.
В однородной изотропной среде волновые поверхности вторичных волн имеют вид сфер радиуса v×Dt, где v - cкорость распространения волны в среде. Проводя огибающую волновых фронтов вторичных волн, получаем новый фронт волны в данный момент времени (рис. 7.1, а, б).
Закон отражения
Используя принцип Гюйгенса можно доказать закон отражения электромагнитных волн на границе раздела двух диэлектриков.
Угол падения равен углу отражения. Лучи, падающий и отраженный, вместе с перпендикуляром к границе раздела двух диэлектриков, лежат в одной плоскости. Ð a = Ð b. (7.1)
Пусть на плоскую границу СД раздела двух сред падает плоская световая волна (лучи 1 и 2, рис. 7.2). Угол a между лучом и перпендикуляром к СД называют углом падения. Если в данный момент времени фронт падающей волны ОВ достигает т. О, то согласно принципу Гюйгенса эта точка
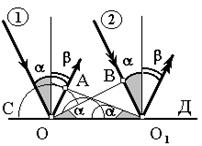 Рис. 7.2
Рис. 7.2
|
начинает излучать вторичную волну. За время Dt = ВО1/v падающий луч 2 достигает т. О1. За это же время фронт вторичной волны, после отражения в т. О, распространяясь в той же среде, достигает точек полусферы, радиусом ОА = v Dt = BO1.Новый фронт волны изображен плоскостью АО1, а направление распространения - лучом ОА. Угол b называют углом отражения. Из равенства треугольников ОАО1 и ОВО1 следует закон отражения: угол падения равен углу отражения.
Закон преломления
Оптически однородная среда 1 характеризуется абсолютным показателем преломления 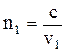 , (7.2)
, (7.2)
где с - скорость света в вакууме; v1 - cкорость света в первой среде.
Среда 2 характеризуется абсолютным показателем преломления
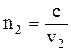 , (7.3)
, (7.3)
где v2 - скорость света во второй среде.
Отношение n2 / n1 = n21 (7.4)
называют относительным показателем преломления второй среды относительно первой.
Для прозрачных диэлектриков, у которых m = 1, используя теорию Максвелла, или 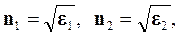 (7.5)
(7.5)
где e1, e2 - диэлектрические проницаемости первой и второй сред.
Для вакуума n = 1.
Из-за дисперсии (частоты света n » 1014 Гц), например, для воды n =1,33, а не n = 9 (e = 81), как это следует из электродинамики для малых частот. Если скорость распространения света в первой среде v1, а во второй - v2,
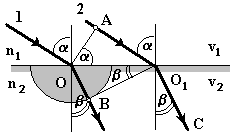 Рис. 7.3
Рис. 7.3
|
то за время Dt прохождения падающей плоской волной расстояния АО1 в первой среде АО1 = v1Dt. Фронт вторичной волны, возбуждаемый во второй среде (в соответствии с принципом Гюйгенса), достигает точек полусферы, радиус которой ОВ = v2Dt. Новый фронт волны, распространяемой во второй среде, изображается плоскостью ВО1 (рис. 7.3), а направление ее распространения - лучами ОВ и О1С (перпендикулярными к фронту волны). Угол b между лучом ОВ и нормалью к границе раздела двух диэлектриков в точке О называют углом преломления. Из треугольников ОАО1 и ОВО1 следует, что АО1 = ОО1 sin a, OB = OO1 sin b.
Их отношение и выражает закон преломления (закон Снеллиуса):
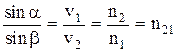 . (7.6)
. (7.6)
Отношение синуса угла падения к синусу угла преломления равно относительному показателю преломления двух сред.
Полное внутреннее отражение
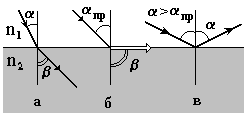 Рис. 7.4
Рис. 7.4
|
Согласно закону преломления на границе раздела двух сред можно наблюдать полное внутреннее отражение, если n1 > n2, т. е. Ðb >Ða (рис. 7.4). Следовательно, существует такой предельный угол падения Ðaпр, когда Ðb = 900. Тогда закон преломления (7.6) принимает следующий вид:
sin aпр = 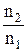 , (sin 900=1) (7.7)
, (sin 900=1) (7.7)
При дальнейшем увеличении угла падения Ða > Ðaпр свет полностью отражается от границы раздела двух сред.
Такое явление называют полным внутренним отражением и широкоиспользуют в оптике, например, для изменения направления световых лучей (рис. 7. 5, а, б).
Применяется в телескопах, биноклях, волоконной оптике и других оптических приборах.
В классических волновых процессах, таких, как явление полного внутреннего отражения электромагнитных волн, наблюдаются явления, аналогичные туннельному эффекту в квантовой механике, что связано с корпускулярно-волновыми свойствами частиц.
Действительно, при переходе света из одной среды в другую наблюдается преломление света, связанное с изменением скорости его распространения в различных средах. На границе раздела двух сред луч света разделяется на два: преломленный и отраженный.
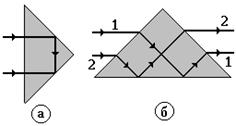 Рис. 7.5
Рис. 7.5
|
Согласно закону преломления имеем, что если n1 > n2, то при Ða > Ðaпр наблюдается полное внутреннее отражение. Почему это происходит? Решение уравнений Максвелла показывает, что интенсивность света во второй среде отлична от нуля, но очень быстро, по экспоненте, затухает при удалении от границы раздела.
Экспериментальная схема по наблюдению полного внутреннего отражения приведена на рис. 7.6, демонстрирует явление проникновения света в область, «запрещенную», геометрической оптикой.
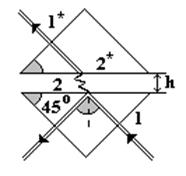 Рис. 7.6
Рис. 7.6
|
На грань 1 прямоугольной равнобедренной стеклянной призмы перпендикулярно падает луч света и, не преломляясь падает на грань 2, наблюдается полное внутреннее отражение, так как угол падения (Ða = 450) луча на грань 2 больше предельного угла полного внутреннего отражения (для стекла n2 = 1,5; Ðaпр = 420).
Если на некотором расстоянии H ~ l/2 от грани 2 поместить такую же призму, то луч света пройдет через грань 2* и выйдет из призмы через грань 1* параллельно лучу, падавшему на грань 1. Интенсивность J прошедшего светового потока экспоненциально убывает с увеличением промежутка h между призмами по закону:
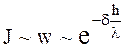 ,
,
где w - некоторая вероятность прохождения луча во вторую среду; d - коэффициент, зависящий от показателя преломления вещества; l - длина волны падающего света
Следовательно, проникновение света в «запрещенную» область представляет собой оптическую аналогию квантового туннельного эффекта.
Явление полного внутреннего отражения действительно является полным, так как при этом отражается вся энергия падающего света на границу раздела двух сред, чем при отражении, например, от поверхности металлических зеркал. Используя это явление можно проследить еще одну аналогию между преломлением и отражением света, с одной стороны, и излучением Вавилова-Черенкова, с другой стороны.
ИНТЕРФЕРЕНЦИЯ ВОЛН
7.2.1. Роль векторов 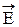 и
и 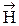
На практике в реальных средах могут распространяться одновременно несколько волн. В результате сложения волн наблюдается ряд интересных явлений: интерференция, дифракция, отражение и преломление волн и т. д.
Эти волновые явления характерны не только для механических волн, но и электрических, магнитных, световых и т. д. Волновые свойства проявляют и все элементарные частицы, что было доказано квантовой механикой.
Одно из интереснейших волновых явлений, которое наблюдается при распространении в среде двух и более волн, получило название интерференции. Оптически однородная среда 1 характеризуется абсолютным показателем преломления 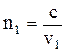 , (7.8)
, (7.8)
где с - скорость света в вакууме; v1 - cкорость света в первой среде.
Среда 2 характеризуется абсолютным показателем преломления
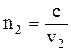 , (7.9)
, (7.9)
где v2 - скорость света во второй среде.
Отношение 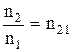 (7.10)
(7.10)
называют относительным показателем преломления второй среды относительно первой. Для прозрачных диэлектриков, у которых m = 1, используя теорию Максвелла, или
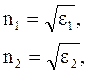 (7.11)
(7.11)
где e1, e2 - диэлектрические проницаемости первой и второй сред.
Для вакуума n = 1. Из-за дисперсии (частоты света n » 1014 Гц), например, для воды n =1,33, а не n = 9 (e = 81), как это следует из электродинамики для малых частот. Свет - электромагнитные волны. Поэтому электромагнитное поле определяется векторами 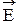 и
и 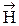 , характеризующими напряженности электрического и магнитного полей cоответственно. Однако во многих процессах взаимодействия света с веществом, например, таких, как воздействие света на органы зрения, фотоэлементы и другие приборы, определяющая роль принадлежит вектору
, характеризующими напряженности электрического и магнитного полей cоответственно. Однако во многих процессах взаимодействия света с веществом, например, таких, как воздействие света на органы зрения, фотоэлементы и другие приборы, определяющая роль принадлежит вектору 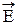 , который в оптике называют световым вектором.
, который в оптике называют световым вектором.
Все процессы, происходящие в приборах под влиянием света, вызваны действием электромагнитного поля световой волны на заряженные частицы, входящие в состав атомов и молекул. В данных процессах основную роль играют электроны из-за большой частоты колебаний светового вектора (n~10 15 Гц). Сила Лоренца F, действующая на электрон со стороны электромагнитного поля,
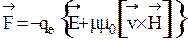 , (7.12)
, (7.12)
где qe - заряд электрона; v - его скорость; m - магнитная проницаемость окружающей среды; m0 - магнитная постоянная.
Максимальное значение модуля векторного произведения второго слагаемого при  , с учетом mm0Н2 = ee0Е2,
, с учетом mm0Н2 = ee0Е2,
получается mm0Н×vэ = 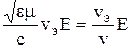 , (7.13)
, (7.13)
где 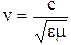 ;
; 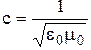
- скорости света в веществе и в вакууме соответственно; e0 -электрическая постоянная; e - диэлектрическая проницаемость вещества.
Причем v >>vэ, так как скорость света в веществе v~108 м/c, a скорость электрона в атоме vэ~106 м/c. Известно, что
v = w×Ra,
где w = 2pn - циклическая частота; Ra~10-10 м - размер атома, играет роль амплитуды вынужденных колебаний электрона в атоме.
Следовательно, 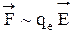 , и основную роль играет вектор
, и основную роль играет вектор 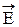 , а не вектор
, а не вектор 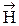 . Полученные результаты хорошо согласуются с данными опытов.
. Полученные результаты хорошо согласуются с данными опытов.
Например, в опытах Винера области почернения фотоэмульсии под действием света совпадают с пучностями электрического вектора 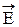 .
.
Дата добавления: 2016-02-04; просмотров: 3390;
